CIENCIAS EXACTAS Y NATURALES-Artículo Científico

CORRELACIÓN CANÓNICA ENTRE ÍNDICES MACROCLIMÁTICOS Y VARIABLES METEOROLÓGICAS DE SUPERFICIE EN COLOMBIA

CANONICAL CORRELATION BETWEEN LARGE SCALE CLIMATE OSCILLATIONS AND SURFACE METEOROLOGICAL VARIABLES IN COLOMBIA

Diana Díaz¹, Nancy Villegas²

¹ Física, M.Sc., Meteorología, Departamento de Ciencias Básicas. Universidad de Bogotá Jorge Tadeo Lozano, carrera 4 # 22-61, Bogotá, D.C., Colombia. e-mail: dianac.diaz@utadeo.edu.co

² Ingeniera Oceanóloga, Ph.D. en Ciencias Físicas y Matemáticas, Departamento de Geociencias. Universidad Nacional, Avenida Carrera 30 # 45, Bogotá D.C., Colombia. e- mail: nlvillegasb@unal.edu.co

Rev. U.D.C.A Act. & Div. Cient. 18(2): 543-552, Julio-Diciembre, 2015

RESUMEN

El análisis de correlación canónica es propuesto como herramienta para relacionar variables meteorológicas de superficie en Colombia y oscilaciones climáticas, de gran escala. El trabajo aporta una metodología, que permite generar conocimientos sobre el clima y mejorar los pronósticos, a largo y mediano plazo. El estudio fue realizado para El Niño Oscilación Sur (ENSO), la Oscilación del Atlántico Norte (NAO), la Oscilación Cuasibienal (QBO) y los valores totales mensuales de precipitación y de temperatura máxima. Las oscilaciones fueron representadas por medio de índices climáticos globales y las variables utilizadas corresponden a tres estaciones meteorológicas, ubicadas en los departamentos de Santander y de Boyacá. Los resultados muestran la potencia de este método estadístico para identificar asociaciones, mediante un enfoque multivariado, donde los índices macroclimáticos actúan como predictores. Las correlaciones y las cargas canónicas encontradas indican una correspondencia, entre las variables y el ciclo ENSO, especialmente, durante diciembrefebrero, en el periodo 1980-2012. Por el contrario, la relación con la NAO y la QBO, es discreta y oscilante.

Palabras clave: Variabilidad climática, análisis multivariante, oscilaciones atmosféricas, El Niño/Oscilación del Sur (ENOS).

SUMMARY

This study examines relationships between available surface meteorology variables and climatic oscillations using canonical correlation analysis (CCA). The general methodology is explained and applied to three particular cases. Canonical loadings and cross loadings from CCA are evaluated for three meteorological stations located in municipalities of Boyacá and Santander. The tests were carry out using temperature and precipitation data and three climate oscillations the Ocean Niño Index (ONI), North Atlantic Oscillation (NAO), and Quasi-biennial oscillation (QBO). The results show the power of this statistical method to identify associations with an acceptable level of confidence using multivariate approach. The analysis reveals relationships mostly between the variables and the ENSO for all cases and a discrete connection with the NAO and QBO. Add climate indices to the group of independent variables increased the explained variance rates between 3 and 7% and therefore contribute to a better understanding of climate dynamics in the country.

Key words: Climate variability, atmospheric oscillations, Multivariate analysis, El Niño Southern Oscillation (ENSO).

INTRODUCCIÓN

El clima de Colombia está determinado por la ubicación del país sobre el ecuador geográfico, zona donde confluyen los vientos alisios (Carmona & Poveda, 2012). Adicionalmente, la cercanía con el océano pacífico, el mar caribe, la selva amazónica y la presencia de la cordillera de los Andes, favorecen los procesos convectivos, que hacen de Colombia un país con abundancia hídrica y diversidad de climas (IDEAM, 2005). Los procesos océano-atmosféricos de mayor influencia en Colombia son el desplazamiento de la Zona de Convergencia Intertropical (ZCIT), el fenómeno del Niño Oscilación Sur (ENSO) y la Oscilación Madden Julian (OMJ)(IDEAM, 2005; Poveda et al. 2011; Henríquez, 2012; Hoyos et al . 2013). Las características promedio y la clasificación de los climas en cada región son conocidas gracias a los registros históricos de las variables meteorológicas de superficie (VMS); sin embargo, dada la complejidad del sistema climático, aún no se ha comprendido completamente la influencia de las Oscilaciones Climáticas de Gran Escala (OCGE) sobre el comportamiento de las VMS, en las diferentes zonas climáticas del país (Montealegre, 2009; Henríquez, 2012). El desconocimiento de dicha relación no favorece la realización de pronósticos a largo y mediano plazo y aumenta el grado de vulnerabilidad de las regiones, ante situaciones meteorológicas adversas.

Comprender cómo afectan las OCGE a la región tropical contribuye a una mejor comprensión del clima global y a la realización de mejores pronósticos (Vera et al. 2010; Fonseca & Cavalcanti, 2012). El problema principal para adelantar este tipo de investigaciones radica en la poca disponibilidad de series de tiempo, cuya longitud permita estudiar fluctuaciones interdecadales e interanuales. A pesar de la dificultad, varios autores han intentado evaluar la influencia de fenómenos macroclimáticos, en los patrones climáticos locales; algunos ejemplos son: el estudio de la Oscilación del Atlántico Norte (NAO), por Poveda et al . (1998, 2002); la Oscilación Cuasibienal (QBO), por Zea et al . (2000); Zuluaga et al . (2000) y Carmona & Poveda (2012) y el fenómeno El Niño Oscilación del Sur (ENOS), por Montealegre (2009), Poveda et al . (2011), Henríquez (2012), Hoyos et al . (2013) y Córdoba et al . (2014), entre otros. Tanto los anteriores autores como el presente estudio evalúan el efecto de la NAO, la QBO y el ENOS, por medio de índices, que describen el proceso físico correspondiente.

El índice para representar la NAO es definido como la diferencia normalizada entre la presión, a nivel del mar en Gibraltar y Reykjavik, al suroeste de Islandia. Un índice positivo significa una realza en la Alta de los Azores, ocasionando, en el hemisferio norte, un ascenso atípico en la temperatura del aire, cuando es invierno y, un descenso, cuando es verano. Un índice negativo implica el proceso contrario (Zorita et al. 1991). Poveda et al. (1998, 2002) realizaron correlaciones cruzadas trimestrales, entre la NAO y la precipitación, encontrando asociaciones fuertes y negativas, especialmente, en el sector de la costa atlántica y más débiles y positivas, hacia el centro y sur del país, con un rezago de seis meses; sin embargo, los mismos autores recomiendan profundizar en el tema.

El índice para representar la QBO es la dirección del viento zonal, en el nivel de 30 hPa. La fluctuación en la dirección del viento es observada en la baja y media estratósfera ecuatorial, con un período entre 20 a 36 meses y una media de 26 meses. Algunos estudios indican que afecta la frecuencia de los ciclones tropicales en el Atlántico y las condiciones climáticas del país (Zea et al. 2000; Baldwin et al. 2001). Zuluaga et al . (2000) correlacionaron la QBO con la precipitación y la radiación de onda larga de varios sectores del país, sin obtener asociación estadística, razón por la cual, los autores sugieren emplear otros métodos de correlación. A pesar de la existencia de una banda cuasi-bienal en los registros de lluvia en el país, aún son pocos los trabajos publicados sobre el posible vínculo, entre la QBO y la hidrología del país.

Finalmente, los índices Southern Oscillation Index (SOI) y Ocean Niño Index (ONI) son considerados para representar el ENOS (Poveda et al . 1998; 2002; 2011). El SOI es calculado como la diferencia estandarizada de presión, a nivel del mar, entre Tahití y Darwin; valores positivos, se asocian con eventos La Niña y negativos, con El Niño (Stevens & Ruscher, 2014). El ONI, se calcula como la media móvil trimestral de las anomalías de la TSM, medida por ERSST.v3b en la región Niño 3.4, sobre la base de períodos de treinta años, actualizados cada cinco años. Valores por encima de 0,5 por tres meses consecutivos, se vinculan con eventos Niño e inferiores a -0,5, a eventos Niña. Los estudios de correlación cruzada trimestral, entre el ENOS y la hidroclimatología del país, han identificado asociaciones con la precipitación y con los caudales de los ríos; las más fuertes, durante el trimestre diciembre-enero-febrero (DEF) y las más débiles, para el periodo marzo-abril-mayo (MAM) (Poveda et al. 2002). Estos estudios revelan que el impacto del ENOS sobre las variables hidrológicas, se propaga del oeste hacia el este (Poveda et al. 2002; 2011; Hoyos et al. 2013; Córdoba et al . 2014). A diferencia de los estudios mencionados, este trabajo propone el uso de correlación canónica entre índices macroclimáticos, como el SOI, ONI, NAO o QBO y VMS, como la temperatura máxima y la precipitación en los ejemplos construidos.

Análisis de Correlación Canónica (ACC): El ACC es un método multivariado lineal utilizado para comparar dos conjuntos de datos: uno independiente X y otro dependiente Y, compuestos de un número p de variables x_i y q variables y_i , respectivamente.

En el ACC, se crean combinaciones lineales x* y y*, llamadas variables canónicas (VC), con al menos dos de las variables de cada conjunto:

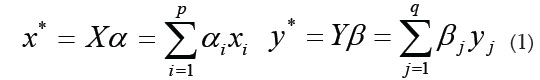
Los vectores α y β deben maximizar la correlación entre x* e y*; cada VC debe tener varianza y no estar correlacionada con otras VC:

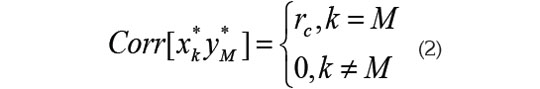
Donde rc es la correlación canónica. El cálculo de las VC, se realiza a partir de las matrices de varianza y de covarianza[ S c ] de las variables iniciales X y Y:

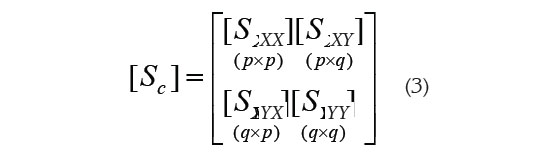
[S _xx] y [S _yy] son las matrices de varianza y covarianza de las p variables en X y las q variables en Y; [S_xy] [S_yx] son las matrices de covarianza entre los elementos de X y los de Y. Las correlaciones canónicas r_c entre las diferentes VC, que se determinen, están dadas por la raíz cuadrada de los valores propios, diferentes de cero de las matrices:

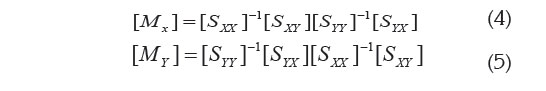
y los vectores canónicos α y β serán los respectivos vectores propios de las matrices que satisfacen:

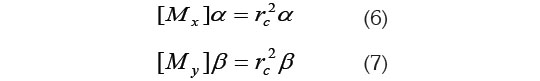
Los valores de α y β revelan cuáles variables tienen la mayor fuerza explicativa dentro de la correlación y son importantes cuando se está construyendo un modelo predictivo (Wilks, 2006; Singh et al. 2012). Además de α y β en el ACC, se calculan también las cargas canónicas (CC) y las cargas canónicas cruzadas (CCC). Las CC permiten conocer la contribución de cada variable observada i x y i y a su respectiva VC x* y y* . Las CC independientes son las correlaciones lineales entre i x y x* , y las CC dependientes entre i y y y* . Las CCC proveen información más significativa de la relación entre las variables observadas y las nuevas VC (Katz et al. 2003). Las CCC independientes son las correlaciones lineales entre i x y y* y las CCC dependientes entre i y y x* . Finalmente, en el ACC es estimado el coeficiente de redundancia, que permite establecer el porcentaje de varianza, explicada en el conjunto de variables dependientes, por parte del conjunto de variables independientes (Katz et al. 2003). El ACC fue el método seleccionado, por ser uno de los menos dependientes de la periodicidad de los fenómenos y, como en este caso se están analizando procesos que evolucionan en escalas de tiempo distintas, utilizar esta metodología, es apropiado (Wilks, 2006; Singh et al. 2012).

MATERIALES Y MÉTODOS

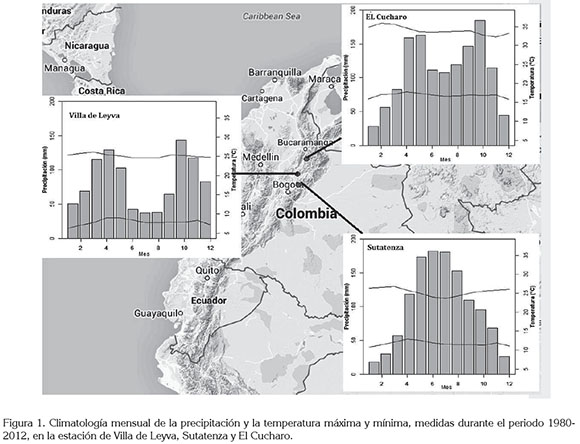
El estudio implementa el ACC como herramienta para relacionar los índices de la NAO, el ENOS y la QBO con la precipitación y la temperatura máxima de tres estaciones meteorológicas, cada una ubicada en El Cucharo, departamento de Santander, Villa de Leyva y Sutatenza, departamento de Boyacá, como se muestra en la figura 1. Las VMS fueron obtenidas del Instituto de Estudios Ambientales (IDEAM), mediante el convenio marco No. 031/2009. Las estaciones meteorológicas fueron elegidas por contar con series mensuales multianuales, mayores de 30 años, en ambas variables y por tener el menor número de datos faltantes, durante el periodo 1980-2012. Las series de los índices fueron obtenidas del sitio web del Earth System Research Laboratory (ESRL, 2014), también para el periodo 1980-2012.

Las variables fueron organizadas como series de tiempo trimestrales, correspondientes a los periodos: diciembre-enero- febrero (DEF), marzo-abril-mayo (MAM), junio-julio-agosto (JJA) y septiembre-octubre-noviembre (SON), es decir, que cada serie original se divide en cuatro series, de acuerdo con Stevens & Ruscher (2014); esta forma de disponer los datos maximiza la posibilidad de encontrar relaciones entre las OCGE y las VMS.

El ACC fue realizado por separado para cada trimestre; el grupo de las variables dependientes y_t fue conformado por las series de precipitación y de temperatura máxima de cada trimestre analizado. El grupo de las variables independientes X_t estuvo compuesto por las series de los índices de todos los trimestres, es decir, que en cada análisis fue evaluado el grado de relación de las VMS de un trimestre dado, con los índices de todos los trimestres del año.

Para los tres lugares fueron realizadas tres pruebas distintas, por cada uno de los cuatro trimestres. En la primera prueba, las variables independientes fueron NAO y ONI; en la segunda, NAO y SOI y, en la tercera, NAO, ONI y QBO. El objetivo de realizar tres pruebas distintas fue identificar con qué combinación de índices se obtenía la mayor correlación; por tanto, se realizaron en total 36 ACC.

Al finalizar cada ACC fue realizada la prueba F con la aproximación de Rao (Stevens & Ruscher, 2014) y se aceptaron los resultados estadísticamente significativos, con un nivel de confianza, al menos del 90% (Hair et al. 1998). En cada análisis, se estimaron los siguientes valores: los coeficientes de correlación entre las variables canónicas ( r_c ), los vectores α y β , las cargas canónicas (CC), las cargas canónicas cruzadas (CCC), los coeficientes de redundancia y los porcentajes de confiabilidad. No existe un estándar universal de significancia para considerar las correlaciones y las cargas canónicas, obtenidas de un ACC, por tanto, el investigador debe interpretar los resultados, de acuerdo a la naturaleza de la investigación y a su propia experiencia. Para el presente estudio, se consideraron relevantes valores iguales o superiores a 0,4, en el caso de las CC y a 0,2, para las CCC, que son los umbrales usuales para el ACC, con datos geofísicos (Zorita et al . 1991; Stevens & Ruscher, 2014).

En la etapa siguiente fueron graficadas las cargas, en un diagrama de barras. Las CC dependientes fueron multiplicadas con las CCC independientes y este valor es el graficado. De acuerdo con lo explicado en la introducción, en este caso, las CC dependientes son las correlaciones lineales entre la precipitación y la temperatura con su correspondiente variable canónica. Y las CCC independientes son la correlación lineal entre los índices considerados y las variables canónicas, resultantes de la combinación lineal de la precipitación y la temperatura. Multiplicar estas dos cargas permite identifica el grado de relación entre cada índice y las variables mencionadas. Para este trabajo fue escrito un código en R versión 2.14.2, que permite ejecutar todos los pasos mencionados. El código fue escrito para calcular los estadísticos descriptivos, graficar las variables, construir las series trimestrales, realizar los ACC, seleccionar los valores, de acuerdo a los umbrales establecidos y visualizar los resultados, mediante la gráfica de barras. La ventaja del código es que automatiza la ejecución del análisis y agiliza la posterior emulación para cualquier serie de variables meteorológicas.

RESULTADOS Y DISCUSIÓN

Climatología del área de estudio: La figura 1 muestra el comportamiento medio mensual multianual de la precipitación y la temperatura máxima y mínima de los lugares considerados. En el sector de la estación Villa de Leyva, la precipitación presenta un régimen bimodal con dos máximos, que ocurren durante abril y octubre y mínimos, en enero y junio-agosto, que corresponden con el desplazamiento surnorte de la ZCIT; este punto recibe en promedio 992 mm/ año. La temperatura promedio es de 17°C, con los valores promedio mensuales más bajos, durante noviembre-enero y los más altos, en marzo-mayo. La temperatura máxima varía alrededor de los 25°C y la mínima de los 7°C. En el sector de la estación Sutatenza, la precipitación es máxima durante junio-julio y mínima, diciembre-enero; este punto recibe en promedio 1209,71mm/año. La temperatura promedio es de 17,82°C y los valores más bajos son registrados durante junio-agosto y los más altos, en noviembre-marzo. La temperatura máxima varía alrededor de los 25°C y la mínima de los 11°C.

En el sector de El Cucharo, la precipitación es máxima durante abril-mayo y septiembre-octubre y mínima, en diciembre-febrero y junio-julio; este punto recibe en promedio 1328,5 mm/año. La temperatura promedio en este sector es de 24,74°C y los valores más bajos son registrados durante octubre-noviembre y los más altos, en febrero-marzo. La temperatura máxima oscila alrededor de los 33°C y la mínima de los 16°C. Considerando los climagramas de la figura 1, el patrón pluviométrico de Villa de Leyva y El Cucharo están determinados por el doble paso de la ZCIT durante el año, que ocasiona dos temporadas secas y dos húmedas durante el año. Por el contrario, en Sutatenza es observada una temporada seca, predominante de noviembre a marzo y otra húmeda, de abril a octubre.

Análisis de Correlación: En la primera prueba, la proporción de varianza de las variables meteorológicas, explicada por los índices, oscila entre 16 y 43%, en el periodo DEF; entre 18 y 30%, en MAM; entre 19 y 26%, en JJA y entre 24 y 33%, durante la temporada SON, como es resumido en la tabla 1. El trimestre con los porcentajes más altos es DEF, seguido por SON. Los menores coeficientes de correlación y de porcentajes de varianza explicada fueron obtenidos en el caso de Sutatenza y los mayores, en Villa de Leyva. La diferencia de los resultados obtenidos en estos dos casos es explicada por el contraste del ciclo hidrológico, entre los dos lugares. En Sutatenza, el régimen de precipitación es controlado, primordialmente, por procesos de mesoescala, como la circulación valle-montaña; por el contrario, en Villa de Leyva y El Cucharo, el patrón de lluvia es bimodal, en respuesta, principalmente, al desplazamiento de la ZCIT. La discrepancia entre los factores generadores de la precipitación de los tres lugares, explica la disimilitud en la influencia de las OCGE sobre el comportamiento de las VMS, siendo más visible la relación en el caso de Villa de Leyva y El Cucharo.

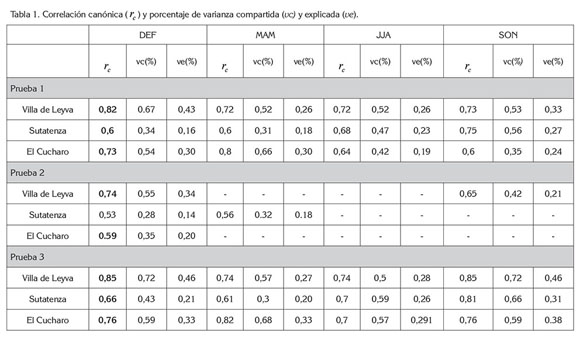
En la figura 2, los números junto a la etiqueta de los índices son utilizados para referirse al periodo: 1, corresponde a DEF; 2, a MAM; 3, a JJA, y 4, a SON. La figura mostró que durante DEF sobresalen las correlaciones de las variables ONI1, ONI3 y NAO1. En MAM, la temperatura máxima esta mejor relacionada con ONI1, ONI3 y con NAO1 y NAO2; la asociación de la precipitación con todos los índices no superó el límite propuesto de 0,4 y, por esta razón, no hay barras en esta variable, durante MAM. En JJA, no se presenta asociación con la temperatura máxima, pero hay correlaciones menores e inversas con todos los índices y la precipitación. En SON sobresalen las relaciones con ONI3 y ONI4. En resumen, los valores más altos de las cargas ocurren entre el ONI y las VMS de DEF y los más bajos, entre la NAO y las VMS, de todos los trimestres.

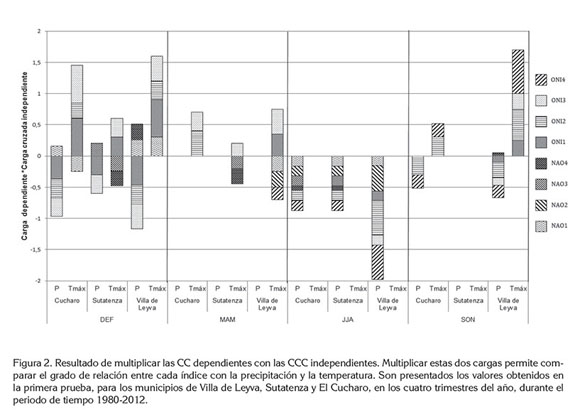
Analizando el caso de Villa de Leyva, la relación entre el ONI y la temperatura máxima es positiva durante todos los trimestres, excepto en JJA, cuando las cargas canónicas están por debajo del umbral de 0,4. La relación con la precipitación es negativa, a excepción del periodo MAM. Para El Cucharo, el sentido de las correlaciones es el mismo que en Villa de Leyva. En Sutatenza continúa el mismo sentido de dependencia, pero con cargas de menor peso.

Los resultados de la primera prueba, para el índice ENOS, están de acuerdo con lo planteado por Poveda et al . (1998; 2002; 2011), quienes obtuvieron las mayores correlaciones cruzadas significativas entre este índice y las variables hidrológicas del trimestre DEF; además, aseguran que MAM es la época menos afectada por eventos ENOS. En cuanto al índice ONI, el sentido de las relaciones corresponde con el fenómeno físico, pues un ONI positivo asociado a eventos Niño está relacionado con una disminución en la precipitación y un ascenso de la temperatura máxima. Sucede también, que la relación entre el ONI y las VMS, se evidencia, incluso, con tres y seis meses de rezago. Esto corresponde al hecho de que la señal del ENOS se propaga de occidente a oriente y tarda en su recorrido, a través del pacífico ecuatorial, aproximadamente seis meses; también así lo reportan estudios en Argentina (Barreiro et al . 2014) y Venezuela (Paredes & Guevara, 2013), donde hay regiones con rezagos hasta de siete meses o más y casos en Centroamérica (Alfaro, 2011) y Chile (Cortés et al . 2011), donde la respuesta de las VMS, se evidencia en menor tiempo, por estar sobre la costa pacífica.

Los resultados están de acuerdo, además, con los análisis realizados por Ramírez & Jaramillo (2009), quienes muestran la relación inversa entre el ONI y la precipitación en la región central del país. La diferencia en la altura de las barras de la figura 2 muestra que el impacto de los eventos ENOS varía de un lugar a otro; los trabajos de Montealegre (2009) y Arango et al. (2014a; 2014b), también evidencian que el grado de afectación varía en función de la ubicación geográfica.

En cuanto a la NAO, en muy pocos casos, las cargas canónicas superaron el umbral preestablecido, aunque discreta, se obtiene una relación directa con la precipitación durante SON y DEF e inversa, durante JJA, para los tres lugares, es decir, que en SON-DEF, si la NAO es positiva, es de esperar un ligero incremento en los niveles de lluvia, pero durante JJA, la relación es contraria. Un comportamiento similar obtuvieron Stevens & Ruscher (2014), quienes reportan que la influencia de la NAO sobre las VMS cambia de sentido, según la época del año y Montealegre (2009), quien concluyó, que las correlaciones con la NAO no siguen un patrón definido. La relación entre la NAO y las VMS, se puede entender, teniendo en cuenta que la NAO afecta la intensidad de los alisios de noreste y, por consiguiente, el desplazamiento de la ZCIT sobre el atlántico tropical, modificando el transporte de humedad desde el atlántico tropical hacia el continente americano y la actividad convectiva (Poveda et al . 1998), aunque el efecto de la NAO, en la banda interanual sobre la precipitación, parece ser limitado, como Paegle & Mo (2002) y Montealegre (2009), también lo reportaron.

En la segunda prueba, los resultados fueron similares a los de la primera, ya que solo cambió el índice SOI por el ONI y ambos son una forma de representar el mismo fenómeno; sin embargo, como fue observado en la tabla 1, solo en algunos casos los ACC superaron el umbral del 90%, impuesto como límite de fiabilidad; por esta razón, no fueron presentados los gráficos de barras de la prueba. La variabilidad de las VMS estudiadas esta mejor relacionada con la serie ONI, porque el ONI es calculado como una media móvil trimestral, que suaviza la serie y, además, la temperatura superficial del mar, al ser una variable oceánica, tiene mayor inercia, mientras que el SOI es calculado en función de la presión atmosférica, cuya señal es más inestable.

En la tercera prueba, la proporción de varianza -explicada de las variables meteorológicas por parte de los índices-, fue ligeramente mayor, al incluir la QBO en el grupo de las variables independientes. Los valores oscilaron entre 21 y 46%, en el periodo DEF; entre 20 y 33%, en MAM; entre 26 y 29%, en JJA y entre 31 y 46%, durante la temporada. Los porcentajes más altos corresponden el trimestre DEF-SON (Tabla 1). En esta misma prueba, el gráfico obtenido fue idéntico al de la figura 2; la oscilación climática que presentó mayor relación con las variables fue el ONI. En todos los casos, la relación fue directa con la temperatura máxima e indirecta con la precipitación, de los cuatro trimestres, siendo de mayor peso durante DEF y SON. En cuanto a la NAO, las cargas canónicas tuvieron el mismo sentido que en la primera prueba, aunque fueron menores en magnitud. La única diferencia con la primera prueba fue la señal de la QBO, que apareció ligeramente relacionada con los datos de precipitación de El Cucharo y Sutatenza, en todos los trimestres, salvo durante DEF; la relación fue directa con las temperaturas e inversa con la precipitación. Esta relación adicional, que aparece entre las series y la QBO, explica el ligero aumento entre el 3 y el 7% de la varianza, explicada por las oscilaciones climáticas. La QBO alcanza su mayor amplitud en la estratosfera; la hipótesis más aceptada es que su existencia se asocia con el desplazamiento ecuatorial de las ondas kelvin y Rossbygravedad. La QBO es relacionada con la frecuencia de los ciclones en el Atlántico o con el ciclo ENOS, de manera que es posible observar su señal en las VMS, en Colombia. Hasta el momento, Montealegre (2009) y Carmona & Poveda (2012) han identificado señales de periodo similar al de la QBO en las anomalías de precipitación, acumulada durante abril.

La importancia de este trabajo radica en que los resultados encontrados, mediante el ACC, son coherentes con los procesos físicos y con estudios previos de correlación, realizados con cada índice por separado. Esto implica, que el método es una alternativa para identificar relaciones simultáneas, aprovechando el enfoque multivariado de predictores, como lo sugieren Singh et al . (2012). Las correlaciones canónicas obtenidas no son muy grandes, debido a que la varianza explicada por las oscilaciones climáticas en las VMS es generalmente pequeña (Stevens & Ruscher, 2014). Los análisis presentados son un ejemplo para ser extendido a otras regiones del país, con registros meteorológicos mayores a 30 años, incluyendo otros índices, no considerados en el presente estudio.

El trabajo muestra que el ACC permite identificar asociaciones, mediante un enfoque multivariado de índices macroclimáticos, como predictores, dada la coherencia de los resultados encontrados con los procesos físicos y con estudios preliminares de correlación. En general, los resultados de las tres pruebas indican que la variabilidad de las VMS analizadas está asociada, en mayor grado, con el índice ONI. La relación es inversa con la precipitación y directa con la temperatura máxima; las mayores correlaciones ocurren con las series meteorológicas del trimestre DEF y las más débiles, durante MAM. Por ahora, solo se puede afirmar que por medio del ACC, se aprecia una relación lineal conjunta, entre los índices y las series meteorológicas en estudio, donde el mayor peso lo aporta el ONI, seguido de la NAO y una contribución más discreta de la QBO.

Conflicto de intereses: Los autores del presente trabajo declaramos que no existe conflicto de intereses que ponga en riesgo la validez de los resultados obtenidos. Financiación: El proyecto fue financiado por Colciencias, a través de la Convocatoria Nacional para Estudios de Doctorados en Colombia 528.

BIBLIOGRAFÍA

1. ALFARO, E.J. 2011. Uso del análisis de correlación canónica para la predicción de la precipitación pluvial en Centroamérica. Rev. Ing. Competitividad. (Colombia). 9(2):49-58.

2. ARANGO, C.; DORADO, J.; GUZMÁN, D.; RUIZ, J.F. 2014a. Informe análisis compuesto según el índice ENSO ONI, para la temperatura media trimestral de Colombia. IDEAM. Disponible desde Internet en: http://institucional.ideam.gov.co/jsp/2456 (con acceso 20/10/2014).

3. ARANGO, C.; DORADO, J.; GUZMÁN, D.; RUIZ, J.F. 2014b. Variabilidad climática de la precipitación en Colombia asociada al Ciclo El Niño, la Niña - Oscilación del Sur (ENSO). IDEAM. Disponible desde Internet en: http://institucional.ideam.gov.co/jsp/2456 (con acceso 20/10/2014).

4. BALDWIN, M.P.; GRAY, L.J.; DUNKERTON, T.J. 2001. The Quasi-Biennial Oscillation. Rev. Geophys. (Estados Unidos). 39(2):179-229.

5. BARREIRO, M.; DÍAZ, N.; RENOM, M. 2014. Role of the global oceans and land-atmosphere interaction on summertime interdecadal variability over northern Argentina. Climate Dynamics. (Alemania) .42(7-8):1733-1753.

6. CARMONA, A.; POVEDA, G. 2012. Application of hilberthuang transform to detect hydroclimatic variability modes in Colombia. DYNA. 79(175):72-80.

7. CÓRDOBA-MACHADO, S.; PALOMINO-LEMUS, R.; GÁMIZ-FORTIS, S.R.; CASTRO-DÍEZ, Y.; ESTEBAN PARRA, M.J. 2014. Influence of tropical Pacific SST on seasonal precipitation in Colombia: prediction using El Niño and El Niño Modoki. Climate Dynamics. DOI: 10.1007/s00382-014-2232-3.

8. CORTÉS, G.; VARGAS, X.; CPHEE, J. 2011. Climatic sensitivity of streamflow timing in the extratropical western Andes Cordillera. J. Hydrology. (New Zealand). 405(1):93-109.

9. EARTH SYSTEM RESEARCH LABORATORY -ESRL-. 2014. Climate Indices: Monthly Atmospheric and Ocean Time Series Database [online]. National Oceanic and Atmospheric Administration, Boulder (CO. USA). Disponible desde Internet en: http://www.esrl.noaa.gov/psd/data/climateindices/list/ (con acceso 20/10/2014).

10. FONSECA, I.; CAVALCANTI, A. 2012. Large scale and synoptic features associated with extreme precipitation over South America: A review and case studies for the first decade of the 21st century. Atmosph. Res. (Países Bajos). 118:27-40.

11. HAIR, J.F.; ANDERSON, R.E.; TATHAM, R.L.; BLACK, W.C. 1998. Canonical correlation analysis. Multivariate Data Analysis, fifth ed. Prentice Hall. (Estados Unidos). 29p.

12. HENRÍQUEZ, M. 2012. Climatología ambiental de Colombia. Editor Universidad Santo Tomás, Bogotá (Colombia). 330p.

13. HOYOS, N.; ESCOBAR, J.; RESTREPO, J.C.; ARANGO, A.M.; ORTIZ, J.C. 2013. Impact of the 2010-2011 La Niña phenomenon in Colombia, South America: The human toll of an extreme weather event. Applied Geography. (Países Bajos). 39:16-25.

14 IDEAM, 2005. Atlas Climatológico de Colombia. Imprenta Nacional de Colombia. 219p.

15. KATZ, R.W.; PARLANGE, M.B.; TEBALDI, C. 2003. Stochastic modelling of the effects of large-scale circulation on daily weather in the southeastern US. Clim. Change. (Países Bajos). 60:189-216.

16. MONTEALEGRE, J.E. 2009. Estudio de la variabilidad climática de la precipitación en Colombia asociada a procesos oceánicos y atmosféricos de meso y gran escala. Disponible desde Internet en: http://institucional.ideam.gov.co/jsp/812 (con acceso 01/11/2014).

17. PAEGLE, J.N.; MO, K.C. 2002. Linkages between summer rainfall variability over South America and sea surface temperature anomalies. J. Clim. (Estados Unidos). 15(12):1389-1407.

18. PAREDES, F.J.; GUEVARA, E. 2013. A probabilistic model for the prediction of meteorological droughts in Venezuela. Atmósfera. (México). 26(3): 311-323.

19. POVEDA, G.; VÉLEZ, J.; MESA, O.; HOYOS, C.; SALAZAR, L.; MEJÍA, J.; BARCO, O.; CORREA, P. 2002. Influencia de fenómenos macroclimáticos sobre el ciclo anual de la hidrología colombiana: cuantificación lineal, no lineal y percentiles probabilísticos. Meteorol. Colomb. (Colombia). 6:121-130.

20. POVEDA, G.; ÁLVAREZ, D.M.; RUEDA, O.A. 2011. Hydro-climatic variability over the Andes of Colombia associated with ENSO: A review of climatic processes and their impact on one of the Earth's most important biodiversity hotspots. Climate Dynamics. 36(11-12):2233-2249.

21. POVEDA, G.; GIL, M.; QUICENO, N. 1998. El ciclo anual de la Hidrología de Colombia en relación con el ENSO y la NAO. Bull. Inst. fr. Études Andines. (Francia). 27(3):721-731.

22. RAMÍREZ, V.H.; JARAMILLO, A. 2009. Relación entre el índice Oceánico del EL Niño y la lluvia en la región andina central de Colombia. Cenicafe. (Colombia). 60(2):161-172.

23. SINGH, A.; ACHARYA, N.; MOHANTY, U.C.; MISHRA, G. 2012. Performance of Multi Model Canonical Correlation Analysis (MMCCA) for prediction of Indian summer monsoon rainfall using GCMs output. Computes Rendus Geosc. (Francia). 345(2):62-72.

24. STEVENS, K.; RUSCHER, P.H. 2014. Large scale climate oscillations and mesoscale surface meteorological variability in the Apalachicola Chattahoochee-Flint River Basin. J. Hydrology. 517:700-714.

25. VERA, C.; BARANGE, M.; DUBE, O.P.; GODDARD, L.; GRIGGS, D.; KOBYSHEVA, N.; ODADA, E.; TRENBERTH, K. 2010. Needs assessment for climate information on decadal timescales and longer. Procedia Environm. Sci. (Países Bajos). 1(1):275-286.

26. WILKS, D.S. 2006. Statistical Methods in the Atmospheric Sciences, second ed. International Geophysics Series, vol. 59. Academic Press, 464p.

27. ZEA, J.A.; LEÓN, G.E.; ESLAVA, J.A. 2000. La oscilación cuasibienal y algunas relaciones con los eventos cálidos y fríos del pacifico. Meteorol. Colomb. 1:51-58.

28. ZORITA, E.; KHARIN, V.; STORCH, H.V. 1991. The atmospheric circulation and sea surface temperature in the North Atlantic area in winter: their interaction and relevance for Iberian Precipitation. J. Clim. 5:1097-1107.

29. ZULUAGA, M.D.; POSADA , J.E.; POVEDA, G. 2000.Relación entre las fases de la Oscilación Cuasibienal (QBO), la precipitación mensual y la radiación de onda emergente en Colombia. Disponibles desde Internet en: http://www.bdigital.unal.edu.co/4416/1/AA3318 (con acceso 01/11/2014).

Recibido: Noviembre 19 de 2014 Aceptado: Julio 23 de 2015