CIENCIAS EXACTAS Y NATURALES-Artículo Científico

ESTIMACIÓN DE LA CAPACIDAD EN RESTAURANTES DE FABRICACIÓN MASIVA

MEASURING CAPACITY IN MASSIVE PRODUCTION RESTAURANTS

Juan Pablo Orejuela¹, Marco Antonio Salcedo², Luis Eduardo Giraldo³

¹ M.Sc., Profesor asociado Escuela de Ingeniería Industrial. Universidad del Valle, Colombia, calle 13 No 100-00; edificio 357 oficina: 2007-3, Cali, Valle del Cauca, Colombia, e-mail: juan.orejuela@correounivalle.edu.co

² Ing. Industrial, Escuela de Ingeniería Industrial. Universidad del Valle, Colombia, calle 56 N No. 3 an - 46 Cali, Valle del Cauca, Colombia, e-mail:marcoasalcedo@gmail.com

³ Ing. Industrial, Escuela de Ingeniería Industrial. Universidad del Valle, Colombia. Calle 1^a No. 18-16 Cali, Valle del Cauca, e-mail: luised_903@hotmail.com

Rev. U.D.C.A Act. & Div. Cient. 19(1): 219-226, Enero-Junio, 2016

RESUMEN

A pesar que la identificación de la capacidad productiva es de vital importancia en los sistemas productivos y aunque existen estudios desarrollados en diversos sectores, tanto de producción como de servicio, es escasa la investigación referente a la identificación de la capacidad en restaurantes de fabricación masiva, que involucran producción y servicio al cliente, al mismo tiempo. En este artículo, se desarrolló una metodología para determinar la capacidad en estos restaurantes, asociada a un conjunto de menús denominados ''menú tipo''. En la metodología, se presentó -de manera esquemática-, las actividades a realizar y se validó la propuesta; para la agrupación de almuerzos, se utilizó la técnica de clustering; al final, la capacidad es determinada haciendo uso de un modelo de programación lineal. Se encontró que el tiempo de servicio en barra y el tiempo de consumo del almuerzo son los factores que más afectan la capacidad del restaurante.

Palabras clave: Capacidad de servicio, capacidad productiva, planeación de la capacidad, modelación matemática.

SUMMARY

Despite the identification of the productive capacity in productive systems is vitally important to identify the productive capacity, however, although there are several related studies in various sectors of both production and service, the research on the identification of manufacturing capacity in mass production restaurants with production and customer service simultaneously is scarce. In This article a methodology for measuring capacity in these restaurants is developed, which is associated with a set of menus called ''Menu type''. The activities to be carried in the methodology are presented schematically and the proposal methodology is validated. The clustering technique was used for grouping lunch and a linear programming model determines the capacity. It is founded that the bar service time and the launch consumption time are the factors that most affect the restaurant capacity.

Key words: Service capacity, productive capacity, massive production restaurant.

INTRODUCCIÓN

En todas las organizaciones es importante conocer la capacidad del sistema de producción, ya que permite y facilita la toma de decisiones en el corto y largo plazo. Cuando una organización conoce cuáles son las variables críticas de dicho sistema, puede llegar a decidir con contundencia si realiza o no inversiones, que permitan mejoras en sus medidas de desempeño.

Por lo anterior, la capacidad se puede considerar como una variable crítica dentro del sistema de producción, puesto que una inadecuada previsión de la capacidad ocasiona excesos o subutilización de los recursos, lo que incrementa costos, como: de almacenamiento, de oportunidad, de distribución y gastos de administración, elementos que dificultarán el cumplimiento de los objetivos de las organizaciones (Domínguez et al. 1995).

A nivel industrial, el problema de medición de la capacidad se presenta, tanto en los sistemas productivos como en los sistemas de servicios; sin embargo, la definición de la medida de capacidad en servicios es más compleja de realizar, debido a que, normalmente, en estas compañías no se entregan productos tangibles, lo que hace que sea de gran importancia conocer la capacidad que se tiene para prestar el servicio determinado (Wollmann et al. 1995).

Para la medición de la capacidad existe una amplia variedad de conceptos que se pueden emplear, cada uno entregando un resultado diferente, lo que deja ver la complejidad de esta tarea, ya que no existe una medida general o norma genérica para establecerla (Domínguez et al. 1995); por ejemplo, para el caso de los restaurantes de fabricación masiva, la capacidad puede ser medida a partir de las entradas (libras de arroz procesadas por día) o, a partir de las salidas (número de almuerzos por día), lo que importa es que sea una medida estable, es decir, que no requiera revisiones constantes, que puedan afectar, en cualquier caso, las disponibilidades y los planes de capacidad; debe ser representativa del factor productivo, así como de los productos que incorpora y, por último, debe ser adecuada a su objeto: permitir el cálculo de la capacidad disponible de la instalación y compararla con la carga necesaria.

Algunos trabajos de medición y de control de la capacidad en producción, se pueden ver en Martínez et al. (2014); Hung et al. (2013); Ho & Fang (2013); Kumru (2011); Wuttipornpun & Yenradee (2007); Vlachos et al. (2007) y Kalenatic (2001), donde el problema de la capacidad viene integrado con el problema de la planeación y el control de la producción. En la mayoría de estudios, se enfocan al sector de la manufactura, mientras que el sector de servicios ha sido poco abordado y, en menor medida, los sistemas mixtos (producción y servicios).

Algunas de las investigaciones relacionadas a los servicios abordan diversos campos, como la educación, la salud y la alimentación, pero, en este último, no se han identificado -en la revisión-, metodologías exactas, para determinar la capacidad. En una de estas investigaciones, Manyoma et al. (2011) proponen una metodología para medir la capacidad en un programa académico, mediante el uso de la programación lineal, con lo que se determina la capacidad que presentan los recursos y la que consumen los usuarios; al final, se relacionan ambos datos, para determinar la capacidad instalada del programa académico.

Kurz (2016) trata el problema de planeación de capacidad en sistemas job shop, más claramente, proveedores de servicio de mantenimiento, con lead times definidos. Emplean técnicas de optimización analítica e iterativa para, lo cual, el sistema es modelado como una red de colas; mediante tal estudio encuentran que la gestión colaborativa del mantenimiento y las mejoras en los tasas de servicio y gestión de la demanda repercuten positivamente en la capacidad de producción y el costo total.

Heching & Squillante (2014) desarrollaron un enfoque de solución de optimización estocástica de dos fases, aplicado al problema de colas, en sistemas de servicio, como las industrias de servicio de tecnologías de información, para que ellas usen -de manera eficiente y efectiva-, la gestión de capacidad y el proceso de planeación; mediante una gran variedad de experimentos, se sustenta los significativos beneficios del enfoque desarrollado.

Corominas et al. (2010) presentan las cuentas de tiempo de trabajo (WTAs), como una forma de lograr una capacidad de producción flexible, a través de la organización del tiempo de trabajo; también plantean modelos de programación lineal, para planear el tiempo de trabajo en empresas de servicio, los cuales, se prueban computacionalmente, presentado buenos tiempos de solución, para problemas de tamaño razonable.

Otra propuesta es la de Pengfei et al. (2010), quienes utilizan un meta-modelo paramétrico, que busca satisfacer la prestación del servicio en hospitales, dada una situación de desastre por terremoto. Esta propuesta, se centra en predecir la capacidad transitoria, de manera oportuna, en varios hospitales dentro de la zona donde haya ocurrido el desastre; otra investigación en hospitales, se puede ver en Akcali et al. (2006).

Lagemann & Meier (2014) tratan el problema de la planificación de recursos para sistema industriales de productos-servicios, los cuales, experimentan faltas de soporte en la decisión, en cuanto a la planificación de la capacidad se re- fiere, por lo que los autores emplean la simulación para la identificación de los factores más importantes del sistema, para luego determinar el mejor plan de capacidad.

Hwang et al. (2010) abordan el problema de gestión de la demanda y de la capacidad en un restaurante con modelos de optimización, basado en colas, con el que pueden capturar los cambios de la demanda y evaluar, empíricamente, los rendimientos relativos de las estrategias más usadas en restaurantes; con lo anterior, encontraron que un balance entre costo y calidad pueden generar máximos beneficios.

En la revisión realizada, se identificó que el problema de planeación de la capacidad en servicios juega un papel importante en el cumplimiento de los objetivos de estas organizaciones; se evidencia, que indicadores, como el costo, los benéficos, la flexibilidad, la reducción de pérdidas, la eficiencia y la efectividad, se ven afectados por la gestión de la capacidad; sin embargo, para la gestión de la capacidad es importante contar con una correcta estimación de la misma, donde los autores presentan diferentes estrategias para medir y gestionar y emplean la simulación, la optimización, la teoría de colas y los meta-meta moleos, lo que da una idea de la complejidad del problema y de los diferentes que pueden ser estos y sus soluciones, según el sector de aplicación.

En esta investigación, se presenta una metodología para determinar la capacidad de producción en un restaurante, teniendo en cuenta que es un sistema de producción mixto, ya que se centra en la producción masiva por día y combina el servicio con la manufactura, características que lo hace un sistema particular y poco tratado en la bibliografía. La estrategia, se enfoca en la medición de la capacidad desde los recursos disponibles, basándose en un modelo de optimización.

MATERIALES Y MÉTODOS

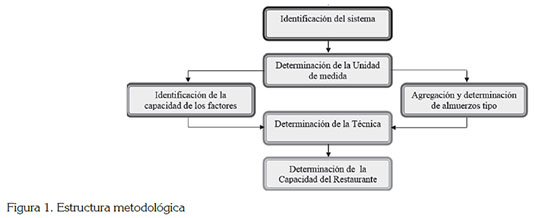
Para determinar la capacidad de producción en un restaurante de producción masiva, se proponen la siguiente estructura metodológica compuesta por cinco etapas (Figura 1).

Etapa 1 -Identificación del sistema y sus factores-: Esta etapa implica la definición del estado actual del sistema productivo dentro del restaurante y se debe apoyar en fuentes primarias y secundarias; se busca recolectar información sobre los factores claves en la estimación de la capacidad: demanda histórica, requerimientos de capacidad, cantidad de materias primas en almacén, tiempos de alistamiento de máquinas, tiempo de consumo, número de mesas disponibles, rutas que siguen las materias primas fundamentales del proceso, cantidad de operarios y turnos de trabajo, máquinas involucradas en el proceso productivo, cantidades de stock de materias primas, producto en proceso y producto terminado.

Etapa 2 -Determinación de la medida de capacidad-: Se toman en consideración las características de cada uno de los factores anteriores, de lo cual, se identifica que plantear la unidad de medida en función de las salidas, dificulta el proceso de medición de la capacidad, ya que este sistema tiene múltiples productos, por tanto, se propone hacerlo sobre la base los recursos. De acuerdo con ello, se plantea el tiempo como unidad de medida de la capacidad, dado que con él se pueden representar las demás unidades y permite la comparación entre los distintos factores del sistema.

Etapa 3 -Identificación de la capacidad de los factores pro- ductivos-: En esta etapa, se analiza la capacidad instalada de los recursos y la capacidad de la maquinaria cuando trabajan en conjunto, dentro del sistema. Este análisis toma en cuenta los mantenimientos preventivos, los tiempos de alistamiento, las precedencias, los turnos de trabajo y limpiezas; con esta información, se calcula la capacidad, teniendo en cuenta los factores de utilización, de eficiencia y de capacidad instalada de cada recurso.

Etapa 4 -Determinación del conjunto de almuerzos tipo y de sus necesidades de capacidad-: Debido a la cantidad de menús que se manejan en este tipo de restaurantes y si se tiene presente que la carga de capacidad del sistema se ve afectada por cada menú que se vaya a preparar, es necesario hacer una agrupación, de acuerdo a la familiaridad de características; al menú representativo de cada uno de estas agrupaciones, se denominó almuerzo tipo. Para la determinación de los almuerzos tipo, se desarrolla un análisis de agrupamientos, por el método de Conglomerados o Clústeres (Peña, 2003), debido a que por este método se pueden agrupar los elementos, de acuerdo a las características que presenten.

Después de tener las clasificaciones, se procede a determinar un menú representativo de cada clase, a través de una función de distancia, en donde el menú con la distancia más corta al centro de masa de cada clase, se establece como el menú representante de esa clase.

Etapa 5 -Optimización del sistema-: En esta etapa, se propone un modelo matemático de programación Lineal, que busca optimizar la cantidad de almuerzos que se sirven durante el tiempo de servicio. El modelo es definido para determinar la capacidad de un menú tipo, que es representativo de los menús y facilita la planeación, a ese nivel de agregación. Dentro del modelo, la magnitud del periodo de tiempo empleado es igual al tiempo promedio de consumo (TC) de un almuerzo y se supone que los utensilios que se usan vuelven a estar disponibles en el sistema en tres periodos.

Modelo propuesto para medición de capacidad

Índices:

t, periodos de tiempo, donde t (1,2,3,...,s); c, componentes del menú, donde c (1,2,3,...,o); r, recursos (máquinas), donde r (1,2,3,...,k); m, para materia prima, donde m (1,2,3,...,j); q, tiempo en que inicia servicio; lt, Lead time.

Parámetros:

Variables:

S_t, cantidad de almuerzos a servir; X_t, cantidad de almuerzos a producir; Pt, penalización por incumplir demanda, para cada periodo de tiempo ''t''.

Modelo matemático:

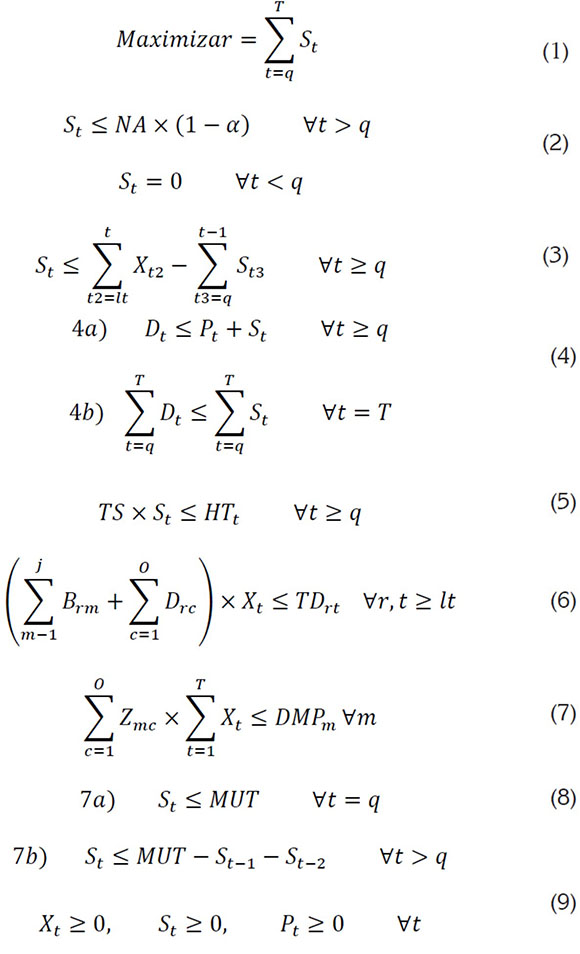
La función objetivo (1) busca garantizar que se sirva la máxima cantidad de almuerzos, de acuerdo con los recursos disponibles; en cuanto a restricciones, se tiene a (2), que asegura que en cada periodo t, la cantidad de almuerzos a servir no supere la cantidad NA de asientos del restaurante; (3) establecer para cada momento que la cantidad de almuerzos a servir no supere la cantidad de almuerzos disponibles para dicho periodo; 4a) garantizar para cada momento la satisfacción de la demanda y 4b) asegura que al final de la jornada, en el periodo , la totalidad de la demanda deberá haber sido satisfecha en su totalidad; (5) evita que en cada periodo t, el tiempo de servir de los almuerzos del periodo supere la duración del periodo; (6) garantiza para cada recurso en cada momento que el tiempo de consumo del recurso no supere el tiempo disponible del recurso; (7) asegura que para cada materia prima , la producción de almuerzos no exceda la disponibilidad de , o sea ; (8) asegura que en cada periodo la cantidad de almuerzo a servir no desborde la cantidad de utensilios disponibles para dicho periodo y (9) restricción de no negatividad.

Validación y caso estudio:

Como caso de estudio, se empleó un restaurante que ofrece un servicio de alimentación a una comunidad universitaria, que sirve en promedio 4.500 almuerzos diarios, lo que lo muestra como uno de los restaurantes con mayor producción diaria del país.

Menús tipo: Dos de los cinco menús -tipo generados- son Clúster 1: crema de zapallo, arroz blanco, bistec, arepa, ensalada de repollo y zanahoria y jugo de guayaba y el Clúster 2: fríjoles, arroz blanco, carne molida con guiso, arepa, en salada de repollo y zanahoria y jugo de lulo.

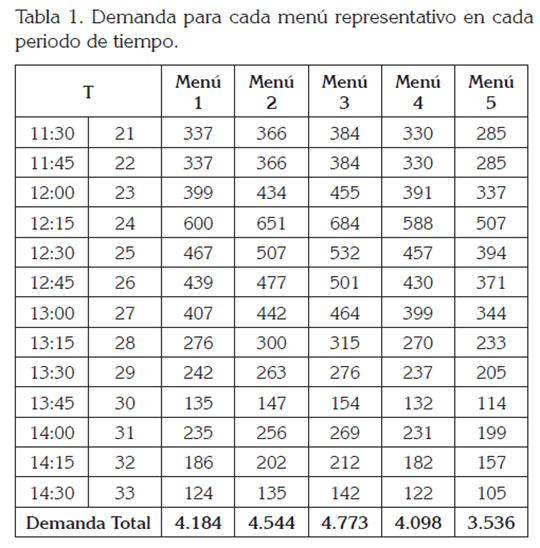
Demanda (Dt): En el análisis de los datos de demanda obtenidos de mediciones del restaurante, se observó que es estable para martes y miércoles, mientras que para lunes, jueves y viernes, la demanda presenta tendencia decreciente. En cada día, la mayor concentración de la demanda se presenta en un intervalo de tiempo de 90 minutos, entre las 12:00 m. y las 1:30 p.m.

Se calculó el porcentaje de participación de la demanda de cada periodo en el día, As. Con esta información, se calculan las demandas en periodos de tiempo de los menús representativos; Dit, el valor de la demanda en cada periodo de tiempo, se calculó con la Ecuación (10). Esta información se observa en la tabla 1.

Tiempo disponible del recurso r (TDrt): Está dado como la duración del periodo de tiempo ''t'', HTt multiplicado por la cantidad de recurso disponible r en ese periodo de tiempo (CR_r), (11).

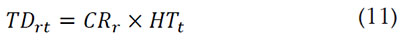
Cálculo de tiempo para servir un almuerzo (TS): La barra de atención esta ordenada como un sistema en serie, por lo tanto, está dado por el tiempo de ciclo en la barra (TS), ecuación (12).

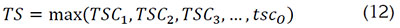
Tiempo de consumo de un almuerzo (TC): El tiempo de consumo de los almuerzos del restaurante universitario, se determinó haciendo 127 mediciones, durante 2 días, del tiempo de consumo de un almuerzo, en cada uno de los comedores, para posteriormente, calcular el promedio de los tiempos de consumo de un almuerzo, determinado en 14,59 minutos, empleado la ecuación (13), donde (CAg) es el consumo de un almuerzo para una determinada cantidad de usuarios y (TU), el total de usuarios.

Tiempo de consumo de recurso r para procesar una porción de materia prima m (Brm): Se determina con la ecuación (14), donde el tiempo de proceso para n porciones de la materia prima es (TPrm); el total de porciones procesadas, de acuerdo a la capacidad del recurso es n y la participación de las materias primas en la mezcla es (Pm).

Cuando se procesa de manera individual la materia prima en un recurso r, la participación (Pm) es 100%; cuando las materias primas son procesadas en conjunto, es decir, se realiza una mezcla w (la vinagreta de la ensalada), se calcula la participación de materias primas en dicha mezcla (Pm), que es el cociente entre la cantidad de materia prima (CMm) y el total de consumo de materias primas que se procesan en la mezcla (CMw), ecuación (15)

Tiempo de consumo de recurso r para procesar una porción de componente c (Drc): Es el cociente entre el tiempo de proceso para n porciones del componente (TPc) sobre el total de porciones procesadas n. ecuación (16).

Cantidad de materia prima consumida para elaborar una porción de componente (Zmc): Se calculan las cantidades de consumo para cada porción, mediante ecuación (17).

Disponibilidad de materia prima m (DMPm): Estos valores fueron proporcionados por la Jefe de programación y planeación de la cafetería

RESULTADOS Y DISCUSIÓN

Al resolver el modelo con los datos recopilados del restaurante universitario, utilizando el software Lingo, se obtuvieron para el menú 2 y el menú 3, los resultados para las variables mostrados en la tabla 2, con un valor en la función objetivo de 4.680 almuerzos, servidos en ambos menús.

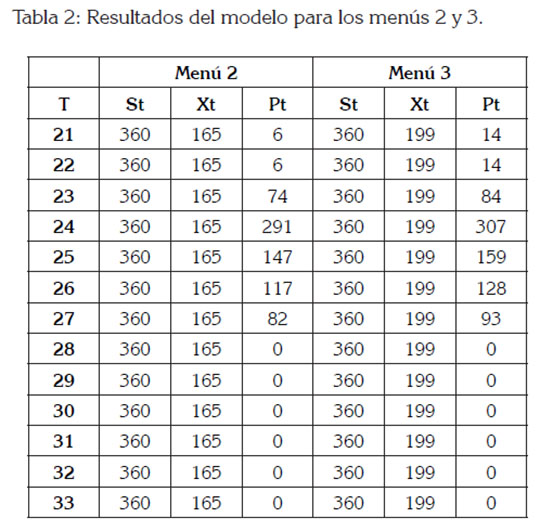
En la figura 2, se observan los resultados del modelo para el menú 2, que contemplan los almuerzos servidos, la demanda, los almuerzos producidos, la penalización y el stock, para ambos menús. Debido a que la producción y el servicio funcionan en distintos periodos de tiempo, se empieza a generar un stock y en el momento en que inicia el servicio, el stock empieza a disminuir.

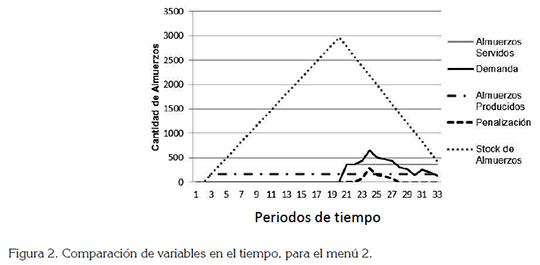
Para evaluar los resultados iniciales del modelo, se realizó un análisis de sensibilidad y se varían algunos parámetros determinantes dentro del ambiente mixto del restaurante universitario, que afecta su capacidad de producción y de servicio. Este análisis, se efectuó para cada menú represen- tativo, pero se muestran solo los resultados del menú 2, debido a que es el más restringido de los cinco trabajados, es decir, que el restaurante se encuentra con menos capacidad de servicio, en este tipo de menú.

Variación del tiempo de consumo (TC): Para el análisis de sensibilidad, se realizó una variación del (TC), desde 12 minutos, con un incremento unitario, hasta 30 minutos. El modelo arrojó solución única, hasta que (TC) tomó el valor de 24 minutos; de 25 minutos en adelante, no se podía satisfacer las restricciones, puesto que la disponibilidad de utensilios no era suficiente para satisfacer la demanda del menú.

El total de almuerzos a servir para un (TC) que varía desde los 12 minutos hasta 23 minutos, siempre toma el valor de 4.680 almuerzos (acumulado). Para un (TC) equivalente a 24 minutos, el valor total de los almuerzos servidos (St) es 4.560 almuerzos y se debe a que, en la situación actual, el parámetro más restrictivo es el servicio en la barra; sin embargo, para cuando el tiempo de consumo es 24 minutos, la disponibilidad de utensilios disminuye tanto, que este factor se vuelve más restrictivo que la disponibilidad del servicio en la barra.

Variación de la demanda: Para este análisis, se evaluó el comportamiento de las penalizaciones (Pt) para variaciones positivas y negativas de la demanda (Dt), del 10 y 20%. En este caso, un incremento de la demanda del 10% hace que el modelo no obtenga solución; este es un resultado esperado, porque la cantidad máxima de almuerzos a servir es 4.680, ajustándose por el tiempo de atención en la barra de servicio y para este menú, un incremento de la demanda esperada, equivale a 5.000 almuerzos, excediendo el valor máximo que el restaurante puede servir de este menú.

Como las penalizaciones son directamente proporcionales a la demanda, al realizar la variación negativa de (Dt), se obtuvieron valores análogos para (Pt). En el periodo de tiempo 24 (12:15 p.m.) es donde las penalizaciones alcanzan su mayor valor, debido a que la demanda aumenta de una manera significativa; luego, la cantidad de penalizaciones se reduce gradualmente.

Variación del tiempo de servir almuerzos (TS): El tiempo empleado en servir un almuerzo se convierte en el factor restrictivo, porque depende, además, del flujo de usuarios, de la disponibilidad de utensilios y de los componentes en la barra de servicio, lo que limita los almuerzos servidos, a 4.680, por cada menú.

Para evaluar la influencia directa de este tiempo en la capacidad de servicio, se establecieron distintos tiempos de servir, para analizar el comportamiento de los almuerzos, en los periodos de tiempo. Los resultados muestran que una disminución en un 20% del tiempo de servir un almuerzo, para el menú 2, puede aumentar la capacidad de servicio, en un 9,17%. Para los distintos tiempos, el comportamiento de los almuerzos servidos depende, inicialmente, del tiempo empleado para servir. Para los tiempos de 5 y 6 segundos, el restaurante no se ve limitado por servicio, así que sirve todos los almuerzos que le permite su capacidad, pero a medida que el tiempo pasa, empieza a verse limitado, por la disponibilidad de bandejas, que es el utensilio más escaso.

En el primer periodo de tiempo, se tiene una disponibilidad en el 100% de las bandejas, es decir, 2.800. Después del primer periodo de tiempo, el uso de las bandejas crea la necesidad de limpieza de las mismas que, de acuerdo al tiempo promedio de consumo de un almuerzo, el factor de disponibilidad de recursos y la capacidad de la máquina, limitan la disponibilidad de bandejas a 560, por periodo de tiempo. El factor de disponibilidad depende de muchos factores, como el consumo en grupo o el descanso después del almuerzo, que reducen la disponibilidad de asientos y de utensilios; en este caso, el factor de reducción utilizado es del 20%, es decir, hay una disponibilidad del 80% de asientos y de bandejas, en cada periodo de tiempo. De este modo, la capacidad de servicio del restaurante es de 7.600 almuerzos.

Del presente estudio, se puede concluir que la capacidad de producción del restaurante es una capacidad variable, no fija. De ningún modo está determinada por la cantidad máxima de almuerzos que se han servido de un menú en un día laboral cualquiera, pues esta información proporciona una idea de la demanda máxima, más no de la capacidad instalada. Con respecto a la capacidad de producción de almuerzos del restaurante es necesario entender que está asociada al menú, a sus tiempos de preparación, a los recursos que utiliza, a la fuerza laboral disponible y al día programado.

Los distintos tiempos de proceso de los componentes de un menú afectan directamente el nivel de servicio, puesto que genera un desbalanceo en el área de producción al no estar listas al mismo tiempo y se puede evidenciar en las distintas barras de servicio, cuando se acaban las porciones de algún componente específico, lo que genera un aumento en el tiempo de servir (TS), retrasando el flujo normal de usuarios.

El modelo de programación lineal propuesto demostró ser una herramienta muy útil, para el análisis de capacidad en ambientes de producción, como el restaurante universitario, por que combina, exitosamente, las características de los ambientes, tanto de servicio como de producción y permite realizar una valoración de los factores críticos, para facilitar la toma de decisiones.

Aunque el modelo permite hacer variaciones de los factores productivos y ver el cambio en el nivel de servicio es muy importante que la información recolectada y suministrada sea confiable, puesto que si no representa la realidad del sistema, los resultados del modelo tampoco lo serán y se puede incurrir en encontrar valores óptimos falsos; esto es importante, porque la mayoría de los tiempos del restaurante están asociados a la noción de temporalidad de los operarios y a la experiencia de trabajo, lo que no es precisamente un reflejo de la realidad y que obligó a hacer mediciones en tiempos de preparación de los componentes de los almuerzos, para tener tiempos de producción más confiables.

Conflicto de intereses: El manuscrito fue preparado y revisado con la participación de todos los autores, quienes declaramos que no existe conflicto de intereses que ponga en riesgo la validez de los resultados presentado.

BIBLIOGRAFÍA

1. AKCALI, E.; MURRAY, J.C.; CHIN, L. 2006. A network flow approach to optimizing hospital bed capacity decisions. Health Care Manage Sci. 9(4):394-404.

2. COROMINAS, A.; OLIVELLA, J.; PASTOR, R. 2010. Capacity planning with working time accounts in services. J. Operat. Res. Soc. 61(2):321-331.

3. DOMÍNGUEZ, J.A.; ÁLVAREZ, M.J.; DOMÍNGUEZ, M.A.; GARCÍA, S.; RUIZ, A. 1995. Dirección de Operaciones: Aspectos Tácticos y Operativos. Ed. McGraw Hill.España. p.215-241.

4. HECHING, A.R.; SQUILLANTE, M.S. 2014. Optimal capacity management and planning in services delivery centers. Performance Eval. 80:63-81.

5. HO, J.W.; FANG, C.C. 2013. Production capacity planning for multiple products under uncertain demand conditions. Int. J. Production Economics. 141:593-604.

6. HUNG, Y.; HUANG, C.; YEH, Y. 2013. Real-time capacity requirement planning for make-to-order manufacturing with variable time-window orders. Computers & Industr. Engin. 64:641-652.

7. HWANG, J.; GAO, L.; JANG, W. 2010. Joint demand and capacity management in a restaurant system. Eur. J. Operat. Res. 207(1):465-472.

8. KALENATIC, D. 2001. Modelo Integral y Dinámico para el Análisis, Planeación, Programación y Control de las Capacidades Productivas en Empresas Manufactureras. Bogotá, Colombia. Universidad Distrital Francisco José de Caldas, Centro de Investigaciones y Desarrollo Científico. p.57-66.

9. KUMRU, M. 2011. Determining the capacity and its level of utilization in make-to-order manufacturing: A simple deterministic model for single-machine multipleproduct case. J. Manufact. Syst. 30:63-69.

10. KURZ, J. 2016. Capacity planning for a maintenance service provider with advanced information. Eur. J. Operat. Res. 251(2):466-477

11. LAGEMANN, H.; MEIER, H. 2014. Robust capacity planning for the delivery of industrial product-service systems. Procedia CIRP. 19:99-104.

12. MANYOMA, P.C.; OREJUELA, J.P.; GIL, C.A. 2011. Metodología para determinar la capacidad instalada en un programa académico. Estudios Gerenciales. 27(121):143-158.

13. MARTÍNEZ, C.; MACHUCA, M.; BENEDITO, E.; COROMINAS, A. 2014. A review of mathematical programming models for strategic capacity planning in manufacturing. Int. J. Production Econ. 153:66-85.

14. PENGFEI, Y.; SANTHOSH, K.G.; JOMON, A.P.; LI, L. 2010. Hospital capacity planning for disaster emergency management. Socio-Econom. Plann. Sci. 44(3):151-160.

15. PEÑA, D. 2003. Análisis de Datos Multivariantes.Ed. McGraw Hill. España. p.227-253.

16. VLACHOS, D.; GEORGIADIS, P.; IAKOVOU, E. 2007. A system dynamics model for dynamic capacity planning of remanufacturing in closed-loop supply chains. Computers & Operations Res. 34:367-394.

17. WOLLMANN, T.E.; BERRY, W.; CLAY WHYBARK, D. 1995. Sistemas de planificación y control de la Fabricación. IRWIN (Madrid). p.143-148.

18. WUTTIPORNPUN, T.; YENRADEE, P. 2007. A new Approach for a Finite Capacity Material Requirement Planning System. Thammasat Int. J. Sci. Technol. 12(2):28-51.

Recibido: Febrero 4 de 2015 Aceptado: Marzo 7 de 2016