
CIENCIAS EXACTAS Y NATURALES-Artículo Científico
SISTEMA DE MONITOREO Y CONTROL PARA UN ROBOT AUTOBALANCEADO SOBRE DOS RUEDAS MODELADO EN 3D
MONITORING AND CONTROL SYSTEM FOR A TWOWHEELED SELF-BALANCING ROBOT MODELED IN 3D
Álvaro Romero1, Alejandro Marín2, Jovani A. Jiménez3
1 Ingeniería de Control, Universidad Nacional de Colombia, e-mail: alromeroac@unal.edu.co
2 Ingeniería de Control, Universidad Nacional de Colombia, e-mail: amarincan@unal.edu.co
3 Doctor en ingeniería, Universidad Nacional de Colombia, Carrera 80 No. 65 - 223, oficina M8A-309, Medellín, (Colombia). Autor para Correspondencia: jajimen1@unal.edu.co
Rev. U.D.C.A Act. & Div. Cient. 17(2): 541-551, Julio-Diciembre, 2014
RESUMEN
El diseño y el control de robot autobalanceado sobre dos ruedas es constituido como un importante avance tecnológico para la movilidad de transporte urbano del futuro, por lo tanto, es una alternativa viable de solución al sistema de transporte inteligente (ITS). Este robot es considerado, en particular, como un problema de excelente referencia para los estudios de control, debido a la tarea compleja de mantener en equilibrio su estructura, por consiguiente, se elabora un sistema realimentado de monitoreo y de control en tiempo real, basado en una red inalámbrica, para sintonizar su punto de equilibrio y verificar el funcionamiento del sistema, por medio de la integración del protocolo ZigBee (estándar IEEE 802.15.4), con el entorno gráfico de programación LabVIEW, con un modelado 3D, que permite visualizar la dinámica del movimiento en el robot. En este artículo, se presenta un prototipo del robot autobalanceado, con la característica de ser un vehículo remoto, para la gestión de movilidad en espacios reducidos.
Palabras clave: Vehículo remoto, robot móvil, diseño de control, red de sensores inalámbricos, modelamiento matemático.
SUMMARY
The design and control of a two-wheeled self-balancing robot, is constituted as an important technological breakthrough for urban transportation and mobility in the future, therefore it is a viable alternative solution to the intelligent transportation system (ITS). This particular robot is considered as an excellent benchmark problem for control studies, because of the complex task of balancing its structure, hence it is developed a feedback system to monitor and control in real time, based on a wireless network to tune a balancing point and verify the operation of the system, through the integration of the ZigBee protocol (IEEE 802.15.4) with the LabVIEW graphical programming environment, furthermore it has a 3D modeling to visualize the dynamics of the robot movement, thus provides a self-balancing robot prototype, with the characteristics of a remote vehicle for mobility management in limited space.
Key words: Remote Vehicles, mobile robot, control design, wireless sensor networks, mathematical modeling.
INTRODUCCIÓN
El rápido crecimiento en la cantidad de automóviles y el pequeño aumento de la infraestructura vial en las grandes ciudades son circunstancias necesarias para la búsqueda de nuevas soluciones en el sistema de transporte, por lo tanto, se están dedicando más esfuerzos en la investigación y el desarrollo de sistemas de transporte inteligente (ITS), por sus siglas en idioma en inglés, con el fin de llegar a una aplicación de transporte autónomo en espacios reducidos e integrado al sistema de control y de monitoreo. Debido a esta problemática, los ITS presentan una importante oportunidad de innovación, que benefician los modelos actuales de transporte, de acuerdo a la integración de nuevas tecnologías de información a los sistemas de transporte que, además, vincula los sistemas de control y de automatización.
El propósito de presentar una alternativa de solución basada en un vehículo autónomo, que contenga las características más influyentes que faciliten la integración al ITS, implica la interconectividad entre el vehículo y la central de monitoreo, la comunicación entre vehículos, el manejo de la información en tiempo real, el registro de las variables y las condiciones del vehículo que presenta frente a la infraestructura vial y, además, pueda atender una eventualidad de modo remoto. De esta manera, introducir nuevos vehículos que brinden las ventajas de los ITS, proporciona un manejo inteligente de la información y estado actual, tanto en las condiciones del vehículo autónomo como en los datos importantes de la movilidad.
El sistema de transporte inteligente es un fenómeno global, que atrae el interés de la industria automotriz y las entidades encargadas del transporte terrestre, que integra un gran número de áreas de investigación (Figueiredo et al. 2001). Cada vez más, aumentan las preocupaciones y los esfuerzos, que se centran en las propuestas de crear un transporte eficaz, eficiente y amigable con el medio ambiente; por lo tanto, los sistemas de transporte inteligente, se convierten en la primera opción (Li & Tang, 2009).
En consecuencia, nacen las propuestas de vehículos y de prototipos para el transporte terrestre, con ventajas y desventajas frente al automóvil tradicional de cuatro ruedas, tales como: el vehículo omnidireccional, que tiene una alta flexibilidad y un alto rendimiento al movimiento, pero presenta una complicada estructura, debido a que muchos rodillos libres están dispuestos en la circunferencia de la rueda y, el vehículo de seis ruedas, con suspensión activa, mejora la movilidad en terrenos difíciles, su principal desventaja consiste en el complejo diseño mecánico, debido al mayor número de ruedas a utilizar, haciendo uso de un mayor recurso de elementos físico-mecánicos para su construcción (Tadakuma et al. 2007; Waldron & Abdallah, 2007).
El vehículo robótico autobalanceado sobre dos ruedas tiene una mejor maniobrabilidad y ocupa menos espacio; además, presenta una estructura mecánica más simple, compacta y con mayor precisión referente al centro de masa, el cual, surge como una alternativa de solución, para el sistema inteligente de transporte (Ishida & Miyamoto, 2010; Waldron et al. 2008; Wook & Jung, 2011). Su mayor limitación radica en mantener el equilibrio, reflejado en un complejo sistema de control (Bin et al. 2010). El robot autobalanceado presenta un complejo sistema de estabilidad, debido a que tiene sólo dos ruedas, como punto de apoyo, y esto lo diferencia del robot diferencial, que utiliza tres ruedas; dos de ellas, controladas individualmente y, otra, como punto de apoyo, mediante una rueda libre (rueda loca), que implica una diferencia importante en el modelo matemático de estos dos robot, que se refleja, a su vez, en el sistema de control (Becker et al. 2012).
Además, el robot autobalanceado sobre dos ruedas (Figura 1) es un vehículo potente y altamente maniobrable sobre un espacio reducido, basado en el principio del péndulo invertido, por el cual, alcanza una estabilización dinámica avanzada, que permite mantener un punto de equilibrio, incluso, mientras lleva una carga pesada (Acosta, 2010). El tamaño, la fiabilidad y las características móviles de estos vehículos y prototipos, se han convertido en una opción importante de abordar entre los investigadores de robots móviles, que se utilizan para estudiar temas, como la planificación de trayectorias y movimientos, con el fin de evadir obstáculos, mediante aplicaciones de inteligencia artificial e integración al sistema inteligente de transporte (Segway Inc., 2009).

En este trabajo, se presenta el diseño e implementación de un robot autobalanceado sobre dos ruedas, integrando un sistema de control y de monitoreo, que propicia la movilidad, de forma autónoma y remota, con seguimiento de la dinámica del robot, en un modelo 3D, visualizado en tiempo real; de esta manera, se aporta un prototipo de vehículo inteligente, para el sistema de transporte en el siglo XXI.
En el artículo, se describe el modelo matemático del robot autobalanceado y las consideraciones a tomar sobre la integración del sistema de control y el monitoreo remoto. Los resultados registrados en el sistema de monitoreo se analizan, ante el efecto de las perturbaciones, sobre las señales de control y el ángulo de inclinación, contrastadas con el comportamiento dinámico del robot en equilibrio. Con el objetivo de registrar las condiciones reales, intervienen en el correcto funcionamiento del robot, que permita identificar los puntos críticos del sistema controlado.
MATERIALES Y MÉTODOS
El prototipo del robot autobalanceado sobre dos ruedas presenta una alternativa de movilidad inteligente, de esta manera, se describe el modelado matemático, el control en lazo cerrado, la integración de monitoreo, mediante el entorno de programación en LabVIEW y las comunicaciones inalámbricas, basada en el protocolo ZigBee.
El éxito del robot autobalanceado, se debe, inicialmente, a la inspiración del vehículo SEGWAY®, creado en el 2001, por Dean Kamen y que es la principal alternativa comercial en vehículos unipersonales; además, este tipo de transporte, busca una solución para la descongestión en los centros de las grandes ciudades, donde la gente utiliza un automóvil para realizar recorridos cortos. De esta manera, estos dispositivos de movilidad, buscan reemplazar al automóvil convencional en tareas rutinarias, que no requieren mayor capacidad y, a su vez, permiten movilidad entre los peatones sin molestarlos. Es muy importante considerar que la disposición de sus ruedas permite un giro sobre el mismo eje, otorgando así una maniobrabilidad única respecto de otros tipos de vehículos (Moreno & Duarte, 2009).
Para llevar a cabo el éxito de este dispositivo de movilidad en el transporte urbano, se debe tener en cuenta que su puesta en marcha depende de la cooperación de los sectores público y privado, especialmente, en las áreas de seguridad, el uso de las vías, las políticas y legislación, la aceptación de los usuarios y los enfoques de mercado (Miller et al. 2010).
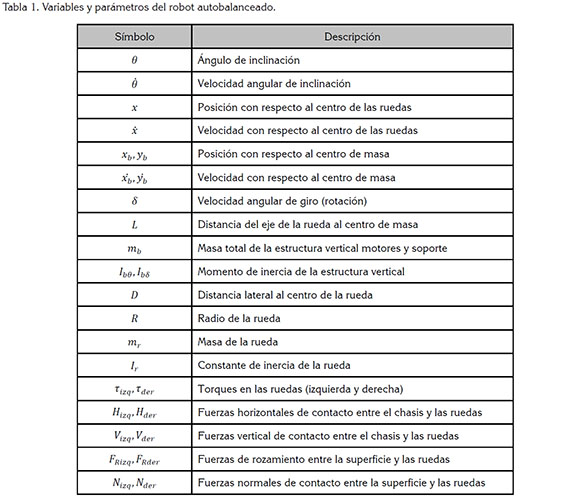
El modelo matemático del robot autobalanceado, se ilustra en un esquema general, mediante la figura 2, en la cual, se describe el modelo simplificado del robot autobalanceado sobre dos ruedas, visto desde tres perspectivas, por lo tanto, se considera: la vista lateral, para determinar el ángulo de inclinación que presenta la estructura (Figura 2a); las dinámicas de torque y fuerzas ejercidas sobre las ruedas (Figura 2b) y, en vista frontal, la distancia entre el centro del robot y el eje de la rueda (Figura 2c). Posteriormente, se relacionan las variables y los parámetros del modelo en la tabla 1 (Jun & Minglun, 2010).
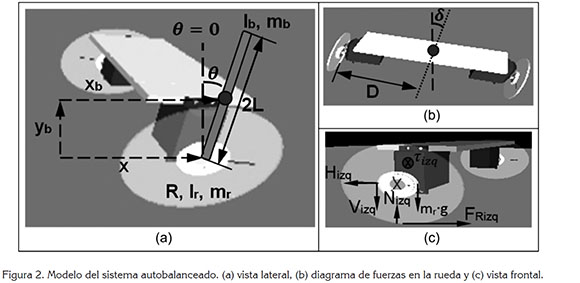
El sistema del robot autobalanceado (Figura 2a), se modela, inicialmente, mediante la extracción del diagrama de cuerpo libre de la rueda (Figura 2b), de esta manera, se considera un trato similar de la rueda izquierda y derecha; además, se debe tener en cuenta, para este análisis, que la rueda no resbala sobre la superficie (Igarashi et al. 2008; Majewski, 2013).
En la ecuación 1, se relacionan las fuerzas horizontales de contacto entre el chasis y las ruedas (Hizq, Hder); de igual manera, para la fuerza vertical (Vizq, Vder), las fuerzas de rozamiento entre la superficie y las ruedas (FRizq, FRder) y, por último, las fuerzas normales de contacto entre la superficie y las ruedas (Nizq, Nder).
A partir del análisis de los diagramas de cuerpo libre de la figura 2, se obtienen las ecuaciones correspondientes de las ruedas del lado izquierdo: Ecuaciones 1, 2, y 3) y derecha: Ecuaciones 4, 5 y 6:
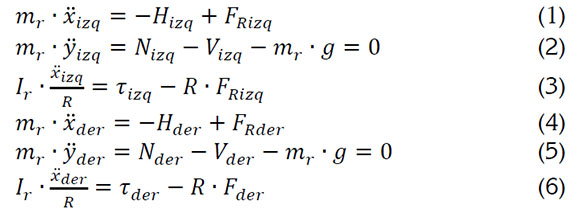
Una consideración importante, radica que la referencia del sistema es fija en el centro del robot autobalanceado, por lo tanto, la posición respecto a las ruedas: xizq=xder=x, yizq=yder=y. De esta manera, se tienen las ecuaciones 7 y 8:
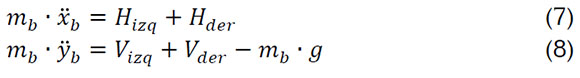
Las ecuaciones 9 y 10 representan el momento angular involucrado en la inclinación y giro del vehículo:
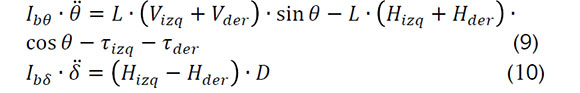
Por consiguiente, es necesario considerar la relación de la posición del centro de masa (x, y) y el centro de masa del chasis (xb, yb), para describir las ecuaciones 11, 12, 13, 14, 15 y 16:
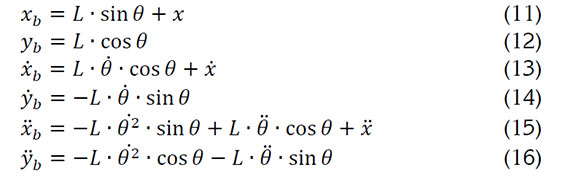
Luego, de tomar las consideraciones de las ecuaciones 11- 16, en las ecuaciones 7-10, se obtiene las ecuaciones 17, 18, 19 y 20:
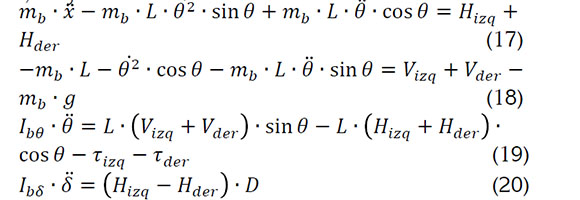
Por medio de las ecuaciones relacionadas en el análisis anterior, se llega a las ecuaciones dinámicas del sistema, que representan el modelo del robot autobalanceado, como los describen las siguientes tres ecuaciones diferenciales: Ecuaciones 21-23:
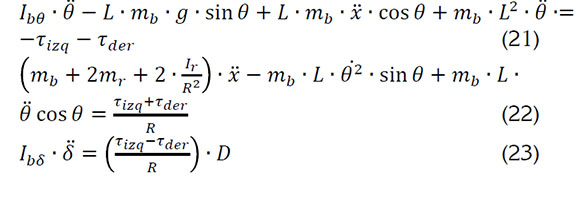
Posteriormente, el sistema de ecuaciones se linealiza en el punto de equilibrio, es decir, cuando el robot autobalanceado se encuentra en cero grados del ángulo de inclinación (θ=O), de esta manera, se tienen las ecuaciones 24, 25 y 26:
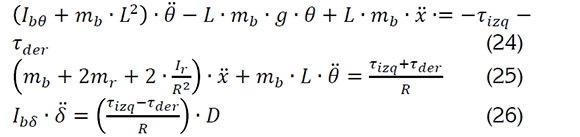
Con las ecuaciones 25-26, se obtienen las ecuaciones 27, 28 y 29, en las cuales, se representan los valores constantes (a, b, c, d y e), en las respectivas ecuaciones 30, 31, 32, 33 y 34:
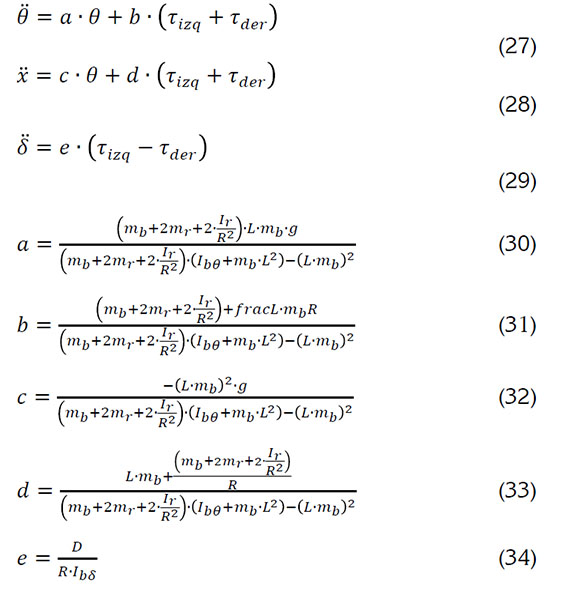
Luego de conocer el modelo matemático del sistema, se continúa con el análisis en el sistema de control y de monitoreo; para tal propósito, se presenta el sistema de control y el sistema de monitoreo remoto.
Diseño del sistema control y monitoreo: El sistema está compuesto por dos etapas: la parte de control, se encarga de mantener el equilibrio del robot (sistema de control) y, la parte de monitoreo, supervisa el funcionamiento del sistema y puede ver la dinámica del robot en tiempo real, en modelado 3D (sistema de monitoreo remoto), además, puede tomar decisiones de ajuste en el ángulo de inclinación.
Sistema de control: El sistema de control está conformado por: la planta que representa el robot autobalanceado sobre dos ruedas; el acelerómetro, como el sensor encargado de la toma de datos del ángulo de inclinación; el controlador, compuesto por un microcontrolador (PIC16F887), que cumple la función de calcular el ángulo de error y ajuste, para mantener el robot en equilibrio, a través de una señal de modulación por ancho de pulso PWM (Pulse-Width Modulation), que actúa por medio de una etapa de potencia, para suministrar la energía y el sentido de giro necesario para cada motor acoplado a las ruedas del robot, en la posición de equilibrio (Servín & Saldoval, 2012).
Además, se debe considerar que el sistema de control del robot autobalanceado es una representación extendida del péndulo invertido, de esta manera, se puede analizar el sistema de control, mediante el comportamiento del péndulo invertido; no obstante, en (Romero et al. 2013), el diseño de controladores Realimentación Lineal en Variables de Estado (RLVE) y Regulador Cuadrático Lineal LQR, para el péndulo rotacional invertido (ROTPEN), considera que el sistema es inestable y, de acuerdo con ello, se linealiza en el punto de operación en equilibrio, es decir, cuando el péndulo invertido está en posición vertical hacia arriba, lo cual, es similar cuando un objeto o persona está sobre el robot autobalanceado, de esta manera, se considera que el sistema en controlable, por lo tanto, se debe regir los parámetros de operación en el punto de equilibrio, para lograr establecer una acción de control adecuada y permitir que el robot autobalanceado se mantenga estable.
De acuerdo a las consideraciones anteriores, se implementó un controlador proporcional en lazo cerrado, cuyos parámetros se determinaron empíricamente, mediante distintas pruebas preliminares, realizadas sobre el robot, teniendo en cuenta tres aspecto importantes: la señal de control, generada mediante el ciclo de dureza del PWM; la señal de salida del sistema, medida sobre ángulo de posición del robot y, el punto de equilibrio del robot; sin embargo, se realizaron algunas variaciones al controlador clásico (Figura 3), en el cual, se monitorea de forma remota: la señal de control y la señal de salida del sistema, con el propósito de registrar las condiciones dinámicas del robot autobalanceado, que permitan reconstruir en tiempo real, un modelo 3D; además, se consideran perturbaciones en la planta respecto al peso y a la posición del robot.
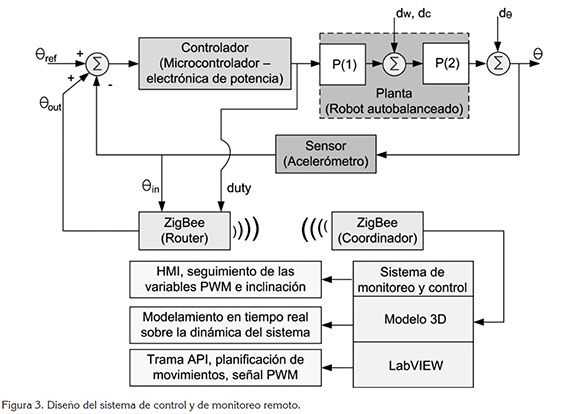
En la figura 3, se tiene el diseño del sistema de control y de monitoreo remoto, representado en diagrama de bloques y se observa un lazo de control realimentado, que toma como referencia el ángulo de inclinación (θref), dado que el objetivo del robot es mantenerse en equilibrio ante perturbaciones, tales como: el cambio de masa del sistema al agregar peso en el chasis robot (dω); el cambio del centro de masa, cuando se adiciona el mismo peso en el chasis, pero ubicado en los extremos del robot (dc) y, el cambio en el ángulo de equilibrio, al aplicar una fuerza contraria al movimiento del robot (dθ).
Dado que las perturbaciones (dω, dc) solamente difieren en la ubicación del peso en el chasis, que pueden ir en el mismo punto, considerando que se aplica una sola perturbación a la vez; además, son perturbaciones que afectan directamente los parámetros de la planta y alteran también, de manera directa, el modelo matemático. En consecuencia, el sistema de control representado en diagrama de bloques, toma la planta como la representación de dos subsistemas (P(1), P(2)) y, entre ellos, se aplican las perturbaciones (dω, dc), (Goodwin et al. 2001).
Sistema de monitoreo remoto: El sistema de monitoreo complementa el esquema presentado en la figura 3, que consiste, principalmente, en la comunicación inalámbrica, basada en el protocolo ZigBee, estándar de comunicación inalámbrica IEEE 802.15.4, que utiliza radiodifusión digital, para el envío de datos, el cual, transmite desde el ZigBee router (nodo enrutador de la red), ubicado en el robot autobalanceado al ZigBee coordinador (nodo administrador de la red), conectado al computador, por lo tanto, se establece el monitoreo remoto, sobre el robot autobalanceado (Chen et al. 2012). De esta manera, se envían las variables medibles del sistema, como: el ángulo de inclinación (θin), y el ciclo de dureza (duty) de la señal PWM (Figura 3).
Posteriormente, estas señales recibidas por el ZigBee coordinador son analizadas por el entorno de programación Lab- VIEW (Figuras 3 y 4), con el propósito de reconstruir las señales sensadas (θ, duty) y, de esta manera, se presenta en la HMI, por sus siglas en idioma inglés (Human Machine Interface), la dinámica del movimiento del robot en un modelado 3D (Cao et al. 2011). Además, este sistema, a su vez, cuenta con la opción de adicionar a la referencia un ángulo de ajuste (θout) de forma remota, en situaciones no deseadas en el robot.

El sistema integrado de monitoreo y de control para el robot autobalanceado sobre dos ruedas está compuesto por: (1) la dinámica del modelo 3D; (2) la señal analógica del ángulo de inclinación (0 a 180) grados; (3) la señal PWM con un ciclo duty (0 a 100)%; (4) indicadores de desplazamiento del robot, según el grado de inclinación (adelante, atrás); (5) Robot autobalanceado sobre dos ruedas; (6) diseño gráfico HMI; (7) dispositivo enrutador de la red inalámbrica ZigBee y, (8) Sistema de control y etapa de potencia (Figura 4).
RESULTADOS Y DISCUSIÓN
Los resultados experimentales registrados bajo el sistema integrado del robot, comunicaciones ZigBee e interface gráfica HMI en LabVIEW, permiten realizar un seguimiento en tiempo real, sobre las variaciones que afectan al robot y que no están relacionadas en el modelo matemático, lo cual, permite ajustar los parámetros de control, que inciden directamente con las perturbaciones, a las que fue sometido el robot.
De esta manera, se presentan los resultados, relacionando las perturbaciones y el ciclo de dureza del PWM, como señal de control, lo que permite obtener una base de datos, para un análisis posterior, que profundice en los factores que afectan la estabilidad del robot. La importancia de presentar esta relación de resultados consiste en brindar mejores herramientas para el diseño de control y, a su vez, se muestre como una alternativa para la construcción de nuevos prototipos, teniendo en cuenta el seguimiento en tiempo real, sobre las condiciones que afectan el buen desempeño del robot. El comportamiento del sistema al adicionar las perturbaciones (dω, dc y dc), se analizan por separado, con el propósito de encontrar la relación y el efecto de cada perturbación, con la señal de control PWM, registrando el ciclo duty, en valor porcentual y el ángulo de inclinación (Tabla 2).
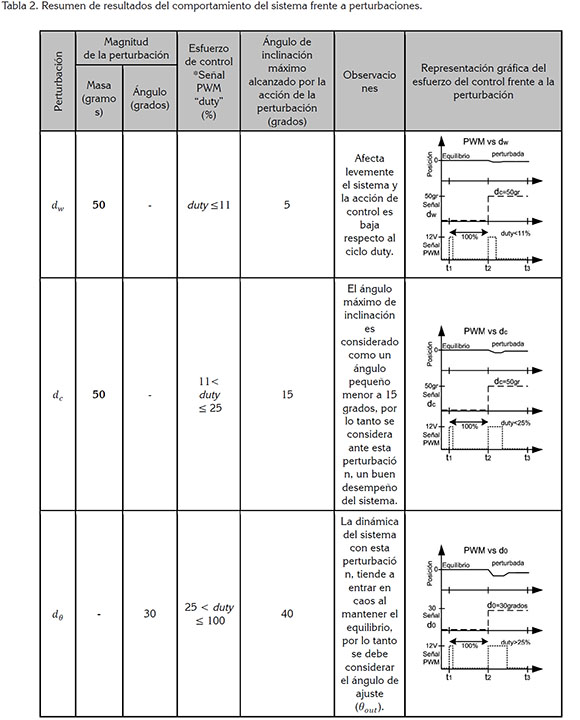
Para este análisis, se toma el resultado de 200 muestras promediadas, que se resumen de la siguiente manera: en primer lugar, la perturbación que adiciona peso al robot en el centro de masa (dω), no presenta un mayor esfuerzo de control y su incremento en el ciclo duty no supera el 11% de la señal; en segundo lugar, la perturbación que adiciona peso en los extremos del robot (dc), presenta un mayor esfuerzo de control y su incremento en el ciclo duty, se encuentra entre 11 y el 25% de la señal y, en tercer lugar, la perturbación que ejerce un cambio en el ángulo de inclinación en el robot (dθ), presenta un esfuerzo de control considerable y su incremento en el ciclo duty, supera el 25% de la señal (Seghour et al. 2011; Lee et al. 2009).
Las perturbaciones (dω, dc y dθ) sobre el sistema, ejercen una acción de control mínima, de acuerdo al ciclo duty, si solamente esta señal de control tiene una respuesta muy rápida y acorde a la dinámica del robot; en caso contrario, la acción de control puede llevar al robot a perder el ángulo de equilibrio y a tornarse inestable, hasta precipitarse al suelo. Estos efectos, se deben, principalmente, a: retardos en el cálculo de la acción de control, ruidos que infieren en la señal sensada y rizados en la señal del suministro de energía a los motores y, a la vez, se deben tener en cuenta las condiciones externas del medio en que interactúa el robot (Lee & Jung, 2012).
Un valor agregado de este sistema de control es que permite adicionar una señal de referencia de ajuste (θout), que proviene del sistema de monitoreo de forma remota, lo cual, es tenido en cuenta por la sumatoria del error, por lo tanto, la señal de error, en este caso, está vinculada con: la señal de referencia (θref), la señal de ajuste (θout) y la señal de la salida realimentada (θin), que permite ajustar la señal de error en situaciones no deseadas en el robot y, de esta manera, se logra mantener en equilibrio; esta implementación fue bien acogida por el sistema y sirve como medida preventiva, cuando el robot tome comportamientos no deseados y atípicos (Chen, 2012).
El prototipo de vehículo autobalanceado busca reemplazar al automóvil convencional en tareas rutinarias, que no requieren mayor capacidad de carga. Además, al ser un vehículo unipersonal (existen vehículos para dos pasajeros), permite que el diseño sea lo suficientemente pequeño para poder transitar entre los peatones sin obstaculizarlos, tanto en vías de acceso peatonal como de automóviles; la disposición de sus ruedas permite un giro sobre el mismo eje del vehículo, otorgando así una maniobrabilidad única, respecto de otros tipos de vehículos (Nguyen et al. 2004).
Como conclusión, se puede decir que por condiciones externas, que no se tienen en cuenta en el modelo matemático del robot autobalanceado, se presentan factores que afectan directamente el buen funcionamiento del robot, como: las corrientes de aire, los cambios de la rugosidad en la superficie, la inclinación del terreno, el desplazamiento de la carga sobre el robot, el cambio en el centro de masa al colocar peso en otro punto diferente del centro de masa, rizados en el suministro de energía y señal PWM, pérdida de datos en el sensor, retardos en la transmisión y recepción de datos por comunicación inalámbrica, entre otros, que pueden llevar al robot a un punto de operación caótico para el sistema de control, el cual, no sea suficiente para mantener el propósito de operar en la posición de equilibrio.
Los sistemas autónomos en los robots que interaccionan con el medio que ocupan los humanos, como las vías de transporte, son aun sistemas que se deben integrar a un sistema de monitoreo y control, de acuerdo a los factores mencionados, que afectan la dinámica y el buen desempeño del robot autobalanceado; se debe garantizar el funcionamiento del sistema y tomar decisiones frente a condiciones no deseadas, de forma remota.
Para trabajos futuros, se sugiere hacer un diseño simultáneo entre el modelo de robot autobalanceado y el sistema de control, con el propósito de dimensionar un esquema de control adecuado, para soportar las condiciones extremas que presente la dinámica del robot, por lo tanto, las dimensiones del diámetro de las ruedas y peso del robot son fundamentales para obtener un mejor desempeño en el equilibrio; además, en la parte de control, se requiere: ajustar la resolución en la medida sobre la inclinación del robot, entre 10 a 12 bit y, adicionar la medición de la velocidad angular y, de esta manera, se lograría obtener datos importantes sobre el sistema, para tomar una acción de control asertiva, frente a la dinámica del robot.
Conflicto de intereses: El manuscrito fue preparado y revisado con la participación de todos los autores, quienes declaramos que no existe ningún conflicto de intereses, que ponga en riesgo la validez de los resultados presentados. Financiación: Este trabajo fue financiado por el Departamento Nacional de Ciencia, Tecnología e Innovación -COLCIENCIAS-, por medio del proyecto de investigación "Sistema sensórico para la inspección de autopartes en la línea de ensamble", aprobado en la convocatoria "569-2012 Banco de Proyectos elegibles de CTeI".
BIBLIOGRAFÍA
1. ACOSTA, J.Á. 2010. Furuta pendulum: a conservative nonlinear model for theory and practise. Disponible desde Internet en http://www.hindawi.com/journals/mpe/2010/742894/ [con acceso el 06/02/2014].
2. BECKER, A.; ONYUKSEL, C.; BRETL, T. 2012. Feedback control of many differential-drive robots with uniform control inputs. Intelligent Robots and Systems (IROS), 2012 IEEE/RSJ International Conference on (Portugal). p.2256-2262.
3. BIN, H.; ZHEN, L.; FENG, L. 2010. The kinematics model of a two-wheeled self-balancing autonomous mobile robot and its simulation. IEEE International Conference on Computer Engineering and Applications (Estados Unidos). 2:65-68.
4. CAO, J.; LIN, L.; LI, Y.; HUO, T.; DAI, F. 2011. The measurement and control system for pipe inspection robot based on LabVIEW. IEEE Artificial Intelligence, Management Science and Electronic Commerce (Estados Unidos). p.4497-4500.
5. CHEN, C.; LIN, H.; HUANG, Y.; CHEN, Y. 2012. Power management system based on ZigBee. IEEE Anti- Counterfeiting, Security and Identification. (Estados Unidos). p.1-5.
6. CHEN, M. 2012. Analysis and design of robust feedback control systems for a nonlinear two-wheel inverted pendulum system. IEEE International Symposium on Computer, Consumer and Control. (Estados Unidos). p.1-5.
7. FIGUEIREDO, L.; JESUS, I.; MACHADO, T.; FERREIRA, J.; DE CARVALHO, J. 2001. Towards the development of intelligent transportation systems. IEEE Intelligent transportation systems. (Estados Unidos). p.1206-1211.
8. GOODWIN, G.; GRAEBE, S.; SALGADO, M. 2001. Control system design. Prentice Hall, (Estados Unidos). p.401-485.
9. GARASHI, H.; SAITO, T.; KINJYO, T.; MATSUNO, F. 2008. Development of an autonomous inverted pendulum mobile robot for outdoor environment. IEEE SICE Annual Conference. (Estados Unidos). p.2282-2285.
10. ISHIDA, S.; MIYAMOTO, H. 2010. Ball wheel drive mechanism for holonomic omnidirectional vehicle. IEEE World automation congress © 2010 TSI Press. (Estados Unidos). p.1-6.
11. JUN, S.; MINGLUN, W. 2010. Modeling and simulation for self-balance system. IEEE International Conference on Digital Manufacturing & Automation. (Estados Unidos). 1:951-955.
12. LEE, H.; JUNG, S. 2012. Balancing and navigation control of a mobile inverted pendulum robot using sensor fusion of low cost sensors (Estados Unidos). Sci. Direct Mechatron. 22(1):95-105.
13. LEE, H.; RYU, S.; LEE, J. 2009. Optimal posture of mobile inverted pendulum using a single gyroscope and tilt sensor. IEEE ICROS-SICE International Joint Conference. (Estados Unidos). p.865-870.
14. LI, L.; TANG, S. 2009. Intelligent transportation systems in China. IEEE, Intelligent Transportation Systems. (Estados Unidos). 1(2):5-40.
15. MAJEWSKI, T. 2013. Vibratory Forces and Synchronization in Physical Systems. (Mexico). Ing. Mec. Tecnol. Desarrollo. 4(4):119-128.
16. MILLER, S.; KENNEDY, J.; MOLINO, J.; EMO, A.; ROUSSEAU, G.; TAN, C.; DO, A. 2010. Operating characteristics of the segway tm human transporter monique. National Technical Information Service (Estados Unidos). p.2-58.
17. MORENO, L.; DUARTE, M. 2009. Diseño e Implementación de Vehículo Autobalanceado sobre Dos Ruedas. Disponible desde Internet en http://www.cec.uchile.cl/~lemoreno/dat/paper_memoria_BORRADOR.pdf [con acceso el 01/06/2014].
18. NGUYEN, H.; MULLENS, K.; BURMEISTER, K.; FARRINGTON, N.; MORRELL, J.; MILES, S.; THOMAS, K.; GAGE, D. 2004. Segway robotic mobility platform. (Estados Unidos). p.207-220.
19. ROMERO, A.; CANO, M.; JIMÉNEZ, J. 2013. Modelado, simulación e implementación de controladores LQR y RLVE al sistema péndulo invertido rotacional usando la plataforma NI ELVIS II. (Colombia). Rev. Cient. Guillermo de Ockham. 11(1):67-78.
20. SEGHOUR, S.; BOUCHOUCHA, M.; OSMANI, H. 2011. From integral backstepping to integral sliding mode attitude stabilization of a quadrotor system real time implementation on an embedded control system based on a dsPIC uC. (Estados Unidos). p.154-161.
21. SEGWAY INC. 2009. Segway advanced development, P.U.M.A. (Personal Urban Mobility & Accessibility). (Estados Unidos). Disponible desde Internet en http://www.segway.com/puma/ [con acceso el 02/06/2014].
22. SERVÍN, G.; SALDOVAL, L. 2012. Prototype for a selfbalanced personal transporter. IEEE Workshop on engineering applications. (Estados Unidos). p.1-6.
23. TADAKUMA, K.; TADAKUMA, R.; BERENGERES, J. 2007. Development of holonomic omnidirectional. Proceedings of the 2007 IEEE/RSJ International conference on intelligent robots and systems. (Estados Unidos). p.35-39.
24. WALDRON, J; ABDALLAH, M. 2007. An optimal traction control scheme for off-road operation of robotic vehicles. IEEE/ASME Transact. On Mechatron. (Estados Unidos). 12(2):126-133.
25. WALDRON, J.; HUNG, T.; MADADNIA, J. 2008. Configuration design of a robotic vehicle for rough terrain mobility. IEEE International conference on mechatronics and machine vision in practice. (Estados Unidos). p.487-492.
26. WOOK, H.; JUNG, S. 2011. Design and analysis of a robotic vehicle balancing mechanism. IEEE International conference on ubiquitous robots and ambient intelligence. (Estados Unidos). p.855-857.
Recibido: Noviembre 2 de 2013 Aceptado: Agosto 29 de 2014

Revista U.D.C.A Actualidad & Divulgación Científica por Universidad de Ciencias Aplicadas y Ambientales se distribuye bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.