CIENCIAS AGROPECUARIAS-Artículo Científico

ESTABILIDAD FENOTÍPICA DE UNA COLECCIÓN DE FRÍJOL ANDINO (Phaseolus vulgaris L.) TIPO ARBUSTIVO

PHENOTYPIC STABILITY OF SHRUB BEAN (Phaseolus vulgaris L.) COLLECTION

Gustavo A. Ligarreto M.¹; Oscar A. Castro H.²; Bernardo Cháves C.³

¹ I.A. Ph.D., Profesor Asociado. Facultad de Ciencias Agrarias. Universidad Nacional de Colombia. Bogotá, e-mail: galigarretom@unal.edu.co

² I.A., Departamento de Nutrición. Instituto Colombiano de Bienestar Familiar, ICBF. Bogotá, e-mail: oscar.castro@icbf.gov.co

³ M.Sc., Department of Biological Systems Engineering and Horticultural Crops Research Unit, USDA. Washington State University. Pullman, WA (USA), e-mail: b.chavescordoba@wsu.edu

Rev. U.D.C.A Act. & Div. Cient. 18(1): 109-118, Enero- Junio, 2015

RESUMEN

El cultivo del fríjol es una actividad agrícola familiar que, generalmente, se produce bajo condiciones de estrés biótico y abiótico, por ello, se necesita seleccionar materiales estables, con buen potencial de rendimiento, para contribuir a la seguridad alimentaria y a la competitividad. La investigación, se realizó para evaluar la estabilidad fenotípica de 13 accesiones de fríjol rojo arbustivo, con crecimiento determinado de una colección de referencia, en cinco ambientes, con clima templado y frío, en Colombia. El análisis de estabilidad fenotípica, se realizó con las metodologías de Eberhart & Russell, Wricke y Shukla y AMMI. Los análisis permitieron determinar que los cultivares ICA Cerinza y Boyacá 18 fueron los más estables, con rendimiento potencial mayor al promedio. Perú 40 y Diacol Andino fueron los de mayor potencial de rendimiento, pero los más inestables, mientras que por el método AMMI, se detectó que todos los ambientes, excepto Mosquera 4, aportaron significativamente a la GxA, alcanzando el 79,07% de la varianza acumulada, en los dos primeros componentes principales.

Palabras clave: Interacción GxA, regresión, ecovalencia, varianza de estabilidad, AMMI.

SUMMARY

The bean crop is a familiar agricultural activity, generally produced under conditions of biotic and abiotic stress. Therefore, it is necessary to select stable materials with good yield potential, to contribute to the food security and competitiveness. The research aimed to evaluate the phenotypic stability of 13 red shrub bean accessions of a reference collection in five environments with moderate and cold climate conditions in Colombia. The stability analysis was realized using Eberhart & Russell, Wricke y Shukla and AMMI methodologies. The analysis of the results showed that ICA Cerinza and Boyacá 18 were the most stable genotypes with higher yield potential than the average. Perú 40 and Diacol Andino genotypes were very high in yield but they were the most unstable ones. The AMMI analysis showed that the environments contributed significantly to the GxE, except for Mosquera 4, with 79.09 % of the variance for the two principal components.

Key words: GxE interaction, regression, ecovalence, stability variance, AMMI.

INTRODUCCIÓN

El fríjol común es uno de los alimentos más importantes en la dieta básica de la población en países de Latinoamérica, gracias a su alto aporte proteínico, que alcanza el 22%, al suministro de carbohidratos y de elementos minerales esenciales (Caldas & Blair, 2009). La especie en los últimos años ha perdido competitividad, entre otros factores, porque la producción de fríjol se obtiene bajo condiciones de ambientales con estrés, tanto biótico como abiótico, lo que redunda en un bajo rendimiento (Arias et al. 2007).

Los estudios de interacción genotipo por ambiente (GxA) en fríjol, específicamente, no son tan abundantes, como los realizados en otras especies, tales como maíz, cebada y trigo (Vizgarra et al. 2012). Cuando se trabaja en forma regional en la evaluación del comportamiento de los genotipos de fríjol, en distintas localidades, a través de los años, se debe reconocer que el entorno ambiental no es homogéneo para el propósito del análisis, por lo mismo se prefiere agrupar los materiales por características genéticas, como hábito de crecimiento y color (Vizgarra et al. 2012).

Antecedentes de la interacción genotipo por ambiente. Para entender la respuesta fenotípica de una variedad en las zonas de producción es necesario descomponer la función productiva en el genotipo (G) y el ambiente (A) (Lynch & Walsh, 1998). Se puede estudiar, claramente, la dependencia o independencia del genotipo a condiciones específicas ambientales, es decir, se analiza la interacción genotipo por ambiente GxA en el comportamiento de la variable en estudio (Vargas et al. 1999).

Yates & Cochran (1938) sugirieron que la GxA se comporta linealmente respecto al efecto ambiental (ga)ij=ξiej+dij, donde ξi, es el coeficiente de regresión lineal y dij es una desviación. Esta aproximación univariada fue ampliada por Finlay & Wilkinson (1963) y luego por Eberhart & Russell (1966), que además del coeficiente de regresión (βj), se enfoca en la medición de la desviación de las observaciones frente a la predicción del modelo (S²di). Para estos autores, un genotipo tiene una expresión estable en experimentos en diferentes ambientes, cuando contribuyen poco sobre la magnitud del GxA, por ello, es necesario identificar cuales de estos genotipos son estables y con alto potencial de rendimiento. Los componentes lineal (βi) y no lineal (S²di) de la GxA son necesarios para evaluar la estabilidad de los genotipos. Wricke (1962) propuso la Ecovalencia (W), que se deriva de la partición de la GxA en sumas de cuadrados que cada genotipo aporta a dicha interacción. Similar al método anterior, Shukla (1972) fraccionó la suma de cuadrados de la GxA dentro de componentes para cada genotipo, separadamente, considerando la varianza de estabilidad σi2 del i-ésimo genotipo. Cuando σi2 es muy grande, los genotipos se consideran inestables (Kang, 2003).

Según Finlay & Wilkinson (1963), la estabilidad es una respuesta o una característica que no cambia su expresión en espacio y tiempo. A nivel genotípico, la estabilidad es el atributo que le permite a un genotipo ajustar la capacidad productiva a la más amplia variación del estímulo ambiental, cuando son evaluados en ambientes diferentes (Ceballos, 1998). Los cambios en el ranking de los genotipos en ambientes, puede ser explicada por las variaciones en sensibilidad inter e intra-especies a ambientes con diferentes condiciones (Ebdon et al. 1998). Un genotipo es estable si su respuesta es paralela al promedio de todos los genotipos e interactúa menos con el ambiente (Eberhart & Russell, 1966).

Gollob (1967), propuso un término bilineal para la GxA (ga) ij= Σⁿ _k=1λn γgn ηan en el cual λ1 ≥ λ2...≥ λn y γgn ηan satisfacen las restricciones Σ γgn γgn' = Σ ηan ηan' = 0 para n ≠n' y Σ γ²gn = Σ η²an = 1. Esta estructura se inserta, generando un modelo lineal-bilineal Ygar= μ + σg + βa + Σⁿ_k=1 λn γgn ηan + θga+εgar, que es una generalización de la regresión, con mayor flexibilidad para la descripción de GxA, pues considera más de una sola dimensión genotípica y ambiental. Este modelo multivariado, se conoce como AMMI, (Zobel et al. 1988; Crossa, 1990; Gauch, 1992; Vargas & Crossa, 2000).

El análisis AMMI considera que los efectos de los genotipos y ambientes son aditivos y lineales, mientras que la GxA tiene efectos multiplicativos, que puede ser expuesta mediante el análisis de componentes principales, para una mejor interpretación. De acuerdo con Ebdon et al. (1998), éste análisis ha mostrado ventajas sobre modelos de efectos fijos al tener mayor efectividad, porque el modelo contiene más de la suma de cuadrados de la GxA.

El modelo AMMI está representado por la siguiente ecuación:

Ygar= µ + σg + βa + Σⁿ_k=1 λn γgn ηan + θga+ εgar

Donde Ygar es el rendimiento observado del genotipo g en el ambiente a y en la repetición r. Los parámetros aditivos son:

El objetivo de esta investigación, consistió en evaluar la estabilidad fenotípica de 13 genotipos de fríjol andino de hábito de crecimiento determinado y grano rojo, a partir del análisis de la interacción genotipo x ambiente, empleando tres métodos estadísticos de diferente sensibilidad.

MATERIALES Y MÉTODOS

Localización. Los ensayos de ambientes múltiples, se realizaron en cuatro semestres consecutivos, en el municipio de Mosquera, Cundinamarca (4° 42' N, 74° 12' W), a 2540 msnm, precipitación por ciclo de cultivo de 396, 242, 267 y 149mm numerados en su orden: Mosquera 1, Mosquera 2, Mosquera 3 y Mosquera 4, respectivamente, con temperatura promedio de 13°C, suelos de pH 5,9, textura franco limosa, 3,7% de materia orgánica; P 30 ppm, 31,8 me CIC/100g de suelo; 19,0me Ca/100g, 2,8me Mg/100g, 0,19me K/100g y 0,63me Na/100g. El ambiente 5, se desarrolló en el municipio Darién, Valle del Cauca, (3° 56' N, 76°31' W), a 1485msnm, precipitación de 495mm durante el cultivo y temperatura promedio de 20°C, suelo inceptisol (Typic Dystrandept), pH 5,7 y 4,1ppm de P.

Genotipos de fríjol. Los 13 materiales en estudio son parte de la colección del banco de germoplasma que administra Corpoica y corresponden al acervo andino, de hábito arbustivo y de grano rojo, de las cuales, nueve son de Colombia: Diacol Andino, Antioquia 10, Antioquia 19, Antioquia 27A, Boyacá 18, ICA Cerinza, Cundinamarca 148, Línea 34400, Nariño 12 y cuatro son accesiones introducidas: México 496, México 497, Perú 40 y Perú 152 (Ligarreto, 2012) (Tabla 1).

Diseño Experimental. Los tratamientos corresponden a las 13 accesiones, distribuidas en un diseño de bloques completos al azar, con tres repeticiones. Las unidades experimentales contaron con un área de 9,6m², conformadas por 4 surcos de 4m de longitud, separados a 0,6m y con distancias entre plantas de 0,1m.

Análisis estadístico. La información registrada de rendimiento de grano fue procesada con el programa de estadística SAS® versión 9,0. Se empleó, para el análisis de varianza combinado de ambientes, el procedimiento GLM; se consideraron efecto fijo para el genotipo y efectos aleatorios del ambiente. El modelo estadístico lineal y aditivo para análisis combinado de varianza fue:

Yijk= µ + ρi +bj(i) +gk +(gρ)ik +eijk

Donde µ es la media general, ρi es el efecto aleatorio del ambiente, bj(i) es el efecto aleatorio de la repetición en la localidad, gk es el efecto fijo del genotipo, (gp)ik es el efecto aleatorio de la interacción genotipo por ambiente y eijk es el efecto aleatorio del error.

Para discriminar las accesiones de fríjol más estables, a través de los cinco ambientes, se emplearon los métodos estadísticos de Eberhart & Russell (1966) aplicando el software SAS®, como lo sugiere Ceballos (1998), el modelo Ecovalencia, de Wricke, (1962) y la Varianza de estabilidad, de Shukla (1972), como lo presentó Kang (1989) y efectos principales aditivos e interacción multiplicativa AMMI, programado en SAS, según lo descrito por Vargas et al. (1999).

RESULTADOS Y DISCUSIÓN

Al aplicar la prueba de normalidad de Shapiro Wilks a los residuales del modelo estadístico de la variable rendimiento, se encontró que hubo distribución normal y no fue necesario realizar normalización para analizar la estabilidad del rendimiento de los genotipos, a través de los cinco ambientes.

El análisis combinado de varianza, para rendimiento de grano en seco, a través de los cinco ambientes (A), presentó diferencias altamente significativas, para genotipos (G) y para la interacción GxA. Del total de sumas de cuadrados de los factores de variación, al efecto ambiente le correspondió un 69,3%; las repeticiones dentro de los ambientes, un 6,0%; al genotipo, 4,1% y a la GxA 9,41%. Datos similares a los reportados por Acosta-Gallegos et al. (2012), con 70,4% de la varianza para el efecto de ambiente y 11,8%, para la interacción GxA en estudios de adaptación de 16 genotipos de fríjol, en 15 ambientes de México.

Los ambientes más favorables para mayor rendimiento de grano fueron Mosquera 3 con 267mm de precipitación pluvial, durante el ciclo de cultivo y Darién, con precipitación de 495mm, mientras que los genotipos con mayor rendimiento promedio fueron Perú 40, que rindió 1147kg/ha, seguido por Diacol Andino y México 496, con respuesta diferencial de los genotipos a los ambientes, la cual, se puede explicar a través de los modelos de análisis de la interacción.

Análisis de GxA en el modelo de Eberhart Russell: En la tabla 2, se encuentran los índices de productividad ambiental y se muestra que el ambiente Darién fue altamente productivo, con un índice ambiental (ia) de 0,916. Esta localidad fue la de mayor precipitación, con 495mm durante el ciclo de cultivo, lo cual, unido al factor temperatura, con 20°C, permitió un mejor desarrollo de los genotipos, en relación a los ambientes de Mosquera, que presentaron menor precipitación, con deficiencias en los ambientes Mosquera 2 y, Mosquera 3 y estrés por sequía, en el ambiente Mosquera 4, que fue el menos productivo, con un ia de -0,83. En tanto, los ambientes Mosquera 1 y Mosquera 2 con ia=-0,253 y -0,288 afectaron, de manera negativa, el potencial productivo de los genotipos, sin presentar una diferencia marcada entre ellos. Estos resultados son equivalentes a los reportados por Vizgarra et al. (2012), en la separación de ambientes por respuesta para el germoplasma de fríjol, al presentar una elevada asociación con las lluvias y con la temperatura. El ambiente Mosquera 3 fue el mejor de los de clima frío, con potencial productivo de 1,38t/ha y una precipitación de 267mm, con oferta regular de siembra a cosecha del cultivo.

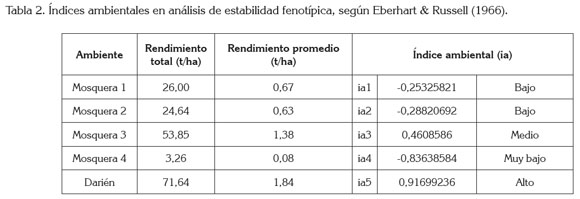
Respecto al coeficiente de regresión, con media ideal βi=1, se informa en la tabla 3, que las accesiones que presentaron βi=1 o estabilidad promedia fueron: Diacol Andino βi=1,012 e ICA Cerinza βi=1,111; Antioquia 10 βi=0,899 y Nariño 12 βi=0,878. Las accesiones de fríjol rojo arbustivo Antioquia 19, Antioquia 27A, Cundinamarca 148, L34400 y Perú 154 presentaron βi<1; tales genotipos mostraron una mejor capacidad en condiciones de mayores insumos, por lo tanto, son recomendados para sistemas de bajo potencial o con algún tipo de estrés; en este caso están adaptados a ambientes más fríos. Las accesiones de fríjol Boyacá 18, México 496, México 497 y Perú 40 presentaron estadísticamente βi>1; estas variedades son más sensibles a cambios ambientales y se pueden desarrollar mejor frente a ambientes con alto potencial productivo.

La consistencia del comportamiento de los genotipos en los ambientes con base en las desviaciones respecto a la regresión, está determinada por el segundo parámetro S²di, consignado en la tabla 3. Se encontró que la estabilidad de Diacol Andino es inconsistente, puesto que muestra en S²di=0,118 estadísticamente >0. La inconsistencia se puede explicar en una variación del rendimiento muy importante en ambientes similares (Márquez, 1976). En la tabla 2, se puede observar la gran variación que aportó el ambiente Mosquera 2 al sistema. El ambiente Mosquera 4, con estrés hídrico, fue el más desfavorable para los genotipos, en contraste con Darién, el cual, fue el de mayor potencial productivo.

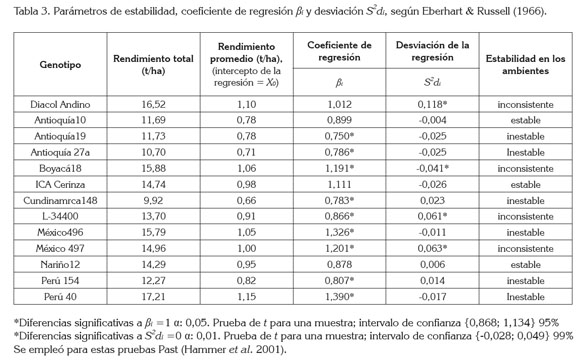
Los genotipos considerados estables y consistentes en su respuesta genotípica, dado que no hubo interacción con el ambiente de manera significativa con βi=1; S²di=0 son: ICA Cerinza, con S²di=-0,026; Antioquia 10 S²di=-0,004 y Nariño 12, S²di=0,006. Los genotipos Antioquia 19, Antioquia 27A, Cundinamarca 148 y Perú 154 tuvieron mayor resistencia a cambios ambientales, presentando interacción GxA alta y las desviaciones del rendimiento estadísticamente iguales cero (Tabla 3).

Los genotipos más sensibles a cambios ambientales y que respondieron consistentemente con altos rendimientos en ambientes de mejor potencial productivo y con una estabilidad inferior a la promedia (βi >1; S²di=0) fueron Perú 40 y México 496. En los casos donde la interacción GxA está expresada por ambos parámetros de estabilidad que tuvieron (βi>1; S²di>0), una buena respuesta a ambientes favorables, por una alta sensibilidad a cambios ambientales y menor estabilidad frente a la promedia, además, por una ligera significancia en la GxA, por desviación del rendimiento respecto a la regresión del modelo, fueron México 497 y Boyacá 18. El cultivar que presentó (βi <1; S²di<0) una inconsistencia en el rendimiento ejercida por las influencias ambientales, fue el L34400 (Tabla 3).

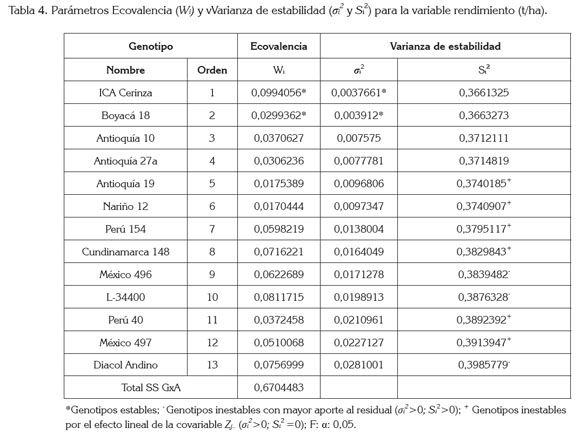
Modelo Ecovalencia Wricke y varianza de estabilidad Shukla: De acuerdo con Kang (2003), se utilizó el procedimiento IML (Interactive Matrix Language), para procesar matrices, utilizando promedios de los genotipos en los ambientes. La GxA fue significativa y se obtuvo una suma de cuadrados de 0,6704; al fraccionar las sumas de cuadrados de los genotipos en ecovalencia Wi y varianza de estabilidad σi2, se destacó el genotipo ICA Cerinza, como el más estable, por su menor aporte (Wi y σi2) a la suma total de cuadrados de la interacción GxA. Éste genotipo presentó un perfil más consistente, a través de los diferentes ambientes, gracias a una varianza (σi2) de estabilidad mínima, en referencia a los demás genotipos.

Contrario al análisis de Eberhart & Russell (1966), este procedimiento resaltó a la accesión Boyacá 18, como el segundo genotipo más estable con menor aporte a la GxA y un perfil cercano al de ICA Cerinza. En la tabla 4, aparecen ordenados los genotipos de menor a mayor, conforme a los criterios de Ecovalencia y varianza de estabilidad, en su orden: ICA Cerinza, Boyacá 18, Antioquia 10, Antioquia 27A, Antioquia 19, Nariño 12, Perú 154, Cundinamarca 148, México 496, México 497, L34400, Perú 40, México 497 y Diacol Andino. De acuerdo a Cruz (1992), la varianza de estabilidad σi2 significativamente diferente a 0 es un robusto estimador insesgado de la consistencia del rendimiento, a través de los ambientes, lo cual, permitió visualizar que tres de los 13 genotipos fueron muy inestables, en orden de mayor inconsistencia σi2 y mayor aporte al residual Si² de Shukla fueron: Diacol Andino, con superior aporte en la suma de cuadrados de GxA, Wi =0,895 o 14,84% de la suma de cuadrados GxA; σi2 =0,253 y Si² =0,309 diferentes de 0; L34400 con Wi =0,643 o 10,64% de la suma de cuadrados GxA; σi2=0,178 y Si²=0,242 diferentes de 0 y México 496 con Wi =0,561 o 9,29% de la suma de cuadrados GxA; σi2=0,154 y Si² =0,197 diferentes de 0.

Efectos principales aditivos e interacción multiplicativa AMMI: El modelo AMMI facilitó una proyección de la GxA por medio del Biplot, que es una ilustración robusta de la interacción en ejes sintéticos no correlacionados de máxima explicación, a partir de las variables de mayor peso. Estos nuevos ejes o componentes principales de la GxA, se evaluaron con la prueba de Gollob (1967), que determinó significancia en los primeros cuatro componentes principales (Cp). El primer Cp AMMI, presentó el mayor peso en la varianza, con un 43,75% y, el segundo un 35,56%, acumulándose en ellos 79,31% de porcentaje de varianza más relevante de la interacción GxA; se supone relevante mayor a, 75% de la explicación en AMMI según Crossa (1990) y Rodríguez et al. (2002) o mayor a 70%, según Hair et al. (1999). Vargas & Crossa (2000) mencionan que la prueba de Gollob es muy flexible, de modo que muchos términos AMMI puedan ser considerados significativos, pero en este caso, reduce eficientemente la variabilidad a los dos primeros componentes. La tabla 5, muestra los resultados del rendimiento promedio, las puntuaciones genotípicas y ambientales para los tres primeros términos AMMI.

La figura 1, muestra que el ambiente Darién (S5) presentó el mayor peso o carga factorial y está correlacionado de manera positiva con la GxA del CP1, a su vez, que fue el de mayor potencial en rendimiento para los genotipos. En la figura 1 aparecen las puntuaciones de los dos primeros componentes principales; el CP1 de la GxA es el mejor resumen de las combinaciones lineales que los datos manifiestan (Hair et al. 1999) y, una alta GxA, sugiere que los genotipos con mayor rendimiento en el estudio fueron las más inestables. Boyacá 18 tiene buena respuesta frente a estas condiciones, pero es uno de los genotipos considerados estables, por su ubicación cercana al centroide de la interacción (Figura 1). El ambiente Mosquera 2 (S2) es el segundo que aporta significativamente a la interacción GxA, por su variabilidad al CP1 (Figura 1), pero es de los ambientes con menor rendimiento respecto al promedio. Por otro lado, los genotipos cercanos al centroide son los de máximo potencial en todos los ambientes e irrelevantes a la GxA, en este caso, son ICA Cerinza y Boyacá 18, respecto CP1 del AMMI. Según la tabla 5, el ambiente Mosquera 3 (S3), es de buen potencial en rendimiento pero, no aportó significativamente a la GxA de los componentes principales 1 y 2. Este ambiente puede llegar a describir, con mayor certeza la respuesta, promedio de los ambientes.

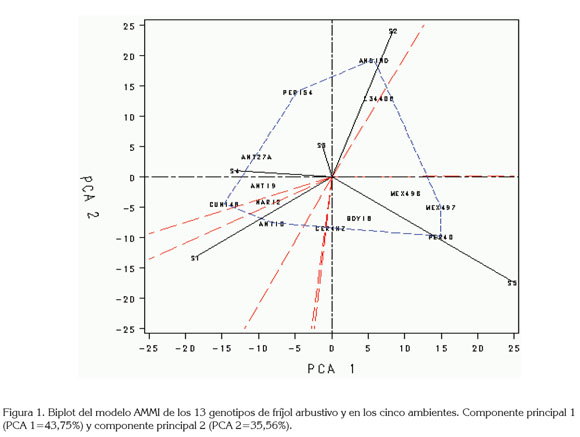
Los ambientes Mosquera 4 (S4) y Mosquera 1 (S1) están correlacionados negativamente con la GxA del componente 1, éste último con un mayor impacto.

En el biplot (Figura 1), los ambientes fueron agrupados en tres sectores: el primer sector reúne los ambientes de Mosquera 2 (S2), 3 (S3) y 4 (S4), en el cual, el Mosquera 2 (S2) fue el que mayor aportó a la GxA dada la magnitud de su vector. El segundo sector está comprendido solamente por el ambiente Darién, con el mayor aporte de todos los ambientes a la GxA y, en el tercer sector, contrastando al anterior, se ubicó el ambiente Mosquera 1 (S1). Estos sectores están representados por los ambientes que tienen mayor discriminación de las accesiones de fríjol.

El polígono del biplot describe a los genotipos que más respondieron a los estímulos ambientales, de manera positiva o negativa, dependiendo del signo y de la magnitud de la puntuación, fueron: Diacol Andino, México 497, Perú 40, Antioquia 10, Cundinamarca 148 y Perú 154. Según Vargas et al. (1999), en las proyecciones ortogonales, los vectores ambientales que tengan la misma dirección con los vectores de los genotipos tienen interacciones positivas, es decir, los ambientes son favorables para los genotipos, por tal razón, la variedad Perú 40, fue el genotipo que mejor respondió a los estímulos ambientales con buen desempeño en el Darién (S5).

Darién (S5) es un ambiente más propicio para establecer los genotipos de fríjol rojo tipo arbustivo: Perú 40, México 497 y México 496. El cultivar Cundinamarca 148 fue el del comportamiento más pobre en la mayoría de ambientes, debido a los bajos rendimientos y a la alta interacción GxA.

Los genotipos que mostraron adaptación en las condiciones del ambiente Mosquera 1 (S1) fueron en su orden: Antioquia 10 y Nariño 12. En el ambiente Mosquera 4 (S4): Antioquia 19, Antioquia 27A y Perú 154. En el Ambiente Mosquera 2 (S2), en su orden: Diacol Andino y L34400 respondieron muy bien. La estabilidad de ICA Cerinza es incuestionable en la serie de ambientes, porque se ubica en el centroide de la interacción y en el centro del macro-ambiente más discriminatorio para la GxA, conformado por el de mayor potencial Darién y, el de menor potencial el ambiente de Mosquera 1 (S1). Por su estabilidad y reducida interacción con el ambiente, es el genotipo recomendado comercialmente. Boyacá 18, también se consolidó como estable, por su colocación cercana al centroide y se puede adaptar muy bien a ambientes de altos rendimientos.

La respuesta diferenciada de los cultivares de fríjol en los ambientes generan la gran posibilidad para el sector productivo de utilizar materiales mejorados y recursos genéticos de variedades locales con buena estabilidad a los cambios medioambientales y de cultivares con buen comportamiento, para ambientes específicos.

En la interacción GxA para el método de Eberhart & Russell, los ambientes considerados con mayor potencial productivo fueron Darién y Mosquera 3, por los mayores rendimientos que presentaron los cultivares, siendo ICA Cerinza, Antioquia 10 y Nariño 12, los mas estables y Boyacá 18, inconsistente, en tanto que, en el modelo de ecovalencia de Wricke y varianza de estabilidad de Shukla, los genotipos de menor aporte a la GxA fueron ICA Cerinza y Boyacá 18; esta respuesta fue similar a la observada con el método AMMI.

Estos dos últimos métodos mostraron mayor robustez y sensibilidad respecto al comportamiento de la desviación, varianza y comportamiento de los genotipos en general.

Los genotipos con mayor rendimiento por hectárea no son necesariamente estables sino adaptables a ambientes específicos, como el caso de AMMI, que señalo a Perú 40 mejor acondicionado al ambiente Darién, que resulto ser el ambiente más favorable y discriminante para procesos de selección de los cultivares en estudio, a Diacol Andino en el ambiente Mosquera 2 y a Nariño 12 y Antioquia 10 en el ambiente Mosquera 1.

Agradecimientos: Los autores agradecen a la División de Investigación de la Universidad Nacional de Colombia, Bogotá y a Colciencias, por el soporte financiero, a través del proyecto "Evaluación y entrega al sector productivo de nuevas variedades mejoradas de fríjol y arveja con resistencia varietal para un desarrollo competitivo y sostenible en la región Andina". Conflicto de intereses: El manuscrito fue preparado y revisado con la participación de todos los autores, quienes declaramos que no existe conflicto de intereses que ponga en riesgo la validez de los resultados presentados.

BIBLIOGRAFÍA

1. ACOSTA-GALLEGOS, J.A.; ESPINOZA-TRUJILLO, E.; SÁNCHEZ-GARCIA, B.M.; JIMENEZ-HERNANDEZ, Y.; SALINAS-PEREZ, R.A.; ROSALES-SERNA, R.; ZANDATE-HERNANDEZ, R.; GONZALEZ-RIVAS, C. 2012. Adaptación del frijol tipo flor de junio a diferentes ambientes de México. Trop. Subtrop. Agroecosyst. 15:427-438.

2. ARIAS, J.; RENGIFO, T.; JARAMILLO, M. 2007. Manual de buenas prácticas agrícolas BPA en la producción de fríjol voluble. Convenio: FAO-MANA-CORPOICA Centro de Investigación la Selva. Gobernación de Antioquia, Colombia. Ed. CTP Print Ltda., Medellín. 167p.

3. CALDAS, G.V.; BLAIR, M. 2009. Inheritance of seed condensed tannins and their relationship with seed-coat color and pattern genes in common bean (Phaseolus vulgaris L.). Theor. Appl. Genet. 118:131-142.

4. CEBALLOS, H. 1998. Genética Cuantitativa y Fitomejoramiento. Impreso Universitario. U. N. Colombia. Palmira. 250p.

5. CROSSA, J. 1990. Statistical analyses of multilocation trials. Adv. Agron. 44:55-85.

6. CRUZ, R. 1992. Some exact conditional test for the multiplicative model to explain genotype - environment interaction. Heredity. 69:128-132.

7. EBDON, J.; PETROVICH, M.A.; ZOBEL, W.R. 1998. Stability of evapotranspiration rates in Kentucky Bluegrass cultivars across low and high evaporative environments. Crop Sci. 38:135-142.

8. EBERHART, S.A.; RUSSELL, W.A. 1966. Stability parameters for comparing varieties. Crop Sci. 6:36-40.

9. FINLAY, K.W.; WILKINSON, G.N. 1963. The analysis of adaptation in a plant breeding program. Australian J. Agr. Res. 14:742-754.

10. GAUCH, H. 1992. Statistical analysis of regional yield trials: AMMI Analysis of factorial designs. Elsevier Science Publishers. New York. 278p.

11. GOLLOB, H.F. 1967. A statistical model which combines features of factor analytic and analysis of variance techniques. Psycometrica. 33:73-115.

12. HAIR, J.F, ANDERSON, R.E.; TATHAM, R.L.; BLACK, W.C. 1999. Analysis Multivariante. 5a edición. Ed. Pearson Educación S.A. Madrid. p.98-121.

13. HAMMER, Ø.; HARPER, D.; RYAN, P. 2001. Past: Paleontological statistic Software Package for education and data analysis. Paleontología Electrónica, 4:1-9.

14. KANG, M.S. 1989. A new SAS program for calculating stability-variance parameters. J. Hered. 80(5):415.

15. KANG, M.S. 2003. Handbook of Formulas and Software for Plan Geneticist and Bredeers. 105 Sturgis Hall, Louisiana State University, Baton Rouge USA. Food Products Press. 124p.

16. LIGARRETO, G.A. 2012. Genetic diversity in a Colombian bean (Phaseolus vulgaris L.) collection as assessed by phaseolin patterns and isoenzymatic markers. Agr. Col. 30(2):179-187.

17. LYNCH, M.; WALSH, B. 1998. Genetics and Analysis of Quantitatve traits. Sinauer Associates, Inc. Publishers. Sunderland, Massachusetts. p.657-681.

18. MÁRQUEZ, S. 1976. El problema de la interacción genético ambiental en genotécnia vegetal. Universidad Autónoma de Chapingo. Departamento de Enseñanza, Investigación y Servicio en Fitotecnia. Editorial Patena, A. C., México D.F. 113p.

19. RODRÍGUEZ, J.; CASTELLANOS, J.; VILLASEÑOR, H.; MOLINA, J.; MARTÍNEZ, Y.A. 2002. Estabilidad de 7 variedades comerciales de trigo (Triticum aestivum L.) de temporal. Fitotecnia Mex. 25(2):143-151.

20. SHUKLA, G.K. 1972. Some statistical aspects of partitioning genotype-environmental components of variability. J. Hered. 28:237-245.

21. VARGAS, M.; CROSSA, J.; VAN EEUWIJK, F.; RAMÍREZ, M.; SAYRE, K. 1999. Crop breeding, genetics & cytology. Crop Sci. 39:955-967.

22. VARGAS, M.Y.; CROSSA, J. 2000. El análisis AMMI y la gráfica del Biplot en SAS. Universidad Autónoma de Chapingo. Unidad de Biometría y Estadística. CIMMYT, México D.F. México. 42p Disponible desde Internet en: www.cimmyt.cgiar.org/biometrics (con acceso 05/11/12).

23. VIZGARRA, O.; BEEBE, S.; MORALES, F.; BELLONE, C.; PLOPER, D. 2012. Interacción genotipo por ambiente en cultivares de poroto para el Noroeste Argentino. Rev. Ind. Agríc. Tucumán. 89(2):25-36.

24. WRICKE, G. 1962. Über eine Methode zur Erfassung der ökologischen Streubreite. Zeitschr. Pflanzenzüchtung. 47:92-96.

25. YATES, F.; COCHRAN, W.G. 1938. The analysis of group of experiments. J. Agric. Sci. 28:556-580.

26. ZOBEL, R.W.; WRIGHT, M.; GAUCH, H.G. 1988. Statistical analysis of yield trial. Agron. J. 80:388-393.

Recibido: Julio 22 de 2014 Aceptado: Febrero 17 de 2015

Revista U.D.C.A Actualidad & Divulgación Científica por Universidad de Ciencias Aplicadas y Ambientales se distribuye bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.