Ciencias de la Educación-Artículo Científico

UNA PROPUESTA METODOLÓGICA EN ETNOMATEMÁTICAS1

A METHODOLOGIC PROPOSAL IN ETHNOMATHEMATICS

Armando Aroca Araújo 2

1 La maestría que indica el resumen es en Educación, con énfasis en educación matemática, que ofrece la Universidad del Valle, Santiago de Cali, Colombia.

2 Licenciado en Matemáticas y Física - Universidad Popular del Cesar (UPC). Especialista en docencia para la Educación Superior, Universidad Santiago de Cali (USC). Estudiante de la Maestría en educación con énfasis en Educación Matemática, Universidad del Valle. Profesor tiempo completo de la USC y profesor hora cátedra Univalle. Dirección para correspondencia: Calle 62AN No. 2N-62, apartamento H-203, unidad residencial Bosques de Caranday, Santiago de Cali. Correo electrónico:aroca@etnomatematica.org,aaroca@usc.edu.co

3 Esta tesis de maestría se encuentra en el Centro de Documentación y Publicaciones, CENDOPU, de la Universidad del Valle.

Rev. U.D.C.A Act. & Div. Cient. 11 (1): 67-76, 2008

RESUMEN

En este artículo, se presenta la síntesis de una propuesta metodológica en etnomatemática producto de tres años de investigación, cuyo objetivo fundamental fue construir un plan de enseñanza de geometría para los indígenas arhuacos de la Sierra Nevada de Santa Marta, Colombia, teniendo presente el pensamiento matemático que se da en la práctica del tejido de las mochilas y su respectiva relación con su cultura e historia. El título del trabajo de investigación es "Una propuesta de enseñanza de geometría desde una perspectiva cultural. Caso de estudio: Comunidad indígena arhuaca. Sierra Nevada de Santa Marta"3. Esta metodología establece algunas pautas a tener en cuenta en el momento de escoger la bibliografía y el objeto de estudios etnomatemáticos y una forma de determinar el significado social y cultural de dicho objeto (indagación básica de la etnomatemática). Muestra también una manera de cómo se podría analizar matemáticamente dicho objeto y una forma general de transponer, didácticamente, los resultados de la investigación en contextos culturales distintos. En consecuencia, se presenta un camino de investigación para todos aquellos estudiantes de pregrado y postgrado e investigadores que estén interesados en la etnomatemática.

Palabras clave: Diversidad cultural, educación matemática, etnomatemáticas. análisis geométrico, mochilas arhuacas.

SUMMARY

This paper presents the synthesis of a methodological proposal in ethnomathematics as a result of three years of research, whose primary objective was to develop a plan for teaching geometry to the Arhuacos indians of the Sierra Nevada de Santa Marta, Colombia, taking into account the mathematical thinking which is included in the weaving of their "mochilas" and the relationship with their culture and history. The title of the research work is "A proposal for teaching geometry from a cultural perspective. Case Study: Indigenous Arhuaca Community. Sierra Nevada of Santa Marta, Colombia". This methodology provides some guidelines to take into account when choosing the literature and the objective of ethnomathematic studies, and a way to determine the social and cultural meanings of such an object (basic inquiry of ethnomathematics). It also shows a way of how such an object could be mathematically analyzed and a general form of transposing didactically these research findings in different cultural contexts. Accordingly, this research is a new alternative for undergraduate and graduate students and researchers who are interested in ethnomathematics.

Keywords: Cultural diversity, mathematics education, ethnomatematics. geometric analysis, traditional figures, Arhuacas knapsacks.

INTRODUCCIÓN

Las pautas metodológicas de investigación a describir darán una perspectiva de trabajo a todos aquellos estudiantes de pregrado y postgrado e investigadores interesados en la etnomatemática. Se debe precisar que el tema a proponer, referente a una comunidad indígena, no agota las diversas posibilidades de estudio que él tiene, pues la etnomatemática, interpretando a D’ambrosio (1985), es la matemática que desarrollan grupos sociales o culturales diferenciados entre sí. El mismo autor, quien es considerado el padre de la etnomatemática, a mediado de los años ochenta, acuñó el término con la siguiente composición: Etno: referente a grupos sociales y culturales diferenciados, matema: como las concepciones, ideas o conceptos (saberes) y ticas: como las diversas formas de hacer (prácticas). En la página web del ISGEM (International Study Group on Ethnomathematics), http://www.ccd.rpi.edu/Eglash/cbp/isgemsp.htm, se encuentra lo siguiente: el término, a veces se usa específicamente para las sociedades indígenas en pequeña escala, pero en su sentido más amplio el prefijo etno, se puede referir a cualquier grupo, sociedades nacionales, comunidades obreras, tradiciones religiosas, clases profesionales y así sucesivamente. Las prácticas matemáticas incluyen sistemas simbólicos, los diseños espaciales, técnicas de construcción práctica, métodos del cálculo, mediciones en tiempo y espacio, formas específicas de razonamiento e inferencia, y otras actividades cognoscitivas y materiales que se pueden traducir a representaciones de la matemática formal.

El desarrollo y el planteamiento de todo el proceso buscó responder a la pregunta ?cómo elaborar una propuesta de enseñanza de geometría transformacional que le permita al indígena arhuaco desplazarse desde la particularidad de algunas de las formas geométricas inscritas en su contexto cultural, hasta la generalidad de un sistema geométrico transcultural?

Los diseños que se tejen en las mochilas, llamados Figuras Tradicionales, fueron los escogidos, porque ellos son unos de los más fecundos en cuanto a desarrollo de pensamiento geométrico y simbólico. Los resultados del análisis permitieron generar una propuesta de enseñanza de geometría transformacional acorde con las exigencias teóricas de la comunidad indígena arhuaca.

Respecto a los antecedentes del trabajo de investigación, se desconocen qué trabajos etnomatemáticos se hayan realizado en Colombia, bajo este mismo enfoque metodológico.

MATERIALES Y MÉTODOS

Algunos detalles sobre el trabajo de campo:

Puesto que el enfoque etnomatemático que se escogió involucró la comunidad indígena arhuaca, la pregunta esencial fue ?cómo hacer un trabajo etnomatemático en una comunidad indígena colombiana? Aparte de los procesos de observación, las entrevistas, las centenares de fotografías y las decenas de dibujos que en su conjunto sirvieron para recoger información en diferentes sitios de la Sierra Nevada de Santa Marta y que todos ellos apuntaban a una aproximación de la lógica de construcción de las Figuras Tradicionales que se tejen en las mochilas arhuacas, hay cuatro situaciones que no se pueden desconocer en esta etapa: la primera hace referencia al objeto de estudio. En cuanto a su selección, las mochilas arhuacas se venden en grandes cantidades en locales comerciales y particularmente muchas de ellas son imitadas por mujeres descendientes de los extintos kankuamos, es decir, de ahí que cuando se trata de establecer una muestra confiable para el estudio, se debe ir al "centro" de la cultura. La segunda, los obstáculos del lenguaje: pretender que los términos técnicos de la matemática occidental sean entendidos por el grupo socioculturalmente diferenciado es un absurdo.; absurdo, no porque tales grupos no estén en capacidad de apropiarse tales términos, de hecho terminan por hacerlo cuando se los impone la educación actualmente impartida y absurdo, porque esta educación desnaturaliza y agrede su cultura autóctona. Cada uno de dichos grupos maneja sus propios términos, se trata, entonces, de que el investigador etnomatemático busque las prácticas y los saberes que le son de su interés. Tercera, todas las comunidades indígenas de América, desde la misma llegada de los españoles fueron sometidas a diversos procesos de explotación. En la actualidad, los indígenas de una u otra forma, al tener contacto por primera vez con cualquier investigador, lo asumen como alguien que trae unos intereses personales que implican cierta forma de explotación: "hacen plata con la cultura". Por último, las condiciones de seguridad: en la actualidad el trabajo de campo, tal vez en todas las zonas rurales de Colombia, implica algunos riesgos. Para las dos consideraciones anteriores, dos precauciones que podrían ser útiles son: sustentar con honestidad el proyecto ante las autoridades respectivas de la comunidad indígena (el cabildo, el consejo, el mamo, el cacique, un taita) y contar con su apoyo para el desarrollo de la investigación.

Sobre la selección del objeto de estudio etnomatemático:

Una de las preguntas básicas de una investigación etnomatemática es ?cuál es el significado social y cultural que tiene el objeto de estudio? Para más detalles sobre la esencia de esta pregunta se sugier consultar a Gerdes (1996); la complejidad de la respuesta implicaría la continuidad de la investigación. El mismo oficio es el gran indicador de una práctica y un saber diferenciados. Se trata de precisar qué de ese oficio se tomará como objeto de estudio. Es prudente establecer si esa práctica o saber tiene su propia historia, es decir, qué es lo híbrido desde lo cultural: qué ha incorporado la cultura occidental en ese oficio y qué es lo autóctono. En ese sentido, la práctica de tejer en las comunidades indígenas, se remonta a mucho antes de la llegada de los españoles, en consecuencia, hay certeza de que dichos saberes y prácticas, se desarrollaron por fuera de la influencia de las matemáticas occidentales.

En nuestro caso, se escogió como objeto de estudio el pensamiento que está congelado en el diseño de algunas Figuras Tradicionales y cuál es el significado cultural y social que dichas figuras tienen en la comunidad arhuaca. Se escogieron en total 16 de ellas y visualmente había indicadores claros que el tema de las transformaciones geométricas en el plano (traslaciones, rotaciones, reflexiones y deslizamientos), los frisos y algunos diseños bidimensionales, se podrían desarrollar. En este aspecto, se consultó a Alsina et al. (1989): ?cómo entonces se buscó el significado social y cultural del objeto de estudio escogido? Algunos de los fundamentos que se tuvieron en cuenta para clasificar la figura como tradicional fueron: 1) que gran parte de la comunidad la reconociera como tal y 2) que tuviera un soporte mitológico, es decir, como mínimo un mito que la soportara (las 16 figuras seleccionadas gozaban de ese grado de sacralización), pues el mito otorga al objeto mental o físico representado un grado importante de sacralización, pero es en el diseño donde se encuentra la mayor complejidad de sacralización al incorporarse completamente el simbolismo. Los mitos son los que mantienen vivos la tradición y la malla de significados que le da existencia a una comunidad indígena. En general, son los valores que le confiere el grupo al objeto escogido.

figura 1, muestra las 16 Figuras Tradicionales que se escogieron. Ella ha sido incluida en otros dos textos (Aroca, 2007a, 2007b). La importancia de esta figura radica en lo siguiente: 1) La organización de estas 16 Figuras Tradicionales implicó al rededor de un año de análisis y 2) esta clasificación probablemente inicie un debate en torno al nominalismo, cantidad, simbolismo y pertinencia de cada una de las figuras mostradas; esto traerá consigo una depuración de ellas y de paso un afianzamiento de la identidad cultural arhuaca y, por ende, del patrimonio cultural colombiano.

Al analizar diversas investigaciones en etnomatemáticas a nivel internacional, se puede establecer que hay tres formas básicas para hacerlo: 1) Analizar la lógica (matema) que se desarrolla en la práctica (tica) dentro de un contexto socio cultural (como investigador se llega desde afuera); en esta situación, el investigador etnomatemático encuentra el saber (matema) y la práctica (tica) en el grupo, por ejemplo, los diseños que se tejen en una mochila arhuaca. 2) Obtener esa lógica (matema) por medio de un estímulo externo, en este caso, la tica amerita sin duda atención, por la variación externa, pero estará mediada por el matema (pues son inseparables); nadie actúa sin una cosmovisión, una forma de pensar (matemas), actos espontáneos no existen, pues la cultura los media. 3) Establecer la tica, por medios de estímulos que representan los matemas del investigador. Esta última es lo que dio sentido a la etnomatemática, porque las escuelas están llenas de esta forma, el problema está en la mala aplicación, cuando se le quiere imponer un matema a otro (por ejemplo, a un grupo minoritario en una clase de matemáticas).

?Cuál fue el tratamiento que se le dio en la investigación a las Figuras Tradicionales seleccionadas? Se establecieron tres imágenes importantes relativas a cada una de ellas: 1) La imagen visual que el objeto muestra, que es más fácil de analizar si proviene del mundo físico que si proceden de la imaginación. Las Figuras Tradicionales que provienen del mundo de las ideas (objetos mentales) son: Serankwa, Kunsamana A’mía, Kunsamana Cheirua, Gamako y desde una perspectiva, Chinuzatu. Las demás, también incluyendo a Chinuzatu, imágenes que están relacionadas directamente con el mundo de los objetos físicos. Algunas imágenes son creaciones reproductoras de uno o de varios mitos. 2), la imagen que se encontró en la mochila y 3), la imagen que se tendrá que elaborar en el aula de clase a partir de la inclusión de los resultados del análisis de todas las figuras que se analizaron. En dicho análisis, se presentaron tres aspectos fundamentales: Análisis simbólico y de forma, en el que se explica el significado cultural o social de cada una de las Figuras Tradicionales, para demostrar que la representación en las mochilas es la que permite que un objeto se sacralice complejamente. También, se intentó mostrar la relación entre imagen y cosa representada; luego, se hizo un análisis geométrico que diera solución al problema de investigación y, como una fusión de los dos momentos anteriores, se concebió un paralelo comparativo en el que se buscaba justificar el porqué de cada trazo, considerando atentamente las condiciones propias que impone el hacer las figuras con una aguja (trenzado) en forma de espiral y limitada por completo de trazos curvos. Este análisis geométrico reveló tanto el patrón figural, dando una aproximación al patrón geométrico, característico de cada Figura Tradicional. Por patrón figural, se entiende el conjunto de trazos mínimos y visibles de la Figura Tradicional que permite, por medio de algunas transformaciones geométricas, generar toda la figura en sí. El patrón geométrico, que no es estrictamente mental, es la estructura del patrón figural, es el lenguaje formal que subyace a él, es el discurso que se trató de aproximar a la lógica de construcción de las mujeres arhuacas.

RESULTADOS Y DISCUSIÓN

Sobre el cuidado de la bibliografía a consultar:

Puesto que la etnomatemática se encuentra entre la historia de las matemáticas y la antropología cultural, cada vez que los educadores matemáticos o los matemáticos tratan de abordar las prácticas y los saberes matemáticos culturalmente diferenciados, manifiestan deficiencias, obstáculos o simplezas para analizarlos, pues terminan aplicando sólo su óptica profesional. Una investigación etnomatemática integra las dos visiones. Se precisa que fueron los antropólogos y no los matemáticos, quienes advirtieron sobre otras formas de ordenar, de contar, de medir. Para mayor conocimiento de este proceso, se puede consultar los trabajos citados por Gerdes (1996), tales como de Luquet (1929), Raum (1938), Fettweis (1881-1967), White (1947), Raymond L. Wilder, (1950, 1968, 1981).

Puesto que el objeto etnomatemático se vuelve de interés para la educación es allí donde aparece la pedagogía y la didáctica. Sin embargo, es factible que se pueda necesitar el apoyo de otras áreas, disciplinas o teorías, a parte de las ya descritas. En el caso particular, por los objetivos que el trabajo de investigación persiguió, éste se movió en un ambiente donde se trenzaron la antropología (etnografía), la arqueología, la geometría, la historia de las matemáticas, la didáctica y la cultura. El producto más importante de la investigación fue la elaboración de un texto que pretende establecer situaciones didácticas que apunten a la comprensión de la geometría (específicamente al tema de las transformaciones geométricas en el plano), con significado cultural, por parte de los estudiantes y profesores arhuacos.

De igual manera es prudente analizar otras metodologías investigativas en etnomatemáticas y teorías o sobre la educación matemática y su relación con la cultura. Para ello, se recomienda consultar la siguiente bibliografía: D’ambrosio (1985); Frankenstein & Powell (1997); Bishop (1999, 2005) y Blanco (2004). Si se desea tener una amplia visión de los trabajos en etnomatemáticas desarrollados en Colombia, se recomienda el artículo Blanco (2006). En el mismo sentido es prudente conocer la atmósfera que envuelve el objeto de estudio (bibliografía sobre el mismo objeto de estudio y el grupo cultural o social que lo produce); en el caso particular fue necesario revisar una significativa bibliografía sobre los arhuacos, entre la cual se puede citar a Orozco (1990), Reichel-Dolmatoff, (1991; 1951), De Vilanesa (1952), Usemi (1976), Rey (1994), Legast (1987), Castaño (1986), Torres et. al. (1997) y Arne (1986).

Sobre el análisis simbólico y matemático:

?Qué es un diseño simbólico en una comunidad indígena? La imaginación fecunda de las indígenas arhuacas, al momento de tejer sus mochilas, les ha permitido acercarse a la perfección de las figuras que tejen. Este ancestral proceso ha creado y fijado sus propios conceptos geométricos a favor de su propia identidad cultural. En este contexto, la geometría es una forma de pensamiento que preserva la identidad cultural y expresa su orden en un diseño simbólico que abarca tres niveles de significación del mundo: Cosmovisión: sobre el mundo físico, sobre el "entorno natural y social, representación de la iconografía natural"; cosmogonía: "que explica los orígenes y poderes de las entidades naturales, interpretando las concepciones mágicoreligiosas", y cosmología: "que expresa los conceptos de orden, número y ritmo, cohesionando lógica y orgánicamente a las concepciones del espacio una visión integral del todo y sus partes reflejado en la unidad de multiplicidad de la composición. ?Es como una forma de abstracción de las leyes de ordenamiento universal", Milla (1991). Estos tres planos de significación en el arte precolombino están representados también en las 16 Figuras Tradicionales que se consideraron y, por ende, no podrían estar por fuera de las posibles situaciones didácticas que implicaría la construcción de un texto de enseñanza de geometría transformacional.

A causa del proceso de deculturización de los arhuacos, dentro del grupo de las figuras citadas, hay algunas a las que se les denomina con significantes que no expresan, de acuerdo con la documentación histórica disponible, el significado ancestral de las Figuras Tradicionales. Interpretaciones simbólicas y análisis geométrico de las Figuras Tradicionales no se podían considerar por separado, tal como se hace en muchos estudios etnomatemáticos. Apostarle a este enfoque implica mayor esfuerzo investigativo pero es esencial si lo deseado es buscar una aproximación al significado social y cultural del diseño. En síntesis, la idea central fue establecer el nexo entre el objeto representado, su simbolismo, su forma y su geometría empleada.

Cuando se estableció el nexo entre esas dimensiones, la metodología utilizada en el análisis geométrico fue diversa, pues se trataba de determinar en las Figuras Tradicionales las perspectivas de construcción, es decir, cuáles son las transformaciones geométricas, frisos y diseños bidimensionales que la arhuaca usa al tejer la figura, a partir del patrón figural. En esta perspectiva, se tuvo en cuenta la propuesta metodológica propuesta por Albis (1986). Las n-uplas dieron cuenta de la estructura lógica del patrón figural, o sea, el patrón geométrico y el cual mostró el orden de cómo cada trazo aparece para constituir cada Figura Tradicional; en Gerdes (2003), se encontró esta metodología. De igual manera, se hizo una deconstrucción geométrica que consistió en la recreación visual, en detalle, de cómo va apareciendo cada trazo que da origen a cada una de las Figuras Tradicionales escogidas. Esa deconstrucción permitió encontrar el patrón figural, mostrar el proceso de construcción en sí, las transformaciones geométricas y otros procesos matemáticos. Para visualizar un patrón figural y un patrón geométrico, se recomienda mirar la figura 2. Para ver una deconstrucción geométrica de una Figura Tradicional, se recomienda ver la figura 3.

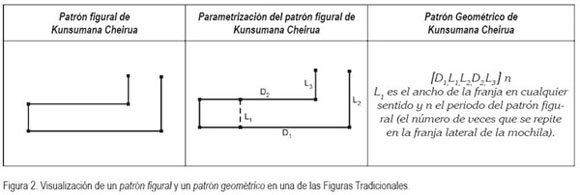
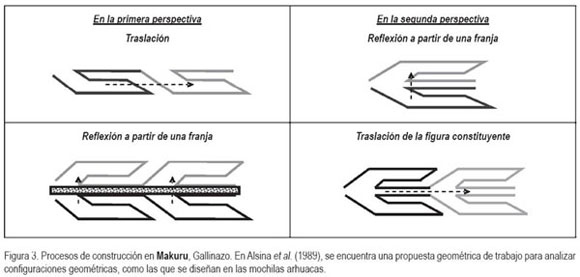
Como propuesta de discusión, el etnomatemático educador debe trascender el proceso descriptivo y buscar relaciones más complejas entre: a) Estructura geométrica, referente al pensamiento matemático que subyace a la configuración misma, b) representación figural, la simbología que está sujeta a cada configuración, c) sistema de símbolos, referente a las condiciones que permitieron que la cosa representada haya adquirido su sacralización y d) intervención cultural en el significado, relativo a que cuando una cultura ya no está encerrada en su sistema cultural, sino en intercambio continuo con una cultura hegemónica, se producen sistemas de representación simbióticos, híbridos.

La inclusión de los resultados en la propuesta educativa:

Como lo natural es que un estudio etnomatemático de esta naturaleza se apropie en la enseñanza, se hizo una propuesta educativa en geometría transformacional con los resultados de las fases anteriores, teniendo en cuenta las necesidades de la comunidad arhuaca. Los objetivos de la propuesta son los siguientes: 1. Conocer la lógica ancestral de pensamiento que utilizan las mujeres arhuacas al construir cada una de las Figuras Tradicionales. 2. Conocer formalmente los conceptos matemáticos occidentales que aparecen en el tejido de las Figuras Tradicionales. 3. Propender por desarrollar competencias matemáticas, cuyo formalismo le permita a los profesores y a los estudiantes indígenas concebir las matemáticas como un fenómeno intercultural, como una disciplina que hace y que ante todo explica problemas de la naturaleza. 4. Aportar al desarrollo metodológico propuestas educativas más acordes con las exigencias de la propia cultura. Estos objetivos de la propuesta no podían estar distantes de los objetivos generales que los indígenas arhuacos persiguen con respecto a su educación (Comité Educativo Arhuaco, 1986):

Los principios establecidos por los arhuacos, a manera de resumen, se muestran en la tabla 1. Por otro lado, se tuvieron en cuenta los cinco principios de la enculturación del currículo propuestas por Bishop (1999).

CONCLUSIONES

En este trabajo, se explica la metodología empleada en una de las primeras tesis de maestría en etnomatemática que se ha hecho en Colombia. Se trata, a partir de allí, de estimular la discusión sobre la educación matemática y la relación que tiene con el entorno cultural donde se desarrolla. Las matemáticas también están por fuera del salón de clases y las ideas o actividades que intervienen allí, tienen mayor significado social o cultural para los estudiantes que los mismos conceptos institucionales que la matemática occidental desarrolla. No se trata de una sublevación en torno a los conceptos institucionales, de algo complementario: se trata de responder a la pregunta ?de lo que se enseña de matemáticas para el estudiante qué tanto poder explicativo tiene de su entorno?

Por otro lado, en la medida que ésta es apenas una propuesta metodológica en etnomatemáticas, es igualmente importante el cuidado que se debe tener para no incluir la etnomatemática en una "jaula metodológica". Eso es, subordinar el investigador a la misma presión de las escuelas para imponer a otros una manera de investigar. La liberación metodológica es un tema de mucha importancia. Esta recomendación la debemos al profesor Ubiratan D’Ambrosio.

Colombia, es un país rico en diversidad cultural y social y, por ende, fecundo en formas diversas de pensar, de desarrollar y de aplicar las matemáticas. El caso de las configuraciones geométricas que las indígenas arhuacas tejen en sus mochilas es apenas un ejemplo de todo lo que hay por descubrir y llevar al currículo matemático. Estudiantes de pregrado y postgrados e investigadores en general pueden contribuir a la construcción de una política nacional sobre la enseñanza de las matemáticas, ligada realmente al contexto cultural.

BIBLIOGRAFÍA

ALBIS, V. 1986. Arte prehispánico y matemática. Revista de la Universidad Nacional (2da época). (Colombia) 2 ( 7): 29-34.

ALSINA, C.; PÉREZ, R. RUIZ, C. 1989. Bandas finitas. En: Matemáticas: Cultura y aprendizaje, SINTESIS eds. Simetría dinámica. Ed. Síntesis (Madrid). p. 83-92.

ARNE, R. 1986. Arhuaco. Sierra Nevada. Traducción de Gerda Schattenberg-Rincón. Ed. Ministerio de Cultura (Managua). 52p.

AROCA, A. 2007a. Análisis a una Figura Tradicional de las mochilas arhuacas. Artículo inédito. (Santiago de Cali). 15p.

AROCA, A. 2007b. Las tres partes de configuración geométrica de las mochilas arhuacas. Artículo inédito. (Santiago de Cali). 15p.

BISHOP, A. 1999. Enculturación matemática: La educación matemática desde una perspectiva cultural. Ed. Ibérica S.A. / Paídos, SAICF (Buenos aires). 239p.

BISHOP, A. 2005. Aproximación sociocultural a la educación matemática. Instituto de Educación y Pedagogía. Universidad del Valle. Ed. Merlín, I.D. (Santiago de Cali). 199p.

BLANCO, H. 2006. La etnomatemática en Colombia, un programa en construcción. Bolema ( Brasil). 26 ( 19): 42-72.

BLANCO, H. 2004. Educación matemática y etnomatemática. Compilación. Instituto de Educación y Pedagogía. Universidad del Valle. Texto inédito. (Santiago de Cali). 112p.

CASTAÑO, H. 1986. La mochila arhuaca, de su restauración y su conservación museológica. Escuela Nacional de Conservación, restauración y museología de Santa Clara. Ed. Instituto Colombiano de Cultura ( Bogotá). 60p.

COMITÉ EDUCATIVO ARHUACO. 1986. Hojas sueltas. ( Valledupar). 65p.

D'AMBROSIO, U. 1985. Socio-cultural bases for mathematics education. Unicamp. Centro de producciones (Campinas). 103p.

De VILANESA, Padre J. 1952. Indios arhuacos de la Sierra Nevada de Santa Marta. Descripción geográfica. Costumbres de los indios, idioma arhuaco. Ed. Iqueima ( Bogotá). 163p.

FRANKENSTEIN, M.; POWELL, A. 1997. Ethnomathematics: challenging eurocentrism in mathematics education (New York). SUNY Series, reform in mathematics education, State University of New York. USA. 440p.

GERDES, P. 2003. Níjtyubane - Sobre algunos aspectos geométricos da cestaria Bora na Amazónia peruana. Rev. Bras. História da Matemática. 3 ( 6): 3-22.

GERDES, P. 1996. Ethnomathematics and mathematics education. En ?Bishop, A.; Clements, K.; Keitel, K.J.; Laborde, C. (Eds). International Handbook of Mathematics Education. Ed. Kluwer Academic publishers (Dordrecht, The Netherlands). p. 909- 943

LEGAST, A. 1987. El animal en el mundo mítico Tairona. Ed. Banco de la República (Bogotá). 121p.

MILLA, Z. 1991. Introducción a la semiótica del diseño andino precolombino. Ed. Eximpress S.A. ( Perú). 92p.

OROZCO, J. 1990. Nabusïmake, tierra de arhuacos. Ed. ESAP - Centro de publicaciones ?( Bogotá). 387p.

REICHEL-DOLMATOFF, G. 1991. Los Ika. Sierra Nevada de Santa Marta, Colombia. Notas etnográficas. 1946 - 1.966. Ed. Centro Editorial Universidad Nacional de Colombia ?( Bogotá). 211p.

REICHEL-DOLMATOFF, G. 1951. Datos histórico - culturales sobre las tribus de la antigua gobernación de Santa Marta. Instituto etnológico del Magdalena. Ed. Banco de la República ( Santa Marta). 131p.

REY, J. 1994. Textiles de la Sierra Nevada de Santa Marta. Recopilación bibliográfica. Ed. 1. IADAP, Instituto andino de artes populares ( Quito). 73p.

TORRES, J.; ISQUIERDO, A.; AGUILAR, C. 1997. Zarinzuma amu'kwi anugwe terawa ikun niwi umuke zanu: Semillas, personales y corazones espirituales en arhuaco. Ed. Secretaría de Educación y Cultura Departamental (Valledupar). 85p.

USEMI: Unión de Seglares Misioneras. 1976. Tutu: Arte arhuaco. Ed. Usemi (Bogotá). 81p.

Recibido: Septiembre 27 de 2007 Aceptado: Marzo 4 de 2008

Licencia Creative Commons
Revista U.D.C.A Actualidad & Divulgación Científica por Universidad de Ciencias Aplicadas y Ambientales se distribuye bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.