CIENCIAS SOCIALES Y ECONÓMICAS - Artículo Científico

PENSAMIENTO GEOMÉTRICO EN LAS MOCHILAS ARHUACAS

GEOMETRIC THOUGHT IN THE ARHUACAS KNAPSACKS

Armando Aroca Araújo¹

¹Licenciado en Matemáticas y Física ? Universidad Popular del Cesar (UPC). Especialista en docencia para la Educación Superior ? Universidad Santiago de Cali (USC). Magister en educación con énfasis en Educación Matemática ? Universidad del Valle (Univalle), Dirección para correspondencia: calle 62N No. 2AN-68, barrio los Alamos. Apto H-203. Santiago de Cali, Valle del Cauca, Colombia. Correo electrónico:aaroca@usc.edu.co,aroca@etnomatematica.org.

Rev. U.D.C.A Act. & Div. Cient. 11(2): 71-83, 2008

RESUMEN

La mochila arhuaca es un objeto precolombino fecundo en belleza y desarrollo de pensamiento geométrico ancestral. Por esa riqueza serán tres las perspectivas de análisis que presenta este artículo, ante la complejidad de los diseños que le dan configuración y atavío a ella: 1. Se hace relación al desarrollo de pensamiento geométrico-simbólico, que se establece al elaborar la mochila arhuaca. 2. Se presenta un análisis detallado de los procesos etnomatemáticos que se incorporan al tejer las figuras tradicionales en la parte lateral de la mochila, luego un análisis de las gasas y, por último, un análisis de los diseños que se muestran en los fondos de las mochilas, que se divide a su vez en tres categorías: fondos que definen espirales, fondos que definen anillos concéntricos y aquellos que combinan anillos concéntricos y figuras tradicionales. 3. Se presentan algunas reflexiones sobre los aportes educativos que podría dar la etnomatemática que las mujeres arhuacas desarrollan en las mochilas; estas tienen que ver, entre otras, con la importancia del color a la hora de desarrollar pensamiento geométrico. La inexactitud que hay en las medidas y sus consecuencias similares, en cuanto al desarrollo de conceptos geométricos escolares.

Palabras clave: Mochilas arhuacas, etno-matemáticas, análisis geométrico, educación, etno-educación.

SUMMARY

It is the arhuaca knapsack a fertile pre-colombian object in beauty and development of ancestral geometric thought. Due to its wealth, three are the perspectives of analysis presented in this article, in the presence of the designs complexity that provides them configuration and beauty: 1. Reference is made about the development of the geometric-symbolic thought when elaborating the knapsack. 2. A detailed analysis of the ethno-mathematic processes which are incorporated when knitting the traditional figures of the lateral part of the knapsack is presented, next an analysis of the gauzes is made and, finally, an examination is realized of the designs shown in the bottoms of the knapsacks, divided into three categories: bottoms that define spirals, those that define concentric rings and those that combine concentric rings and traditional figures. 3. Some reflections on the educational contributions of the ethno-mathematic developed by the arhuacas women in the backpacks are presented; these have to do, among others, with the importance of the color when developing geometric thought, and with the inaccuracy that exists in the measures and their similar consequences towards the development of similar scholar geometric concepts.

Key words: Arhuacas knapsacks, ethno-mathematics, geometric analysis, education, ethno-education.

INTRODUCCIÓN

Dieciséis Figuras Tradicionales que se tejen en las mochilas arhuacas.

Es difícil encontrar en la comunidad indígena arhuaca, comunidad residente en la Sierra Nevada de Santa Marta de Colombia, un objeto distinto a sus mochilas que atrape y armonice cultura, estética y pensamiento matemático. Lo importante en ellas no es su interpretación ornamental, es la diversidad de ideas geométricas ancestrales que se visualizan gracias al color-forma, que es empleado para dar forma a una figura tradicional. Todo este pensamiento es desarrollado por la mujer arhuaca. ?Qué es una figura tradicional? Es un diseño que cumple ciertas condiciones: 1) Cualquier mujer a cierta edad la puede tejer, 2) es reconocida como tal por gran parte de la comunidad, 3) tiene simbolismo que está relacionado con objetos físicos o mentales, 4) su estética se da en la puntada apretada y minuciosa y la conjugación de colores vivos o parcos (el color-forma) y 5) tiene congelado un pensamiento matemático que le da estructura y que le confiere a la figura representatividad. Estas conclusiones fueron aportes, en algunos casos, de mamos y mujeres arhuacos.

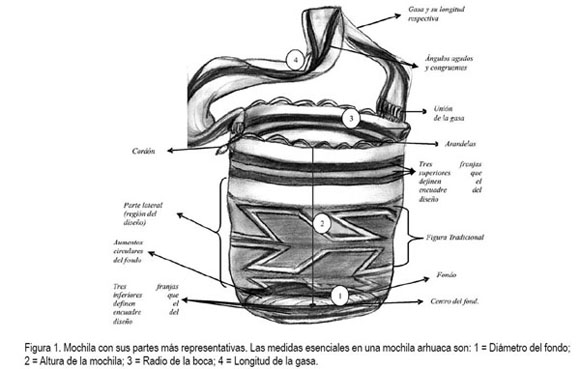
Los procesos de simetría, fundamentalmente, transformaciones geométricas en el plano, que al parecer tienen estrecha relación con la división ritual de la Kankurwa (la casa sagrada), son los que generan admiración visual, es decir, esa apreciación estética genera un pensamiento, porque hay un diseño ancestral que produce orden y, en este caso, lo causa la aplicación de procesos geométricos que se construyeron por fuera de la matemática escolar. Dichos procesos pertenecen a lo que se podría denominar el patrimonio matemático local, que es transferido de generación en generación, de una madre a sus hijas. Ese pensamiento matemático interviene en cada una de las dimensiones esenciales de una mochila arhuaca: número de puntadas, diámetro del fondo, longitud de la gasa, radio de la boca y altura de la mochila (número total de vueltas). Estas dos últimas son fundamentales para determinar el periodo del patrón figural, es decir, cuántas veces se repite horizontalmente la figura mínima, que sirve, a partir de procesos repetitivos de tejeduría, para hacer la figura tradicional. La figura 1, muestra los parámetros básicos de una mochila arhuaca, cuya figura tradicional es Kanzachu.

Interpretando a las indígenas arhuacas entrevistadas, cuyo proceso se realizó en Valledupar o en las estribaciones sur occidental o sur oriental de la Sierra Nevada de Santa Marta, muchas figuras que se tejen en la actualidad son producto de la imaginación de la tejedora o exigencias del comprador. Esto implica variación en los patrones figurales, cambios en el orden y hasta pérdida gradual del patrimonio matemático que ellas manejan de otrora; en otras palabras, las variaciones de los patrones geométricos de los diseños pueden implicar también una derrota a la permanencia del simbolismo que identifica la cultura de los arhuacos.

Respecto a la relación simbolismo y geometría, se puede analizar que si un diseño tiene simbolismo entonces puede tener una configuración geométrica, y puede ir desde una transformación simple hasta una que incorpore diseños bidimensionales. En la mochila arhuaca está impresa y expresada la cosmovisión, la cosmogonía y, con mayor fuerza, la cosmología que los arhuacos tienen de su mundo; es decir, los tres niveles de significación del mundo (Milla, 1991). La mochila al ser un objeto simbólico mediado por la abstracción geométrica es también una extensión de esa concepción, esto toma mayor fuerza, al saber que las indígenas arhuacas adquirieron de su entorno físico y de sus mitos algunos referentes que fueron sacralizados mediante figuras tradicionales, dando así una connotación diferente de otros: aquellos que fueron sacralizados, sólo por el mito, carecen de un nivel más representativo que es la visualización (figura 1 en Aroca, 2008).

La palabra geometría no existe en el lenguaje de los arhuacos y ellos al usarla la dicen en español. Las etno-matemáticas, término establecido por Ubiratan D?Ambrosio, en entrevista con Blanco (2008), muestran que muchas culturas del mundo le han dado un significado distinto a la geometría. Su etimología fue enseñada en occidente como geo = tierra y metría = medición, medición de la tierra; para el caso de los arhuacos, la palabra debe ser contextualiza. El mismo espacio sagrado tiene medidas simbólicas y Orozco (1990) así lo explica: ?Aunque la creación del mundo en espiral sugiere la figura del cono como imagen de la Sierra, no obstante, la imagen del mundo que tienen los arhuacos es la de pirámide de base cuadrada y compuesta por cuatro pisos, la que además tiene su correspondiente simétrico hacia abajo, que será también otra pirámide de cuatro pisos?. El concepto de medida comporta significaciones diferentes para referirse a la situación que ocupa en el espacio el individuo y su comunidad. En los arhuacos la ?geometría? es como un pensamiento al servicio de la identidad cultural.

Por otro lado, existen apuntes de cronistas españoles que Reichel-Dolmatoff (1951) sistematizó, donde se da cuenta de las prácticas de espartería y cestería de los Tayronas y de la descripción de esta actividad e información sobre el tejido de algunas figuras de animales. Por su parte, Vilanesa (1952) afirma lo siguiente: ?Todos los arhuacos usan la mochila como un complemento de su vestido. Las figuras representan animales totémicos: escorpiones, arañas, búhos, sapos, serpientes y leones?. De esto, existe una gran coincidencia entre las observaciones de aquellos cronistas y Vilanesa, que hace pensar que a pesar de la brusca desaparición de los tayronas y consecuente aparición de los arhuacos, varias de sus prácticas sociales no desaparecieron y permanecen hasta el día de hoy. En este sentido, deberían permanecer los patrones geométricos que se utilizan para la elaboración de dichos diseños. A manera de hipótesis, se podría plantear que, ante la invasión simbólica de una cultura, lo más resistente en una cultura local, son sus patrones geométricos diseñados comunitariamente y es por eso que, independientemente, de la materia prima utilizada, las formas se parecen y se identifican en contextos distintos. Por ejemplo, en Castaño (1986), se encuentra lo siguiente: ?La lana de oveja apareció en el siglo XIX traída por los españoles y fue reforzada por la Misión Capuchina a principio del siglo XX, quienes aumentaron la cantidad de ovejas?, luego ?la lana acrílica, o sintética, apareció en la segunda mitad del siglo XX, llevada por la comercialización e industrialización de la época moderna?. Y en este tiempo, los diseños permanecieron, es decir, que los patrones geométricos resistieron.

MATERIALES Y MÉTODOS

Para obtener los resultados, se procedió así: Las figuras están constituidas por fotografías, dibujos o gráficas hechas por el autor. La figura 1, fue un dibujo elaborado a principios del año 2008, basado en una de las mochilas del autor; la figura 2, muestra fotografías de gasas tomadas en Valledupar, en la Casa Indígena, en Pueblo Bello y en Nabusímake y el proceso para las fotos de la figura 3 fue similar. Los otros fondos, fueron dibujos hechos en Nabusímake y en Valledupar. En algunos casos, se diseñaba rápidamente un croquis y algunos parámetros que luego se reproducían. Fueron alrededor de 100 dibujos que se hicieron entre fondos, gasas y figuras laterales; se tomaron alrededor de unas 200 fotos. Las gráficas de la tabla 1, que se hicieron en el 2007B, son copias de las figuras tradicionales clasificadas en la Figura 1, en Aroca (2008). Para las gráficas de la tabla 2 y para la figura 4, se empleó el Cabri2plus_142_Spanish.exe. Para poder obtener datos, como medidas angulares y longitudes, se usó un transportador y una regla. La observación, sin duda alguna, fue una herramienta esencial para obtener varias imágenes y conclusiones, se realizó en los lugares ya descritos más en un almacén y una residencia (en el sector conocido como ?El Boliche?), en el centro comercial de Valledupar, que frecuentan los indígenas arhuacos. Todas estas actividades se hicieron entre los años 2005 y 2006. Algunos de los datos obtenidos no hubiesen sido posibles obtenerlos sin la colaboración de varios y varias indígenas arhuacos.

RESULTADOS Y DISCUSIÓN

Las tres partes de configuración geométrica en la mochila arhuaca

La figura 1(Aroca, 2008) y las figuras 2 y 3 muestran las tres partes de configuración geométrica de una mochila arhuaca: la parte lateral, la gasa y el fondo. Por ejemplo, en la parte lateral de la mochila, no es posible hacer trazos curvos, en cambio en los fondos la curva si es posible. En la gasa solo se tejen ángulos agudos que muestran una congruencia entre sí. Después de definido el fondo, se procede a la elaboración del tejido de la parte lateral, que se teje en forma ascendente en espiral continua o fraccionada, siempre de izquierda a derecha. Fraccionada quiere decir, que según sea la figura tradicional, se puede ir tejiendo partes repetitivas de la figura. Entre ellas, se deja un espacio que es rellenado después. La congruencia de los ángulos agudos u obtusos, se obtiene mediante los conceptos ?muy largo? o ?muy corto? en segmentos (última fila de la tabla 1). En el análisis geométrico no es posible dejar de lado el color, el cual, se asume como forma y no como ornamento. El color juega un papel muy importante para captar los patrones en una configuración. El color también da ritmo, sus combinaciones y alternancia proporcionan configuración, estructura. Él posibilita el análisis geométrico y es como un mapa que devela saberes ancestrales. No se puede tejer una figura tradicional si no se incluyen, al menos, dos colores. En el diseño no hay pensamiento geométrico si no hay un juego de colores.

Las perspectivas de construcción en la parte lateral

Varias de las transformaciones geométricas en el plano, se encuentran en la construcción de las figuras tradicionales, empleadas para dar ritmo, estética a la figura diseñada y representar la identidad cosmológica. La forma de dividir un recinto sagrado puede influir en la configuración de un diseño; en consecuencia, los actos de diseño son regidos a partir de la concepción de orden que tiene la cultura. Entonces, bajo la perspectiva de las transformaciones geométricas básicas en el plano, se puede dar una muestra de esas ideas geométricas que las arhuacas construyeron sin influencia externa. La figura 1, en Aroca (2008) presenta 16 figuras tradicionales de ese desarrollo ancestral de ideas geométricas.

?Cómo las arhuacas consiguen las transformaciones que se muestran en la tabla 1?

1). Ellas cuentan con dos unidades de medida que son la puntada y la vuelta. Por ejemplo, si en una vuelta de una mochila existe un trazo de n puntadas, simplemente, se vuelve a tejer sea por medio de una traslación, una reflexión, un deslizamiento, entre otros y es así como se consigue la simetría. Dicha medida se puede hacer usando los dedos o por medio de la observación. 2). En los arhuacos, su concepción de equilibrio, se refleja en la necesidad de incorporar la simetría y es por eso que si se teje un ala de un ave en movimiento, la perspectiva de diseño será aquella que refleje la otra. 3). Una vez más se valida que el desarrollo de pensamiento matemático se hace en todo contexto cultural. Bishop (1999) estableció las seis prácticas universales que generan pensamiento matemático (contar, medir, explicar, jugar, localizar y la concreta para este tema, diseñar), es decir, la geometría euclidiana no es universal. Lo universal son las prácticas que generan pensamiento matemático y sus similitudes que se encuentra entre las prácticas descritas. Alsina et al. (1989) establecen que en el friso se reconoce el orden y la periodicidad y que además, ellos, son patrimonio de todas las culturas. Reforzando aún más que las matemáticas son un producto cultural.

Construcción en las gasas

La gasa, se hace por separado y mediante un entrecruces de hebras de varios colores, en el cual, el primer dedo del pie (el gordo) sirve de soporte para elaborarla. El punto medio de la extensión de la gasa, por lo general, lo determina la distancia que media entre el codo y la mano. Llama la atención observar que del manejo complejo de estas hebras, salga una sucesión alternada de ángulos, prácticamente, congruentes en su amplitud.

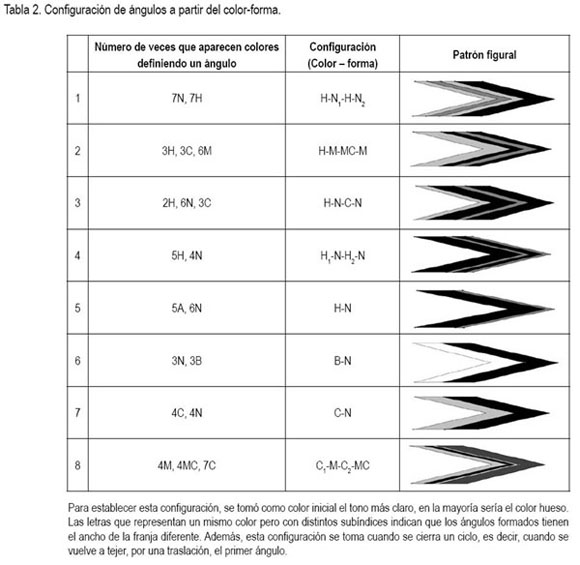
En las gasas de las mochilas arhuacas no simplemente ?hay ángulos?; en esa banda geométrica, el color-forma juega un papel esencial a la hora de establecer procesos de configuración. Algunos detalles de las gasas, que muestra la tabla 2, sirven para hacer generalizaciones: los colores que más se emplean al utilizar lana de oveja, son: hueso (H), negro (N), marrón (M), cenizo (C), marrón claro (MC) y blanco (B). También, se puede incorporar una variedad significativa de tonos al usar el maguey teñido con tintes artificiales o naturales o usando lana sintética. En la tabla 2, se nota una muestra de la variabilidad que las arhuacas pueden usar con los ángulos, todos agudos, en un rango que podría oscilar entre 15° y 40°. Para este caso, el concepto de ángulo no se puede asumir como porción del plano determinado por dos semirrectas con origen común sino como un par de segmentos de franjas de igual color que tienen dos de sus extremos comunes y que siempre forman un ángulo interno agudo; a estos se les llamará ángulos gruesos. Lo que se pudo observar es que no había más de cuatro ángulos gruesos diferentes en una gasa. No se podría decir que la mínima cantidad es uno, porque en la gasa 7 de la tabla 2, se encontraría un contraejemplo, suponiendo que exista un color que sirva de plano de construcción, ?cuál sería el ángulo en dicha gasa? En consecuencia, las configuraciones (el patrón figural), se forman con dos, tres y cuatro ángulos gruesos y una amplia variabilidad respecto al ancho de las franjas que los definen. Sin duda, el ancho (aproximadamente 7cm) y el largo (aproximadamente 81cm) de la gasa establecen límites de configuración; en este sentido la columna No. 2 de la tabla 2 estable valores concretos. Este espacio es suficiente para que la mujer arhuaca desarrolle pensamiento geométrico. En la gasa también se puede notar una línea central, producto de los cortes transversales que se forma en los entrecruces; esa es la referencia para que converjan allí cada par de vértices de cada ángulo grueso, así la congruencia en su amplitud puede llegar a ser perfecta.

Construcción en los fondos

El ancho del fondo (aproximadamente 21cm de diámetro), se mide en ocasiones con la mano abierta y su tejido se hace en forma de espiral horizontal. En esta parte de la mochila, se pueden tejer trazos curvos que generan anillos concéntricos o se puede hacer visible la misma espiral, como lo muestran las fotos y de la figura 3. Las formas que en los fondos se tejen estarían dadas por tres grupos: 1). El que define espirales. 2). El que define anillos concéntricos y en este grupo, se podría pensar en dos clasificaciones: uno que solo define anillos concéntricos (Fotos ?₂₁ , ?₂₂ , ?₂₃ , ?₃₂) y otro que combina anillos con círculos (Fotos ?₁₃ , ?₃₁ , ?₃₃ , ?₄₁ , ?₄₂ , ?₄₃). 3). El que define combinaciones entre el grupo 2 y las figuras tradicionales (Fotos ?₅₁ , ?₅₃). Es el grupo de mayor complejidad en el diseño. Usemi (1976) presentó otros fondos, pero no se pudieron encontrar en las más de 300 mochilas que se fotografiaron o dibujaron.

Fondos que definen espirales

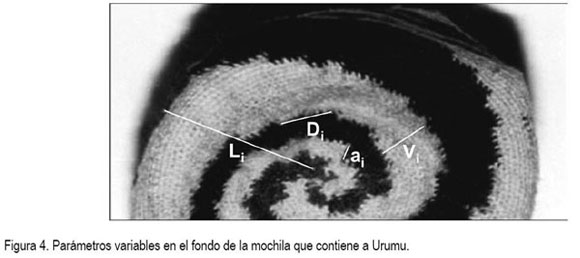
Si hay un fondo que define, a partir del color-forma, una espiral es porque en la parte lateral de la mochila está Urumu (Caracol, la concepción del tiempo arhuaco). Es en la única figura tradicional que pasa esto. En Urumu, la mujer arhuaca encuentra la posibilidad de tejer ?curvas?, mediante una poligonal que se le aproxima por escalonamiento y lo puede conseguir, teniendo en cuenta que entre menos aumente las puntadas verticales puede conseguir el trazo curvilíneo, sea en el fondo o en la parte lateral, pero debido a que la superficie del trabajo de tejeduría es significativamente pequeño, no puede construir curvas muy cerradas sino abiertas. En una cara de la mochila no es fácil que pueda tejer de un momento a otro una curva, tal vez por dos razones: es más fácil tejer trazos rectos, debido al sistema de técnicas que se emplea y la demanda de tiempo y dos, por el conocimiento mismo de la tejeduría que es ancestral y paradigmática. En la construcción de Urumu, en la región lateral de la mochila, los trazos horizontales tienden a tener dos distancias de separación homogéneas, lo cual, permite el ascenso en espiral. Cosa distinta sucede en el fondo, allí la distancia de separación es creciente, pues el ancho de la espiral viene abriéndose. Aquí se muestra que hay dos miradas: una en el fondo de la mochila, donde se teje en espiral pero definiendo una región circular, mientras que, en la parte lateral, se teje en espiral pero definiéndose una superficie cilíndrica; esto hace que la visión no abarque por completo la figura y habrá entonces que pensar cómo el ojo puede captar el ascenso en espiral en dicha superficie, eso, precisamente, lo logran las dos distancias de separación descritas (se describen como a_i y D_i). La figura 4 muestra algunos parámetros que son esenciales en la construcción de la espiral en el fondo de la mochila. Si a_i es muy pequeña, por ejemplo, tres vueltas y D_i está alrededor de 30 puntadas, se genera una sensación de franja curva.

Algunas características importantes de Urumu son: 1). Es la única figura tradicional que empieza desde el fondo. 2). Los parámetros de construcción en el fondo son completamente variables, en cambio, en la parte lateral, tienden a ser constantes. 3). En la parte lateral el número de vueltas a_i siempre es pequeño, oscila entre dos y cinco vueltas regularmente. 4). El punto inicial de a_i en el borde superior de la franja tiende, por lo general, a ser la puntada media de D_i en el borde inferior de la misma franja. 5). El número de vueltas V_i, que contribuye a generar el ancho ascendente en la parte lateral tiende a ser constante, aunque en el fondo es creciente. 6). En el fondo de la mochila tanto a_i como V_i son completamente variables y crecientes. 7). Hay un aumento progresivo de la distancia D_i a medida que se aleja del centro de la base y tiende a ser constante cuando llega a la parte lateral de la mochila. 8). A medida que el patrón figural se aleja del centro del fondo todos sus parámetros aumentan y tienden a ser constantes tan pronto tocan el borde inferior de la parte lateral de la mochila. 9). El color-forma juega un papel reflexivo en este grupo: del centro de la base puede arrancar un par de franjas de colores diferentes y cada par de estas franjas tienden a tener comportamientos simétricos entre sí. También, se puede dar un comportamiento simétrico hasta tres espirales distintas. 10). El inicio es un poco confuso; en promedio, después de las diez primeras vueltas, la franja define sus tres parámetros fundamentales D_i, V_i y a_i . 11). La franja avanza circularmente en espiral. 12). El aumento de V_i, a medida que se va acercando al borde inferior de la parte lateral de la mochila tiene un progresivo crecimiento que depende de la distancia de dicho borde al centro de la base, o sea, ‌V_i‌ = kL_i , donde k es una constante de proporcionalidad.

Fondos que definen anillos concéntricos

Algunas características de estos fondos son: 1). Hay relación de la configuración del fondo con el patrón figural de la gasa, la diferencia está en su forma. 2). Si se toma el punto central del fondo, a manera de un centro de homotecia, se podría notar que los anillos siempre aumentan su perímetro y con respecto a su ancho, existen tres posibilidades: se mantienen constantes, crecen o decrecen y esto lo indica el color-forma. Es posible no encontrar anillos sino un solo círculo o un círculo central y luego uno o varios anillos. No se supone que se puedan encontrar círculos concéntricos, pues esto lo restringe el color-forma.

Fondos que combinan anillos concéntricos y figuras tradicionales

Algunas características de este grupo son: 1). Las pocas figuras tradicionales que se incorporan en este grupo son alrededor de cuatro, principalmente, Makuru o parte de él. 2). Los ángulos que se forman al dividir los 360° del fondo en partes similares, pueden ser pequeños o grandes, o sea,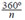 donde n es el número de veces que se repite circularmente la figura tradicional en la región angular, por lo general, en la franja externa o central circulares de dicha región; esto se conoce también como un grupo de simetrías (Foto ?₅₁, de la figura 3). 3). Todas las figuras tradicionales incorporadas juegan un papel de movimiento circular en torno al centro, confiriéndole así movimiento a la espiral que determina el fondo y, de paso, reafirmando la concepción del tiempo en los arhuacos. 4). Todas estas configuraciones se realizan ?mirando? directa o indirectamente el centro del fondo de la mochila, el proceso de construcción tiene en cuenta todo el círculo de construcción, pero de una u otra forma también el centro, el ombligo del mundo.

Algunos aportes educativos desde la perspectiva etnomatemática

Sobre estas prácticas y saberes que se desarrollan en el tejido de las mochilas arhuacas, que además son parte del patrimonio matemático colombiano, se podrían tener en cuenta algunos aspectos o conceptos que probablemente tendrían algún aporte educativo.

Geometría de las aproximaciones

Todas las magnitudes equivalentes en ua figura tradicional no son iguales, son aproximadamente iguales. Las culturas indígenas no buscan regirse por la exactitud; la rigidez de la geometría escolar aquí no existe. Su interés no radica en construir ángulos o lados congruentes, es decir, que las transformaciones geométricas que se realizan en las mochilas arhuacas no mantienen exactamente las medidas, pero sí casi la forma y el tamaño. El concepto de paralelismo y perpendicularidad que tienen las arhuacas les permite hacer los procesos anteriores. En esto se nota, claramente, que los instrumentos culturales juegan un papel destacado para construir las ideas. Las arhuacas nunca utilizan reglas para trazar líneas rectas en las mochilas. La ?linealidad? de las puntadas radica en que una de ellas, seguida de la otra, muestra, representa y da la imagen de esa idea de línea que hay en la mente de la tejedora. Esta geometría de las aproximaciones estaría clasificada en una inexactitud horizontal por puntada y una inexactitud vertical por vuelta.

La línea como optimizadora de formas

Se ha insistido que en la franja lateral de las mochilas no se tejen curvas, no en el fondo de ella. Para sortear su carencia, se recurrió a la línea para representar los objetos físicos y mentales. Esto obliga a que se tejan tres tipos de líneas: vertical, oblicua aproximada (izquierda o derecha) y horizontal que en conjunto generan paralelismo, perpendicularidad, transversalidad y franjas quebradas. Con el paralelismo dan grosor, anchura y hasta variación al objeto representado que lo incorpore. Por ejemplo, Háku es construido a partir de rectas oblicuas que se bisecan entre sí, lo cual, forma rombos. Kunsumana Cheirua y Kunsumana A?mía son desarrolladas solo en función de un paralelismo quebrado.

Un pensamiento geométrico fecundo de cosmología y significado cultural

Los arhuacos consideran el mundo lleno de equilibrios: la lluvia sigue a la sequía; los cuatro niveles de arriba del nivel medio le dan forma reflexiva a los cuatro niveles inferiores del mundo. Esta cosmología está plasmada en la configuración geométrica de las figuras tradicionales, todas y cada una de las puntadas están guiadas por ella. Esto desde un orden del universo ya preestablecido, a partir de la misma creación del mundo, cuando Kako Serankwa lo concibió y Urumu le dio su forma. Cada puntada está saturada por una carga simbólica poderosa: cada figura geométrica, cada patrón figural están ligados a una creencia y sólo pueden ser expresadas mediante el colorido. Estas formas mentales toman su significación de la entidad física que las representaría, que es, a su vez, una construcción cognoscitiva.

Sin color, no hay desarrollo de pensamiento matemático en el diseño de las mochilas arhuacas.

Sin más de un color, en el tejido de las mochilas arhuacas, no hay desarrollo de ideas geométricas diferentes a las que se pueden generar al tejer solamente la forma de la mochila; en este sentido, el color no es ornamento, es forma. El color codifica y recrea formas mentales de objetos. Con el color existe otra manera de hacer geometría. El color-forma fue la herramienta escogida por las mujeres arhuacas para plasmar sus esquemas mentales culturales que la mitología ya había sacralizado. ?Por qué las mujeres arhuacas y no las arzarias y las kogi pudieron desarrollar todos estos procesos complejos si los tres grupos cuentan con los mismos recursos? Valdría la pena investigar con mayores detalles para dar una respuesta.

Los posibles estragos al patrimonio matemático colombiano

Todos estos saberes y prácticas descritos hacen parte del patrimonio matemático colombiano. De ahí su importancia. Pero también es real que todas las comunidades indígenas están siendo sometidas por la cultura dominante que tengan como vecina. Esto se ve reflejado en las configuraciones geométricas que vienen desarrollándose desde tiempos remotos. En la actualidad, la arhuaca prefiere tejer mochilas, cuyos diseños sean rápidos y progresivamente ha dejado a un lado a aquellos diseños que estimulen y desarrollen un pensamiento geométrico significativo.

BIBLIOGRAFÍA

ALSINA, C.; PÉREZ, R.; RUÍZ, C. 1989. Bandas finitas. En: Simetría dinámica. Matemáticas: Cultura y aprendizaje. Ed. Síntesis. Cap. 4, (Madrid). p.83-92.

AROCA, A. 2008. Una propuesta metodológica en etnomatemática. Rev. U.D.C.A Actualidad & Divulgación Científica. 11(1):67-76.

BISHOP, A. 1999. Enculturación matemática: La educación matemática desde una perspectiva cultural. Ed. Ibérica S.A. / Paídos, SAICF (Buenos Aires). 239p.

BLANCO, H. 2008. Entrevista al profesor Ubiratan D?Ambrosio. Rev. Latinoamericana de Etnomatemáticas. (Pasto). 1(1):19-23. Disponible desde Internet en http://etnomatematica.org/v1-n1-febrero2008/blanco.pdf (con acceso 05/06/08).

CASTAÑO, H. 1986. La mochila arhuaca, de su restauración y su conservación museológica. Escuela Nacional de Conservación, restauración y museología de Santa Clara. Ed. Instituto Colombiano de Cultura (Bogotá). 60p.

MILLA, Z. 1991. Introducción a la semiótica del diseño andino precolombino. Ed. Eximpress S.A. (Perú). 92p.

OROZCO, J. 1990. Nabusïmake, tierra de arhuacos. Ed. ESAP ? Centro de publicaciones (Bogotá). 387p.

REICHEIL-DOLMATOFF, G. 1951. Datos histórico ? culturales sobre las tribus de la antigua gobernación de Santa Marta. Ed. Banco de la República. Instituto etnológico del Magdalena. (Santa Marta). 131p.

USEMI: Unión de Seglares Misioneras. 1976. Tutu: Arte arhuaco. Ed. Usemi (Bogotá). 81p.

VILANESA, Padre J. de. 1952. Indios arhuacos de la Sierra Nevada de Santa Marta. Descripción geográfica. Costumbres de los indios, idioma arhuaco. Ed. Iqueima (Bogotá). 163p.

Recibido:Agosto 4 de 2008; Aceptado: Octubre 20 de 2008