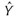CIENCIAS AGROPECUARIAS Y BIOLÓGICAS - ARTÍCULO CIENTÍFICO

ESTIMACIÓN DEL ÁREA FOLIAR DE PAPAYA (Carica papaya L.) BASADA EN MUESTREO NO DESTRUCTIVO

ESTIMATION OF PAPAYA (Carica papaya L.) LEAF AREA BASED ON NON-DESTRUCTIVE SAMPLING

Carlos Cardona Ayala¹; Hermes Araméndiz Tatis²; Carlos Barrera Causil³

¹ M.Sc. Universidad de Córdoba, Grupo de Investigación en Cultivos Tropicales de Clima Cálido, carrera 6 N° 76-103, Montería, Córdoba. E-mail: ccardona@sinu.unicordoba.edu.co

² Ph. D. Universidad de Córdoba, Grupo de Investigación en Cultivos Tropicales de Clima Cálido, carrera 6 N° 76-103, Montería, Córdoba. E-mail: haramendiz@hotmail.com

³ Estadístico. Universidad de Córdoba, Facultad de Ciencias Básicas e Ingenierías, carrera 6 N° 76-103, Montería, Córdoba. E-mail: cbarrera03@gmail.com;carlosbarrera@itm.edu.co

RESUMEN

El cultivo de papaya (Carica papaya L.) es muy importante en la fruticultura del departamento de Córdoba, por la buena calidad de la fruta producida. La investigación, se realizó en Montería, a 13msnm, temperatura media de 27.4°C, precipitación anual de 1346,1mm, humedad relativa de 84%; y brillo solar anual de 2180,2 horas, con el fin de obtener un modelo que permita estimar el área foliar de la planta, a partir de muestreo no destructivo. Mediante muestreo aleatorio simple, se seleccionaron hojas sanas de plantas adultas, de diferentes tamaños y distintas etapas de desarrollo, de los doseles superior, medio e inferior, de la variedad Maradol roja. Se tomaron medidas longitudinales: largo y ancho máximo de la hoja, ancho de la hoja a un medio, un tercio, un cuarto, un quinto y dos tercios de su largo, ancho máximo de lóbulos y longitud de nervadura de los mismos, con la finalidad de determinar las medidas altamente relacionadas con el área fotosintética de la hoja. El área foliar (Y), se midió por el método de relación peso: área, sobre una muestra de 30 hojas por dosel. Se construyeron modelos de regresión simple y múltiple, para luego seleccionar el de mejor ajuste. Se seleccionó un modelo de regresión simple, cuya variable explicativa corresponde a la longitud de la nervadura central del lóbulo izquierdo, contiguo al adyacente lóbulo medio (X). El modelo ajustado resultó ser: 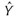= -303,0742 + 31,2028X, R² = 0,9335.

Palabras clave: Papaya, estimación área foliar, Maradol roja, modelos de regresión.

SUMMARY

The papaya (Carica papaya L) is a very important crop in the Cordoba state, especially for the good fruit quality. This research was carried out at Montería at 13masl, 27.4°C, annual rainfall of 1346.1mm, 84% relative humidity and 2180.2 hours annual sunlight, in order to obtain a model to estimate the plants leaf area, based on non-destructive sampling. A probability sampling procedure was used to select different size leaves and developmental stages from the upper, middle and lower canopy of adult plants of the red Maradol variety. Maximum leaf length and width, width of the middle third, fourth, fifth and two-thirds of leaf length, lobe width and midrib length of every lobe were registered with the purpose of identifying measures highly related to photosynthetic leaf area. The leaf area (Y) was measured based on the weight:area relation, from 30 leaves per canopy sample. Simple linear regression models and multiple linear regression were adjusted. A simple linear regression model was selected which independent variable representing the length of the midrib, next to the left next lobe and adjacent to the middle lobe (X). The adjusted model was: 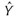= -303,0742 + 31,2028X, R² = 0,9335.

Key words: Papaya, leaf area estimation, red Maradol, regression models.

INTRODUCCIÓN

El cultivo de papaya es muy importante en la fruticultura del Departamento de Córdoba y Colombia, especialmente, por la buena calidad de la fruta. En el departamento de Córdoba, durante el período 1992 – 2006, fueron plantadas 2133ha, donde se destaca el municipio de Valencia, con 896 hectáreas, con un rendimiento de 21t·ha^-1, un volumen de producción de 44958t y una participación del 27%. En el contexto nacional, se ubica como el segundo productor (Agronet, 2008).

La papaya es un fruto de sabor agradable, de alto valor nutritivo por ser fuente excelente de vitamina C, con alto contenido de fibra y folato, conocido como vitamina B9, requerida para la producción de glóbulos rojos normales, además de ser un gran auxiliar para la digestión; la papaya roja también es rica en Vitamina A (Anuario Estadístico de Veracruz, 2001).

Las hojas, en conjunto, constituyen el órgano más importante de la planta y juegan el papel principal en las actividades anabólicas por medio de la clorofila, que poseen en abundancia, único medio para los procesos fotosintéticos. El área foliar total, que ha sido directamente relacionada con la cantidad de clorofila, es un parámetro importante para estimar la habilidad de la planta para sintetizar materia seca (Campostrini & Yamanishi, 2001).

El área foliar es uno de los parámetros más significativos en la evaluación del crecimiento de las plantas; su adecuada determinación durante el ciclo del cultivo posibilita conocer el crecimiento y el desarrollo de la planta, la eficiencia fotosintética y, en consecuencia, la producción total de la planta (Teruel, 1995; Costa, 1999). Así mismo, ayuda en la definición de la época ideal de siembra y de transplante: si no se tienen en cuenta otros factores, los cultivos deben ser sembrados en ciertas épocas, en las cuales, el máximo valor de índice del área foliar coincida con la época de elevada radiación, cuando la fotosíntesis líquida sea máxima (Galvani et al. 2000). De igual manera, sirve para estimar las necesidades hídricas de los cultivos (Allen et al. 1997), por lo que se requieren modelos matemáticos sencillos y rápidos, para su estimación (Guo & Sun, 2001; Arjona, 2003).

Se ha propuesto que las mediciones de los incrementos del área foliar y su duración ofrecen un método alternativo para estimar el potencial fotosintético de las plantas. Recientes estudios y modelaciones de las interacciones entre los regímenes dinámicos de radiación y el desarrollo de las hojas, en conjunto, se han enfocado sobre la interceptación total de la energía radiante, como un factor predictor de la producción de materia seca (Campostrini & Yamanishi, 2001).

Los métodos directos de medición de área foliar están restringidos al uso de equipos automáticos costosos; el empleo de planímetros resulta muy tedioso y, en algunos experimentos, el tiempo es insuficiente para realizar tales mediciones (Manivel & Weaver, 1974). La estimación del área foliar a través de modelos matemáticos, con mediciones directas en las hojas, es bastante preciso, económico y no destructivo (Blanco & Folegatti, 2003).

Un modelo matemático es una simplificación del sistema real y consiste en una ecuación o juego de ecuaciones, las cuales, representan cuantitativamente las hipótesis acerca del sistema real. Estos modelos, se emplean en muchos campos y, a través de ellos, se han hecho simulaciones y elaborado ecuaciones, para facilitar las mediciones en el crecimiento de las plantas cultivadas (Thornely, 1976; Bidwel, 1984; Elser & Jubb, 1988; Kingston & Van Epenhuijsen, 1989; Montoya et al. 1991).

El desarrollo de modelos matemáticos a partir de medidas lineales de una lámina foliar para predecir su área fotosintética, se ha usado en diversos estudios de crecimiento y de desarrollo de diferentes especies (Montoya et al. 1991; Gamiely et al, 1991); algunas de las medidas más comunes tenidas en cuenta en las ecuaciones de estimación son: longitud de la hoja, ancho de la hoja, longitud del pecíolo, diámetro del pecíolo o combinaciones entre estas variables.

El modelo matemático puede ser obtenido por correlación entre la longitud de la hoja (L), ancho (W) o longitud por ancho (LW) de área foliar (LA) de una muestra de hojas, a través del análisis de regresión. Los métodos no destructivos, se fundamentan en mediciones lineales que son rápidas, fáciles de medir y permiten una buena precisión, en estudios de crecimiento de muchas especies vegetales (Manivel & Weaver, 1974; Sepaskhah, 1977; Chirinos et al. 1997; Guo & Sun, 2001; Arjona, 2003; Blanco & Folegatti, 2003; Espitia et al. 2006).

La papaya es una fruta posicionada en el mercado nacional y con prospectiva de exportación, debido a que el país posee condiciones de clima, suelo y tecnológicas que lo permiten y el mercado de importaciones hacia Estados Unidos, cada día es más creciente (Anuario Estadístico de Veracruz, 2001), lo cual, hace necesario contribuir al desarrollo del cultivo como sistema de producción eficiente, ya que su conocimiento permite estar atento al crecimiento y desarrollo de la planta y, en consecuencia, a su manejo agronómico en aspectos asociados a las necesidades hídricas, programación de planes de fertilización, para reducir costos y ser mucho más competitivos en la producción. Por lo tanto, el presente objetivo fue obtener un modelo matemático para estimar el área foliar, con la toma de medidas directas de las hojas en campo, sin emplear el muestreo destructivo.

MATERIALES Y MÉTODOS

El estudio, se realizó en condiciones de campo y de laboratorio en la Universidad de Córdoba (Montería-Colombia), ubicada a una altura de 13msnm, con coordenadas geográficas de 8° 48'de latitud Norte y 75° 52' de longitud Oeste, en un bosque seco tropical, según la clasificación de Holdrige, con precipitación anual de 1346,1mm, temperatura media del aire de 27,4°C, humedad relativa de 84% y brillo solar anual de 2108,2 horas (Palencia et al. 2006).

Se llevó acabo un muestreo aleatorio simple para la selección de hojas, se tomaron diferentes tamaños, en diferentes etapas de desarrollo de las plantas de un cultivo establecido con la variedad Maradol roja, sembrada a 3m, entre plantas y 2,6m, entre hileras, a partir de los 45 días después del transplante. Esta variedad es de porte bajo, precoz en el inicio de floración, frutos de tamaño mediano, agradable sabor y susceptible a antracnosis.

La determinación de las variables o medidas de las hojas relacionadas con el área foliar, se hizo sobre una muestra de 30 hojas, de cada uno de los doseles, superior, medio e inferior de plantas adultas, determinados por altura, seleccionando hojas sanas de distintos tamaños. Después del muestreo, las hojas se conservaron en un recipiente térmico con hielo y transportadas al laboratorio, localizado a 10km del cultivo comercial.

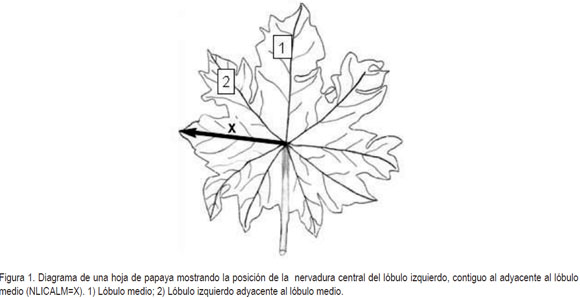
Se efectuaron mediciones, con una regla milimetrada, de la longitud de la nervadura central del lóbulo medio (NLM), longitud de la nervadura central del lóbulo izquierdo, adyacente al lóbulo medio (NLIALM), longitud de la nervadura central del lóbulo derecho, adyacente al lóbulo medio (NLDALM), longitud de la nervadura central del lóbulo izquierdo, contiguo al adyacente al lóbulo medio (NLICALM) y longitud de la nervadura central del lóbulo derecho, contiguo al adyacente al lóbulo medio (NLDCALM); como variable dependiente el área Foliar (AF).

El área foliar, se obtuvo por el método de relación peso: área o del “sacabocado” de 2,30cm de diámetro (área=4,1548cm²), el cual, es explicado de la siguiente manera: a cada hoja de la muestra se le determinó su masa fresca, extrayendo seis discos de tejidos de cada lámina foliar, luego, se obtuvo la masa fresca de cada uno y se halló la media y el coeficiente de variación de los discos (Pire & Valenzuela, 1995). Seguidamente, se calculó el área foliar de cada hoja, a través de la relación entre el peso fresco y el área unitaria del disco, así:

El análisis de las relaciones entre las medidas de las hojas y el área foliar se hizo mediante correlación simple y múltiple, con el fin de extraer información sobre el grado de asociación lineal entre las variables área foliar y las medidas lineales de las hojas.

Se aplicó el paquete estadístico SAS versión 9.1 (SAS, 2007) para la construcción y la selección de los modelos, mediante la técnica ”STEPWISE” (regresión paso a paso), la cual, tiene como criterio de selección el R2 máximo y una prueba de significancia F o un estadístico Cp. Se construyeron y se ajustaron modelos de regresión simple y múltiple; al seleccionado, se le realizaron las respectivas validaciones de los supuestos.

El método de regresión paso a paso o por pasos, consiste en construir, de manera iterativa, una secuencia de modelos de regresión, mediante la adición o eliminación de variables en cada paso. El criterio para añadir o eliminar una variable en cualquier paso, se expresa de manera fácil, en términos de una prueba parcial F.

La regresión por pasos comienza al formar un modelo con una variable que utiliza la variable de regresión que tiene la correlación más grande con la de respuesta y ésta también es aquella de regresión que produce el estadístico F más grande. En general, en cada paso, se examina el conjunto de variables de regresión restantes y se introduce la que tenga el estadístico parcial F más grande, siempre que sea posible. Este procedimiento continua hasta que se alcanza una etapa, en la cual, no se pueden insertar variables adicionales o no se les puede eliminar (Montgomery & Runger, 1996; Rawlings et al. 2001)

El estadístico Cp es también una herramienta para la selección del modelo. Cp es definido como:

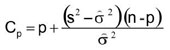
Donde p es el número de parámetros en el modelo; s², el cuadrado medio del error para el modelo candidato y , una estimación de la varianza poblacional σ². Son deseables valores pequeños de Cp (Walpole, 1995).

Las pruebas más comunes sugeridas por la literatura estadística se emplearon para la validación de los supuestos del modelo: normalidad de los errores (prueba de Shapiro Wilk), heteroscedasticidad de los errores (prueba de White), independencia de los errores (prueba de Durbin Watson), aleatoriedad de los residuos (prueba de rachas o de secuencias) y diagnóstico de multicolinealidad, con la prueba de multicolinelidad, basada en la estructura la estructura de la matriz X'X, que se puede escribir como X'X = VD²V',donde V es una matriz ortogonal, cuyas columnas son los vectores propios de X'X, y D², una matriz diagonal de valores propios asociados a los vectores propios correspondientes (Gujarati, 1997; Rawlings et al. 2001).

RESULTADOS Y DISCUSIÓN

Significancia del modelo y sus parámetros: El análisis de regresión con el PROC REG y el proceso de selección de las variables predoctoras, mediante la técnica STEPWISE o paso a paso del programa estadístico SAS permitieron seleccionar, como variable independiente, la longitud de la nervadura central del lóbulo izquierdo, contiguo al adyacente al lóbulo medio (NLICALM). La prueba F del análisis de varianza resultó altamente significativa (p>F = 0.0001), entonces, el área foliar (AF=Y) está relacionada linealmente con la longitud de la nervadura central del lóbulo izquierdo, contiguo al adyacente al lóbulo medio (NLICALM = X) (Figura 1; Tabla 1). Además, esta variable explica la variación del área foliar (AF=Y) en un 93,35%, es decir, R²=0,9335 y tiene un valor de la estadística Cp= 0,2987, considerado pequeño, de acuerdo con los criterios de selección del modelo (Walpole, 1995).

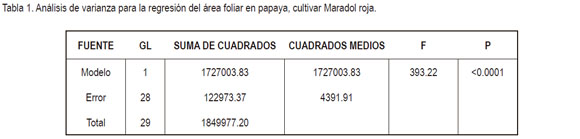
El modelo de mejor ajuste resultó ser:

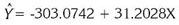
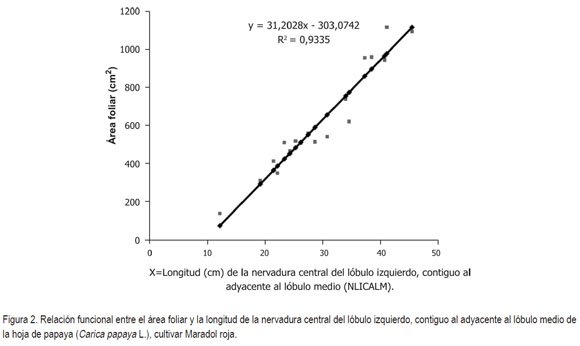
Según la ecuación estimada, con un error estándar de 1,573cm, por cada centímetro que se incremente la longitud de la nervadura central del lóbulo izquierdo, contiguo al adyacente al lóbulo medio (NLICALM = X), el área foliar aumenta en 31,2028cm², con efecto lineal (Figura 2, Tabla 2).

Este resultado difiere con respecto al estudio de Campostrini & Yamanishi (2001), quienes estimaron un modelo único para cuatro genotipos de papaya (Sunrise Solo 72/12, Sunrise Solo T J, Tainung 02 y Know-You 01); cuando utilizaron la medida directa de la longitud de la nervadura central del lóbulo medio, obtuvieron un modelo logarítmico, con un coeficiente de determinación de 0,898.

La línea de regresión estimada sólo es válida dentro del rango de valores de X, es decir, que no es conveniente extrapolar el uso de la línea para otros valores, pues la forma de la respuesta puede cambiar fuera de este rango. Así, los valores encontrados de medidas lineales de la nervadura del lóbulo izquierdo, contiguo al adyacente al lóbulo medio (NLICALM = X) de las hojas de papaya oscilaron entre 12,1 y 45,4cm, valores comunes en la especie, según la etapa de desarrollo de la hoja.

Se debe anotar que , intercepto cuyo valor en el modelo es de -303,0742 cm², no tiene interpretación práctica; sólo es un término de ajuste que permite representar la tendencia de los datos (en el espacio de valores observados para la variable independiente), mediante un modelo de línea recta. Para que sea posible una interpretación de es necesario que sea físicamente posible que X tome el valor de cero y, además, que se hayan recolectado datos con X=0, lo cual, es imposible cuando se trata de medir el área foliar.

Por otra parte, la variación del coeficiente de regresión es pequeña, toda vez que el área foliar sufre incrementos entre 27,98 y 34,43 cm², por cada centímetro de longitud de la nervadura central del lóbulo izquierdo, contiguo al adyacente al lóbulo medio (NLICALM = X), afirmación respaldada por un coeficiente de confianza de 0,95 (Tabla 2).

Es claro que un modelo o ecuación que permite estimar el área foliar es de gran utilidad práctica, cuando se trata, por ejemplo, de evaluar el efecto de las distintas condiciones estresantes, de común ocurrencia en los sistemas de producción agrícolas. Tales condiciones, como las relacionadas con el estrés biológico, causado por artrópodos plaga y enfermedades criptogámicas, se manifiestan en disminuciones de área foliar por daño directo sobre las hojas o inducción de senescencia precoz de las mismas (Hidalgo et al. 2006). Es evidente, además, que bajo estrés hídrico los rendimientos también se reducen, como consecuencia de la pérdida de área foliar (Ribas et al. 2000).

Es en estas situaciones que un modelo matemático es de gran utilidad, puesto que constituye una herramienta para estimar ¿qué tanto está disminuyendo o aumentando el área foliar total? y ¿cómo influye en los rendimientos? Así, los ensayos de aplicación de biocidas, de fertilizantes, de riego y de otras prácticas agronómicas, se pueden evaluar, con la ayuda de modelos matemáticos, aplicando los diseños experimentales o de muestreo apropiados.

Por otra parte, la estimación del área foliar, también es de gran utilidad cuando se trata de ajustar poblaciones de plantas para obtener el índice de área foliar crítico (IAF crítico), o sea, aquel que intercepta el 95% de la radiación incidente con el consecuente aumento significativo de la tasa de crecimiento del cultivo (TCC). En la medida en que el IAF aumenta, la TCC también lo hace, hasta que el dosel intercepta el 95% de la radiación incidente. Por encima de un IAF crítico, la TCC no incrementa significativamente (Monteith, 1965; Squire, 1990).

Cumplimiento de los supuestos del modelo: Al verificar el supuesto de independencia de los errores (e) por medio de la prueba de Durbin-Watson, se obtuvieron los puntos de significancia de dLy dUpara n= 30, un nivel de significancia de 0,05 y una variable explicativa.

El valor de la estadística de Durbin Watson es:

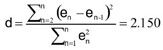
Ahora, como 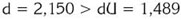, se tiene que d es significativo, por tanto, se rechaza la hipótesis nula al nivel de significancia α= 0,05; de aquí, se concluye que los errores no están autocorrelacionados, sino que son estadísticamente independientes, y por lo tanto, el modelo estimado cumple con el supuesto del análisis de regresión que establece que el error estándar de estimación es independiente para cada valor de la variable explicativa, esto es, la longitud de la nervadura central del lóbulo izquierdo, contiguo al adyacente al lóbulo medio (NLICALM = X).

Para la prueba de normalidad, el estadístico de la prueba de normalidad de los errores de Shapiro-Wilk, obtenido por medio del PROC UNIVARIATE NORMAL de SAS, mostró que evidentemente los errores se distribuyen normalmente.

Se tiene que 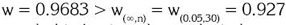, por tanto, se acepta la hipótesis nula, es decir, los errores siguen una distribución normal.

La prueba de White empleada para probar la existencia de homocedasticidad o heterocedasticidad de las varianzas de los errores, basada en un análisis de regresión auxiliar, se realizó tomando el cuadrado de los errores del modelo original, como variable dependiente y como variable independiente, la variable (longitud de la nervadura central del lóbulo izquierdo, contiguo al adyacente al lóbulo medio (NLICALM = X) y sus valores al cuadrado.

El modelo de regresión auxiliar obtenido fue:

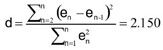
El coeficiente de determinación ajustado de este modelo es el siguiente: R² = 0,0245. Ahora, como nR² = 0,735, es superior a 0,05, estadísticamente se concluye que no hay heterocedasticidad en los errores, por lo tanto, la variación en torno a la recta de regresión es constante para todos los valores de X, sin importar que el valor que toma sea alto o bajo, de todas formas, la variación se supone es la misma.

En la prueba de aleatoriedad (Rachas), se quiso probar si los errores son o no aleatorios.

Ahora bien, como R=19, T1=16 y T2=14, donde R=Número de rachas, T1=Número de errores positivos y T2=Número de errores negativos; se tiene que R I, siendo I=(10-22) el intervalo que contiene a los valores críticos de las rachas al nivel de significancia del 0,05, por consiguiente, los errores corresponden a un arreglo aleatorio, o bien, los errores no están autocorrelacionados, es decir, son independientes, por lo que se determina, que las muestras tomadas para la estimación del modelo son aleatorias y las sucesivas observaciones son independientes.

CONCLUSIONES

El área foliar (AF) de papaya está relacionada linealmente con la longitud de la nervadura central del lóbulo izquierdo, contiguo al adyacente al lóbulo medio.

El modelo lineal simple seleccionado mostró mayor precisión para estimar el área foliar de papaya cultivar Maradol roja y cumple con los supuestos de normalidad, homogeneidad de varianzas e independencia de los errores.

BIBLIOGRAFÍA

AGRONET, 2008. Área cosechada, producción y rendimiento de papaya, 1992-2006. Ministerio de Agricultura y Desarrollo Rural. Disponible desde Internet en: http://www.agronet.gov.co/www/htm3b/repparam.asp. (con acceso 15/03/08).

ALLEN, R.G.; SMITH, M.; PEREIRA, L.S.; PRUIT, W.O. 1997. Proponed revision to the FAO: procedure for estimating crop water requeriments. Acta Horticulturae (ISHS). 449:17-34.

ANUARIO ESTADÍSTICO DE VERACRUZ. 2001. Producción Nacional, Precios y Márgenes de Comercialización de papaya. http://www.sefiplan.gob.mx (con acceso 05/08/08).

ARJONA, H. 2003. Estimación del área foliar de cebolla de bulbo (Allium cepa LYellow Granex F1)mediante la aplicación de tres modelos estadísticos. Revista Comalfi (Colombia). 30(1):28-36.

BIDWELL, R.G.S. 1984. Fisiología Vegetal, Introducción y Generalidades. AGT. Editorial, p.286-315.

BLANCO, F.F.; FOLEGATTI, M.V. 2003. A new method for estimating the leaf area index of cucumber and tomato plants. Hort. Brás. 21(4):666-669.

CAMPOSTRINI, E.; YAMANISHI, O.K. 2001. Estimativa da área foliar do mamoeiro utilizando o comprimento da nervadura central. Scientia Agrícola (Brasil). 58(1):39-42.

CHIRINOS, D.; CHIRUNOS-TORRES, J.; GERAUD-POUEY,F.; FERNÁNDEZ, R., MÁRMOL, L.; CHIRINOS-TORRES, D. 1997. Modelos para estimar el área foliar de melón híbrido Durango. Facultad de Agronomía. Revista la LUZ (Venezuela). 14:163-171.

COSTA, M.C. 1999. Efeitos de diferentes lâminas de água com dois níveis de salinidade na cultura do meloeiro. Tese doutorado, Universidade Estadual de Sao Paulo UNESP Botucatu Brasil. 115p.

ELSER, E.A.; JUBB, G.L. Jr. 1988. Leaf area estimation of concord grape leaves from simple linear measurements. Am. J. Enol. and Vitic. 39(1):95-97.

ESPITIA, M.; MONTOYA, R.; ROBLES, J.; BARBOSA, C.; VERGARA, C. 2006. Modelo estadístico para estimación de área foliar em Stevia rebaudiana. Bertoni em el Sinú medio. Rev. Temas Agrarios (Colombia). 11(2):45-52.

GALVANI, E.; ESCOBEDO, J.F.; CUNHA, A.R; KLOSOWSKI, E.S. 2000. Estimativa do índice de área foliar e da produtividade de pepino em meio protegido - cultivo de inverno e de verão. Rev. Bras. de Engenharia Agrícola e Ambiental.4:8-13.

GAMIELY., S.; RANDEL, W.M.; MILLAS, H.A.; SMITLE, D.A. 1991. A Rapid and Nondestructive Method for Estimating Leaf Area of Onions. HortScience (USA). 26(2):206.

GUJARATI, D. 1997. Econometría. 3ª ed. Editorial Mc Graw-Hill. p.344-391.

GUO, D.P.; SUN, Y.Z. 2001. Estimation of leaf area of stem lettuce (Lactuca sativa var angustana) from linear measurements. Indian J. Agr. Scienc. 71(7):483-486.

HIDALGO, M.; TAPIA, A.; RODRÍGUEZ, W.; SERRANO, E. 2006. Efecto de la sigatoka negra (Mycosphaerella fijiensis) sobre la fotosíntesis y transpiración foliar del banano Musa AAA cv. Valery. Agronomía Costarricense. 30(1):35-41.

KINGSTON, C.M.; VAN EPENHUIJSEN, C.W. 1989. Influence of leaf area on fruit development and quality of Italia glasshouse table grapes. Am. J. Enol. and Vitic. 40 (2):130-134.

MANIVEL, L.; WEAVER, R.J. 1974. Biometric correlations between leaf area and length measurements of ‘Grenache' grape leaves. HortScience. 9(1):27-28.

MONTEITH, J.L. 1965. Light Distribution and Photosynthesis in Field Crops. Annals of Botany (Inglaterra). 29(113):17-37.

MONTGOMERY, D.C.; RUNGER, G.C. 1996. Probabilidad y Estadística aplicadas a la ingeniería. McGraw-Hill Interamericana Editores, S.A., 895p.

MONTOYA, R.; HERNÁNDEZ, M.; CLAVIJO. J. 1991. Determinación de modelos matemáticos para medición de área fotosintética y peso seco en pitaya. Revista Comalfi. 27(2):31-38.

PALENCIA, G.; MERCADO, T.; COMBATT, E. 2006. Estudio agrometeorológico del Departamento de Córdoba. Facultad de Ciencias Agrícolas, Universidad de Córdoba. Gráficas del Caribe. 126p.

PIRE, R.; VALENZUELA, I. 1995. Estimación del área foliar en Vitis vinifera L. “French Colombard” a partir de mediciones lineales en las hojas. Agronomía Tropical (Venezuela). 45(1):143-154.

RAWLINGS, J.; PANTILA, S.; DICKEY, D. 2001.Applied Regresión Análisis, 2nd ed. Edit. Springer. p.204-459.

RIBAS, F.; CABELLO, M.; MORENO, M.; MORENO, A.; LÓPEZ-BELLIDO, L. 2000. Respuesta fisiológica de un cultivo de melón (Cucumis melo L.) a distintas dosis de riego. Invest. Agr. Prod. Prot. Veg. 15(3):196-210.

SAS INSTITUTE INC. 2007. SAS/STAT guide for personal computers version 9.1 Edition. Cary, NC: SAS INSTITUTE Inc. 378p.

SEPASKHAH, A.R. 1977. Estimation of individual and total leaf areas of safflowers. Agronomy Journal (USA). 69(5):783-785.

SINCLAIR, T.R.; HORIE, T. 1989. Leaf nitrogen photosynthesis and crop radiation use efficiency a review. Crop Science (USA). 29(1):90-98.

SQUIRE, G.R. 1990. The physiology of tropical crop production. Wallingford, England. C.A.B. International. 236p.

TERUEL, D.A. 1995. Modelagem do índice de área foliar de cana açúcar em diferentes regimes hídricos. Tese mestrado. Escola Superior de Agricultura, ESALQ, Piracicaba, S.P. Brasil. 93p.

THORNLEY, J.H.M. 1976. Mathematical models in plant and crop physiology. Academic Press, London, New York. 315p.

WALPOLE, M. 1995. Probabilidad y Estadística. 4ª Ed. Edit. McGraw-Hill. p.440-443.

Recibido: Abril 24 de 2008; Aceptado: Febrero 16 de 2009