CIENCIAS EXACTAS Y NATURALES - Artículo Científico

ANÁLISIS A LOS DISEÑOS DE LOS SOMBREROS DE IRACA ELABORADOS EN COLÓN - GÉNOVA, NARIÑO

ANALYSIS OF THE DESIGNS OF IRACA HATS MADE IN COLÓN - GENOVA, NARIÑO

William Enríquez Ortega¹, Brayan Andrés Millán², Armando Aroca Araújo³

¹Licenciado en Educación Básica con énfasis en Matemáticas. Profesor del Colegio Liceo Bella Suiza, matematicas20102011@hotmail.com.

² Licenciado Educación Básica con énfasis en Matemáticas, brayanmillan@hotmail.com.

³ Licenciado en Matemáticas y física. Magíster en Educación Matemática. Profesor Asistente de la Universidad del Valle, trabajosdegrado2010@gmail.com, aroca@etnomatematica.org

Rev. U.D.C.A Act. & Div. Cient. 15(1): 227 - 237, 2012

RESUMEN

Este documento presenta un análisis de los entrecruces que se usan en la configuración de los nueve estilos tejidos en sombreros de paja, producidos por la comunidad de Colón, Génova, Nariño, Colombia. Estos sombreros, se conocen bajo los nombres de Común, Pintao, Gallineto-Granizo, Fino, Cuadros, Calado o Huecos, Costeño o Vueltiao, Bandera y Ojo de Perdiz. La interpretación del pensamiento geométrico que se emplea para su diseño tuvo como referencia, entre otros autores, metodologías propuestas por Gerdes (1999) y Aroca (2009), que han sido aplicadas en el continente Africano y en Suramérica. Además, se estableció la existencia de una lógica de construcción, basada en estrategias de conteo y de organización que se evidencian en el entrecruce de las iracas o chullas. Se evidenció una evolución por medio de la aparición de nuevas técnicas, que implican modificaciones en el tejido básico conllevando a cambios en la lógica de construcción y como consecuencia, se generan nuevos diseños, que buscan responder a las necesidades de la sociedad actual. Los artesanos abordan la simetría en sus diseños, aplicando complejos procesos de estimación y de conteo, que se tratarán de mostrar. Las figuras simétricas corresponden a triángulos, cuadriláteros y hexágonos, que se organizan en franjas, que cumplen con propiedades de congruencia, de semejanza y de paralelismo, siendo éste un lenguaje de interpretación de los investigadores, que se valida en el momento de mostrar los resultados a comunidades académicas.

Palabras clave: Etnomatemáticas, educación matemática, esquema de tejido, sombreros de paja.

SUMMARY

This document presents an analysis of the interlaces used in the configuration of nine straw hat styles produced by the Colón - Génova community, Nariño, Colombia. These hats are known under the names of Común, Pintao, Gallineto- Granizo, Fino, Cuadros, Calado or Huecos, Costeño or Vueltiao, Bandera and Bird's-Eye. The interpretation of the geometric thought employed in the design of these hats had like reference, between other authors, the methodologies proposed by Gerdes (1999) and Aroca (2009), that have been applied in the African continent and in South America. Besides, the existence of a logic of the construction became established, based in count strategies and organization that become evident in the crossed of the iracas or chullas. The evolution techniques were evidenced, which imply modifications in the basic fabric bearing to changes in the logic of the construction, resulting in the generation of new designs that search to fulfill to the needs of the present-day society. Craftsmen discuss the symmetry in their designs applying complex processes of estimate and count, which are tried to show. The symmetric figures correspond to triangles, quadrilateral and hexagons organized in stripes that fulfill properties of congruence, similarity and parallelism, being this a language of the researchers interpretation validated upon showing the results to academic communities.

Key words: Etno-mathematics, mathematics education, web sheme, straw hats.

INTRODUCCIÓN

En este artículo, se presentan las estrategias de conteo, de medición y de diseño que emplean los artesanos del municipio de Colon-Génova, Nariño, en la elaboración de los sombreros de iraca. Dicho conocimiento cultural, se comunica de forma oral y experimental y por años ha sido el sustento económico de la población menos favorecida del municipio. En el tejido de estas artesanías, se evidencia la producción de pensamiento matemático de forma intencionada, o sea, que los artesanos reconocen que están haciendo matemáticas, lo cual, a veces, no se evidencia en otros grupos culturales o sociales. Se manifiesta en estrategias de conteo, de medición, de organización, en la aplicación de secuencias lógicas y la simetría.

Para la interpretación de los diseños y, en particular, su lógica de construcción fue necesario emplear el lenguaje matemático y geométrico que implica el uso de algoritmos. Se entiende por lógica de construcción como el conjunto de procesos de pensamiento, de normas, de medidas, de entrecruces y de regularidades en los diseños, que permiten ejecutar el tejido de los sombreros de iraca, siguiendo los parámetros establecidos por el grupo artesanal. En ningún momento se busca validar las matemáticas de los artesanos, a través de las matemáticas escolares, solo que, por medio de ellas, también se pueden interpretar otras formas de pensamiento matemático o geométrico, tal como lo propuso Aroca (2009), en el análisis de los diseños hechos por las indígenas arhuacas, en 16 figuras tradicionales, que tejen en sus mochilas.

Según varios de los artesanos, sobrevivir de la elaboración de sombreros implica un gran sacrificio y un sinnúmero de dificultades económicas. Según estadísticas del DANE, citadas en el Sitio Oficial del municipio de Colón-Génova, el 65,7% de la población presenta un índice de necesidades básicas y el 31,7% vive en miseria absoluta, la mayoría en el sector rural. Solo en palabras de una artesana, se puede entender la magnitud de la situación: "heredarle a mis hijas el arte de tejer sombreros sería pedirles que vivieran en la miseria y pobreza como nos tocó a nosotros...".

En este marco deplorable, se producen dos fenómenos en la práctica del tejido de sombreros. Primero, una subvaloración económica externa por parte de los individuos que los comercializan; tal vez en la conformación de políticas cooperativas se enfrentarían a esta explotación y, segunda, una subvaloración interna que muestra la actividad como la última alternativa a la que nadie desea llegar. Es por ello, que uno de los impactos que se buscan con el análisis, que no puede ser meramente matemático, es darle un valor agregado de reconocimiento y de respeto a esta actividad etnomatemática. Otro de los propósitos que se tiene es llevar la discusión y la exploración de estas prácticas y saberes artesanales a las aulas de clases del municipio, tal como lo propone Gerdes (1999), quien presenta algunas situaciones que involucran diseños en sombreros, crea actividades que involucran el tejido, estudia los diseños, genera nuevos diseños y aplica técnicas en situaciones matemáticas. Relacionado a esto, Knijnik (2010) propone que es necesario relacionar la educación matemática y la etnomatemática con la formación cultural, que los estudiantes traen consigo. Con esta intención, se presenta un beneficio añadido a los profesores, en cuanto a la construcción de situaciones a-didácticas, como lo plantea Brousseau, (2007) (D'Ambrosio, 2011).

En un barrido por algunas concepciones sobre la etnomatemática, encontramos a D'Ambrosio (1985a), en el sentido que las matemáticas se producen en los grupos culturales diferenciados y modelan sus propios patrones de comportamiento, códigos, símbolos, modos de razonamiento, maneras de medir, de clasificar y, en general, de matematizar. Blanco (2006) establece las limitaciones que tienen las matemáticas y la antropología para que cada una de ellas, por separado y pueda explicar las prácticas de grupos sociales bien diferenciados. Barton (1996) indica que la etnomatemática determina cómo los grupos culturales entienden, articulan y usan los conceptos y las prácticas en sus relaciones con sus entornos y que se describen como matemáticos. Estas apreciaciones implican cuál podría ser el tratamiento de las formas de pensar, formas de hacer y formas de decir, cuando se pretendan incorporar al currículo. En la actualidad, la naturaleza genérica de la educación se ha convertido en un problema, como lo plantea D'Ambrosio (1985b), pues crea una barrera para acceder a la sociedad. La investigación en etnomatemáticas brinda una luz al emplear el estudio de la diversidad de prácticas y de saberes, puesto que enseñar matemáticas, desde esta perspectiva, implica tener en cuenta la cultura de los estudiantes. En palabras de D'Ambrosio (1988; 1993), la Etnomatemática proporciona al educador saber quiénes son sus alumnos, lo que hacen y cuál es su mundo social. Para que esto ocurra, él debe ser un investigador, alterando su rutina del salón de clases.

MATERIALES Y MÉTODOS

La investigación, se realizó en dos fases. En la primera, se describieron las técnicas del tejido de cada estilo. Para la recolección de información, se realizaron entrevistas semi estructuradas o abiertas, a diez artesanos del municipio; se usaron dispositivos de audio, fotos y videos, para el posterior análisis (Deslauriers, 2005); además, se hicieron necesarios la implementación de protocolos de observación paralelos a las narraciones y explicaciones de los artesanos. Las primeras entrevistas se realizaron en Colón Génova, en uno de los centros de acopio, donde concurren los artesanos; de la población encuestada, se eligieron aquellos que contaban con mayor experiencia y que conocían la mayoría de los estilos. Adicional al tejido, también se estudió la incidencia de los cultivadores de la planta de iraca o "paja toquilla", Carludovica palmata; para esto, las entrevistas se realizaron en el municipio de Florencia - Cauca, siguiendo las mismas estrategias con los artesanos; de la misma forma, se indagó a los encargados del proceso de acabado. Esta primera fase de la investigación tomó como soporte a Morse et al. (2007), quien en los métodos de investigación cualitativos, describe el análisis etnográfico, como la búsqueda de patrones en los datos y en las ideas, que ayuden a explicar la existencia de éstos.

En la segunda fase, se analizó la simetría en cada uno de los nueve estilos de sombreros, que se muestran en la figura 1. En el análisis, se mencionan las principales características, tomando como referencia las narraciones de los artesanos y las observaciones registradas de su práctica; luego, se efectúa la deconstrucción geométrica de cada diseño. Al determinar la unidad mínima que lo genera o patrón figural, se reconstruyó la figura usando las indicaciones y las propiedades que los artesanos ejecutan; en esta fase, se empleó el programa de geometría dinámica GeoGebra. Se usó la herramienta "intercalar imagen" para insertar una imagen de cada estilo de sombrero, de esta forma, al utilizar rectas paralelas, perpendiculares y también polígonos, encima de la figura, se determinaron las franjas y los patrones que los artesanos usan, lo que conllevó a obtener una representación bidimensional del diseño.

Además de la deconstrucción geométrica basada en Aroca (2009), el análisis también tuvo en cuenta a Gerdes (1988, 1989, 1991, 1994, 1999), donde se analizan algunos diseños relacionados con nuestro objeto de estudio. Por ejemplo, se tomó como ejemplo, los análisis realizados por él a algunos cestos elaborados por indígenas de Brasil y los Bora, del Perú. En el texto, se especifican conjeturas de orden geométrico y aritmético, que se pueden notar en las figuras.

RESULTADOS Y DISCUSIÓN

Para decorar los sombreros, los artesanos utilizan iracas de colores, ya que el color juega un papel destacado a la hora de configurar el patrón figural. No se podría tejer un diseño tradicional si no se incluyen, al menos, dos colores diferentes. No hay desarrollo de pensamiento geométrico significativo si no hay un juego de colores. Las iracas se pintan por separado antes de tejer, utilizando hojas de nogal medicinal, Juglans regia o anilinas de colores. Para los artesanos, la implementación del color brinda la posibilidad de configurar sus diseños. Según ellos, en un principio, los sombreros solo eran blancos; a partir de éstos, se aprendieron o se desarrollaron técnicas que les permitían hacer más vistosos sus sombreros y, de la misma forma, obtener un mejor precio en el mercado. El empleo de color en el tejido creó la diversidad de diseños, estimulando en los artesanos la creatividad y la imaginación.

Tejido básico del sombrero de iraca: Las partes fundamentales del sombrero de iraca, las cuales, se tejen en un orden específico, son la plancha, la copay la falda, y se describen de forma general a continuación. La plancha es un círculo que oscila entre 10cm y 15cm de diámetro, dependiendo de la talla y del género: Se identifican dos partes adicionales, que son fundamentales en el tejido de un sombrero: el empiezo y el crecío; el primero es la parte inicial del sombrero, en donde se teje en cuatro pasos o cadejos, que forman un óvalo y alrededor de éste se tejerá todo el sombrero y en el crecío, se adicionan o se pegan las iracas necesarias para darle forma al sombrero. Un sombrero debe tener como mínimo tres crecidos, siendo necesario uno en cada parte del sombrero. La copa es un cilindro que tiene como base la plancha, su longitud es de aproximadamente 10cm y su diámetro corresponde a las dimensiones de la plancha. La falda o ala, se teje de acuerdo al modelo, esta puede variar entre 15cm a 20cm. Para diferenciar los modelos de hombres y de mujeres, se dobla la falda hacia arriba para ellos y hacia abajo para ellas.

La construcción de un sombrero de iraca implica los siguientes pasos: Paso 1: Conteo. En esta etapa, se establece el número de iracas, con las cuales, se iniciará la construcción del sombrero; las fibras se cuentan en pares, cinco es el menor número con las que se puede construir un sombrero y el máximo es 15 pares (Figura 2). Paso 2: Amarrado. Se utiliza un trozo del tallo de la iraca partido por la mitad para amarrar los pares de fibras deseados. Las iracas se pueden atar en la mitad o en uno de sus extremos, dependiendo del tipo de sombrero que se quiera tejer. Para los de tamaño medio, se atan a la mitad y para obtener un sombrero para adulto, en uno de sus extremos; este paso tiene como objetivo brindar estabilidad y soporte al empiezo (Figura 2). Paso 3: Tejido de los cadejos. Se teje el empiezo del sombrero, el cual, se compone de cuatro cadejos. Para iniciar, se pega la primera iraca, levantando un par por medio, por ejemplo, para un sombrero de cinco pares, se levantarán el primer, tercer y quinto par, luego, se baja una iraca de cada par; para pegar la iraca siguiente, se deja la última iraca del lado izquierdo atrás, no se sube y, nuevamente, se levanta un par por medio. El proceso se repite sucesivamente hasta que se hayan dejado atrás las diez iracas, con las que se inicia; en este punto se habrán pegado cinco pares más. A esta primera parte, se le denomina cadejo; luego, se ata y se procede a tejer dos cadejos más, para los cuales, se emplea el mismo proceso; en estos, se agregan cinco pares más en cada uno. En el cuarto cadejo, el que cierra el empiezo, se teje usando las iracas del primero, de esta forma se obtiene una forma esférica, que es la parte inicial, sobre el cual, se tejerá el resto del sombrero. Un mejor ilustración se puede ver la Figura 3-a.

La vuelta o chulla, se teje alrededor del sombrero y puede iniciar con cualquier iraca y en cualquier parte del sombrero; después de establecer el punto de partida, se elije una iraca de trama, se deja abajo el par contiguo a ésta y se sube el siguiente, quedando un par arriba y uno abajo; luego, se pasa la trama y se baja el par que se encontraba arriba, se deja la iraca de atrás y la de adelante se sube con la iraca siguiente, se forman nuevamente dos pares en cada posición; esto se repite para cada iraca de trama, hasta terminar una vuelta de 360°.

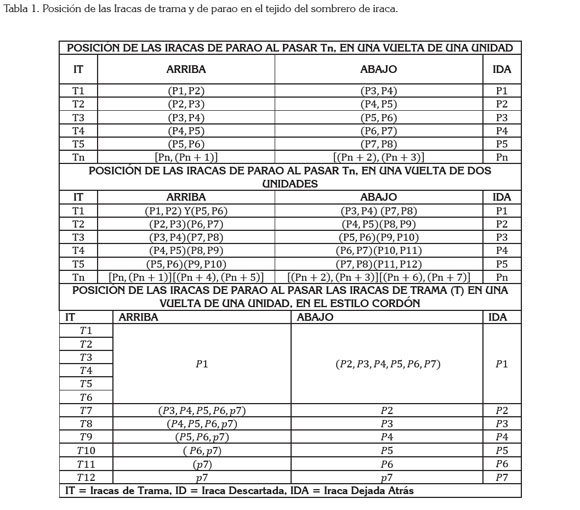
Análisis a los nueve diseños hechos en los sombreros: Se debe precisar que cada uno de los nueve diseños se tejen usando la misma técnica para el sombrero común y, solo en aquellos que presentan huecos o triángulos, Calado o Huecos, Costeño o Vueltiao y Ojo de Perdiz, existen variaciones en el tejido; la tabla 1 muestra este proceso de construcción. Los sombreros que solo presentan diseños realizados con iracas de color, Común, Pintao, Gallineto-Granizo, Cuadros y Bandera, se tejen usando técnicas de conteo al momento de intercalar las iracas de trama y de parao en cualquiera de los tres crecíos y, el sombrero fino puede presentar cualquiera de los ocho estilos anteriores, pero su construcción implica condiciones especiales.

Sombrero Común: Es el sombrero de un solo color y no presenta diseños; este tipo se produce en mayor cantidad, puesto que todos lo saben tejer y los principiantes aprenden primero este estilo. El sombrero se teje de izquierda a derecha, el tamaño de la vuelta depende de la habilidad del artesano y determina también la cantidad de vueltas que se deberá dar para terminar un sombrero, es decir, que entre mayor sea el número de chullas en cada vuelta será menor la cantidad de vueltas para terminar el sombrero.

Descripción de una vuelta o chulla: Los artesanos solo deben organizar las iracas de trama y de parao, para no cometer errores o fallos, los cuales, se producen cuando se intercambia de posición una iraca de trama con una de parao, produciendo un hueco en el sombrero. Otro error típico es crear una vueltaciega y esto ocurre cuando se genera una vuelta que no cierra y continúan un nivel por arriba, sin encontrar un final. Por lo general, cuando una de las dos situaciones anteriores sucede, los artesanos desbaratan o desarman el tejido hasta encontrar el fallo.

En la Figura 3-b, se muestra la organización de las iracas de trama y de parao empleadas en el tejido de una vuelta de dos unidades; en ésta, las iracas representadas con las Pi, P1, P2, P3, P4, P5 y P6, corresponden a las iracas de parao, que se deben intercalar para tejer dicha vuelta, y las iracas Ti, siendo ellas las T1, T2, y T3, corresponden a las iracas de trama, que se entrecruzan. La cantidad de iracas de parao que se emplean depende del número de unidades que se deseen tejer de forma simultánea, mientras que las iracas de trama, se emplean una cada vez. El número de unidades que se tejen, se puede evidenciar en la cantidad de pares de iracas que se levantan; por ejemplo, en la Figura 3-b, se encuentran en la parte de arriba los pares de iracas conformadas por P1, P2 y P5, P6, respectivamente, por lo tanto, se tejerán dos unidades. Si la vuelta fuese de una chulla, se encontraría levantado el par P1 y P2, mientas que para cualquiera de los dos casos anteriores, solo se pasaría únicamente la iraca de trama T1. Al pasar T1 se baja el par P1 y P2, dejando atrás a P1 y subiendo nuevamente a P2 con P3, quedando arriba el par conformado por P2 y P3; luego, se baja el par P5 y P6, se deja atrás a P5 y se sube P6 con P7; después de esto, se toma la iraca siguiente P9, quedando entonces los pares P2, P3 y P6, P7, arriba y los pares P4, P5 y P8, P9, abajo. Tomando como referencia el proceso descrito anteriormente, al pasar a T2 se descarta a P2 y los pares quedarán ordenados de la siguiente manera: P3, P4 y P7, P8, arriba; P5, P6 y P9, P10, abajo. La tabla 1 ilustra el proceso para Pn en el tejido de una vuelta de una y dos unidades. En el entrecruce de la iraca de parao que se deja atrás, P1 y la de trama que se pasa T1, se genera una parte expuesta, correspondiente a las dimensiones de la fibra de iraca; esta parte se presenta en dos posiciones en el tejido y así generan la superficie del sombrero.

Formas: La superficie del sombrero, se compone de pequeños cuadriláteros de diferentes dimensiones, que se originan por el entrecruce, a los cuales, los artesanos los denominan cuadros o cuadritos. El largo y ancho de cada uno de estos depende del diámetro de la iraca, por esta razón, sus dimensiones pueden variar, aunque ellas tienden a ser similares. Cada cuadrilátero comparte sus lados con los siguientes, recubriendo totalmente el plano del sombrero. Los artesanos conciben la superficie ideal del sombrero, totalmente recubierta, sin errores o fallos y, para esto, efectúan el entrecruce de iracas, procurando que quede el menor espacio posible entre las fibras y, bajo este estricto cuidado, el patrón figural corresponde a la unidad mínima, que compone la superficie del sombrero, un cuadrilátero.

Sombreros que emplean únicamente el tejido básico: Sombrero Común, Pintao, Gallineto-Granizo, Cuadros y Bandera: El patrón figural de estos cinco estilos corresponde a un cuadrilátero formado por la parte expuesta de una iraca; aquellos que presentan diseños producidos por iracas de color, se tejen intercalando franjas de distintos números de iracas, entre éstos, tenemos desde las más delgadas compuestas por una fibra en el sombrero Gallineto o Granizo y Pintao, hasta las más pronunciadas, pertinentes al estilo Bandera, cuya superficie se compone de tres franjas únicamente. Los diseños presentes en los estilos anteriores, se producen en el lenguaje de las matemáticas escolares, por las transformaciones de isometría correspondientes a traslación, rotación y reflexión puntual.

Sombreros que presentan variaciones en el tejido: Costeño o Vueltiao, Ojo de Perdiz, Calado o Huecos: Los estilos Costeño o Vueltiao y Ojo de Perdiz, se tejen por medio de una técnica denominada cordón; en ésta, se entrecruzan grupos de iracas de trama y de parao de forma simultánea. El patrón figural, además de presentar los cuadriláteros habituales formados en el tejido básico, está compuesto por triángulos escalenos y cuadriláteros de diferentes tamaños, que se presentan en dos o más posiciones. El estilo Calado o Huecos muestra características únicas; se teje a través de la técnica denominada huecos, la cual, intercambia dos o más iracas de posición; el patrón figural corresponde a un hexágono.

La excepción a los anteriores sombreros es el Sombrero Fino, que puede presentar cualquier estilo y es el más escaso de todos, debido a que pocos artesanos se dedican a su construcción por las exigencias en cuanto a la estética y a la precisión del diseño; se teje con iracas especiales, cuyo diámetro asemeja a un hilo de cocer; puede presentar cualquiera de los ocho estilos o combinar varios, por lo cual, puede presentar las características geométricas descritas.

Para identificar algunos campos de aplicación, en los que se puedan vincular los conceptos y las prácticas culturales de los artesanos, dentro del currículo matemático de los colegios del municipio de Colón Génova, se tomarán como referencia los componentes simbólico y cultural, propuestos por Bishop (1999), en el proceso de enculturación del currículo.

Mosaicos presentes en los nueve modelos tejidos en los sombreros de iraca, posibilidades en la educación matemática: Los docentes y los estudiantes pueden emplear los mosaicos para el tema de teselaciones e implementarlos, en vez del desarrollo de las clases habituales, como sugiere Brousseau (2007), en el desarrollo de situaciones, a manera de proyectos, que involucren este tipo de representaciones. Se usarían, preferiblemente, los sombreros en físico, los estudiantes podrían llevar a sus familiares y los sombreros que hacen. Sería una especie de clase comunitaria. Los estudiantes podrían realizar mediciones, comparaciones, representaciones e, incluso, relacionar los diseños presentes en las franjas, a través de movimientos geométricos. Si se quiere avanzar al campo de las representaciones bidimensionales, se sugiere emplear los programas de geometría dinámica, para establecer relaciones entre los diseños, a partir de las imágenes, descargando software libre, como el Geogebra o Regla y Compás; por ejemplo, se podría proponer a los estudiantes que realicen la representación bidimensional del estilo calado: a partir del recorte de una imagen determinen las relaciones geométricas existentes entre los hexágonos que conforman el diseño, usando el programa de geometría dinámica GeoGebra y, luego, reflexionar sobre los procesos de conteo, de organización y de estimación empleados por los artesanos, para producir las relaciones de igualdad, de congruencia, en las franjas que contienen los diseños, para esto deberán consultar a los artesanos.

Una actividad ideal consistiría en desarrollar un proyecto de aula, como propone Bishop (1999), donde los estudiantes aprendan a construir los diseños y, a partir de éstos, estudien las relaciones geométricas producidas, reflexionando sobre la lógica de construcción de los sombreros; por ejemplo, los artesanos consideran que dos figuras son iguales o congruentes cuando se componen de la misma cantidad de fibras de iraca. Estos criterios, se pueden incorporar como pruebas visuales, que permitan a los estudiantes relacionar figuras, de acuerdo a las relaciones comunes presentes en cada una de ellas y, posteriormente, generalizarse a demostraciones más estructuradas, soportadas en axiomas y en teoremas, tales como los criterios que emplean las relaciones de lados y de ángulos.

Los artesanos cuentan, también, con criterios de paralelismo, pues dos iracas de trama o dos de parao son paralelas, por describir trayectorias en el sombrero que no se cruzan. Todas las iracas de trama o de parao son paralelas entre sí, exceptuando los estilos de sombrero que las entrecruzan, intencionalmente, para producir algún efecto, como por ejemplo, en el estilo calado. Al igual que los criterios de congruencia, esta noción de paralelismo desarrollada y aplicada de forma cultural, puede ser usada como herramienta de visualización: los estudiantes pueden comprobar el paralelismo entre dos iracas en una imagen o un sombrero, para luego establecer similitudes y diferencias entre las concepciones de los artesanos y las teorías establecidas. Además, la forma de los sobreros, permiten explorar otras nociones, no euclidianas, como las de recta y plano.

Por ejemplo, para lograr la simetría entre los triángulos blanco - blanco, negro - negro y negro - blanco, como lo muestra la figura 4, los artesanos emplean estrategias de conteo, procurando que cada triangulo de cada color tenga la misma cantidad de iracas, es decir, que se pretende una simetría aritmética, en la cantidad de iracas que contiene cada triangulo, lo que produce a su vez una franja de triángulos "iguales"; luego, la igualdad entre los triángulos no solo es importante para la estética, sino que también es fundamental, porque triángulos desiguales deforman el sombrero y no hacen posible su construcción; posteriormente, desde una perspectiva geométrica y empleando las nuevas tecnologías, se puede visualizar que entre un triángulo blanco y el negro se puede establecer una relación de igualdad entre sus áreas. Las franjas que rodean el sombrero (Figura 4) son paralelas entre sí y el segmento mayor de los triángulos es igual, por contener la misma cantidad de iracas. Luego, como la distancia entre dos paralelas es constante, los dos triángulos tienen igual base y altura. Como consecuencia, sus áreas son semejantes e, inclusive, iguales. Con esta estrategia es posible estudiar las relaciones geométricas existentes entre todos los diseños presentes, en los nueve estilos de sombrero.

Las investigaciones que conduzcan a que los estudiantes indaguen las prácticas y los saberes con la comunidad y, potencialmente, con sus familiares, puede implicar el reconocimiento de los saberes que entrañan sus prácticas en los diferentes campos y, a partir de aquí, didácticamente hablando, acceder a los saberes formales o escolarizados. Para lograr dicha articulación, se hace necesario cambiar las actividades cotidianas de clase por ambientes dinámicos, que permitan la participación activa de los estudiantes, donde ellos asumen el papel de agentes activos. Es por medio de esta articulación que puede ser posible mediar en el conflicto currículo y cultura. Una mirada al currículo correspondiente al área de educación matemática, en las dos únicas instituciones educativas de Colón-Génova: Leopoldo López Álvarez y Divino Niño, deja vislumbrar la posibilidad de diseñar proyectos de aula en algunos temas, como teselaciones, movimientos geométricos, unidades de medida, entre otros; sin embargo, entre las resistencias u obstáculos que se presentan y, en especial las derivadas por las creencias de los profesores, no es posible pensar que la propuesta encontrará un camino llenos de flores y aplausos. El cambio real está en trasformar el currículo en un proyecto curricular, que se base en la investigación, que ayude a los estudiantes a construir su propio conocimiento, a través de la experiencia y que, además, les permita resolver e interactuar con situaciones reales de su comunidad. Corresponde a un estilo similar al que propone el Proyecto Ondas de Colciencias, en todo el territorio nacional.

Por último, el tejido de los sombreros de iraca, en su proceso evolutivo ha desarrollado, aplicado y homogenizado prácticas matemáticas, que se manifiestan en la simetría de los diseños (cuadriláteros, triángulos y hexágonos), presentes en los nueve estilos de sombrero. En este sentido, es prudente articular los saberes escolares con aquellos que son propios de cada grupo cultural. Una alternativa es el desarrollo de proyectos de aula, en los cuales, estudiantes, profesores, padres de familia o artesanos interactúen como investigadores de su propio medio, potencializando el acceso a los saberes "universales" o escolarizados de la educación matemática, en lo posible basado en la educación multicultural, que proponen Orey & Rosa (2004), como un campo de estudio diseñado para aumentar la equidad educativa para todos los estudiantes.

Conflicto de intereses: No se presenta el nombre de ningún artesano o artesana para proteger su identidad. El artículo fue preparado y revisado con la participación de los tres autores, quienes declaramos que no existe ningún conflicto de intereses que ponga en riesgo la validez de los resultados presentados. Financiación: La financiación de esta investigación corrió por cuenta de los investigadores.

BIBLIOGRAFÍA

1. AROCA, A. 2009. Geometría en las Mochilas Arhuacas. Por una enseñanza de las matemáticas desde una perspectiva cultural. Ed. Universidad del Valle. (Colombia). 234p.

2. BARTON, B. 1996. Making sense of ethnomathematics: Ethnomathematics is making sense. Rev. Ed. Studies in Math.(Dordrecht).31(1/2):201-233.

3. BISHOP, A. 1999. Enculturación matemática, la educación matemática desde una perspectiva cultural. Ed. Paidós Ibérica S.A. 239p.

4. BLANCO, H. 2006. La etnomatemática en Colombia: un programa en construcción. Rev. Bolema: Bol. Ed. Matemática. 19(26):49-75.

5. BROUSSEAU, G. 2007. Iniciación al estudio de la teoría de las situaciones didácticas. Ed. Editorial Zorzal. (Buenos Aires). 125p.

6. D'AMBROSIO, U. 1985a. Boletines del Grupo de Estudio Internacional de Etnomatemática: ISGEM. Vol.1, No. 1, Compilación Hilbert Blanco Álvarez. Disponible desde internet en http://etnomatematica.org/isgem. php (con acceso el 03/05/2010).

7. D'AMBROSIO, U. 1985b.Socio-Cultural Bases forMathematicsEducation. Edi. UNICAMP. (Brasil). 103p.

8. D'AMBROSIO, U. 1988. Etnomatemática se ensina? Rev. Bolema: Bol. Ed. Matemática. 03(4):43-46.

9. D'AMBROSIO, U. 1993. Etnomatemática: Um Programa. Ethomathematics: A program]. Rev. Ed. Mat. em Ver.1(1):5-11.

10. D'AMBROSIO, U. 2011. Uma Síntese Sociocultural da Historia da Matematica. Edi. PROEM. (Brasil). 96p.

11. DESLAURIERS, J. 2005. Investigación cualitativa. Guía práctica. Ed. Papiro. (Colombia). 142p.

12. GERDES, P. 1988. On culture, geometrical thinking and mathematics education. Rev. Ed. Studies Math. 19:137-162.

13. GERDES, P. 1989. Aritmética e Ornamentação Geométrico: Analise de alguns cestos de índios do Brasil. Rev. Bolema: Bol. Ed. Matemática. 4(1):206- 247.

14. GERDES, P. 1991. On ethnomathematical research and symmetry. Rev. Symmetry: Culture and Science. 8(1):154-170.

15. GERDES, P. 1994. Fivefold Symmetry and (Basket) Weaving in Various Cultures. En: Hargittai, I.(ed). Fivefold Symmetry. (Singapore). p.245-262.

16. GERDES, P. 1999. Geometry from Africa. Mathematical and educational explorations. Ed. Current Printing. (Estados Unidos). 217p.

17. KNIJNIK, G. 2010. Entrelaçamentos e dispersões de enunciados no discurso da educação matemática escolar: umestudo sobre a importância de trazer a "realidade".Rev. Bolema: Bol. Ed. Matemática. 23(37):863-886.

18. MORSE, H.; BOTTORFF, J.; ZIMMERMAN, E. 2007. Asuntos críticos en los métodos de investigación cualitativa. Ed. Universidad de Antioquia (Colombia). 185p.

19. OREY, D.; ROSA, M. 2004. Ethnomathematics and the teaching and learning mathematics from a multicultural perspective. En: Favilli, F. eds. Ethnomathematics and mathematics education. Tipografia Editrice Pisana. (Copenhagen). 156p.

20. Sitio oficial de Colón Génova Nariño. Disponible desde internet en:http://www.colongenova-narino.gov.co/ sitio.shtml?apc=B-xx1&x=2079202#arriba(con acceso el 29/11/2011).

Recibido: Enero 5 de 2012 Aceptado: Marzo 30 de 2012