CIENCIAS DE LA SALUD-Artículo Científico

SIMULACIONES DE CÉLULAS DE CUELLO UTERINO DESDE NORMALIDAD HASTA ATIPIAS ESCAMOSAS DE SIGNIFICADO INDETERMINADO (ASCUS) CON GEOMETRÍA FRACTAL

SIMULATIONS OF CERVICAL CELLS FROM NORMAL TO ATYPICAL SQUAMOUS CELLS OF UNDETERMINED SIGNIFICANCE (ASCUS) WITH FRACTAL GEOMETRY

Javier Rodríguez¹, Signed Prieto², Luis Tabares³, Astrid Rubiano⁴, Ingrid Prieto⁵, Darío Domínguez⁶, Marcela Mejía⁷, Leonardo Ramírez⁸

¹ MD. Director del Grupo Insight. Director de la Línea de Profundización e Internado Especial: Física y Matemáticas Aplicadas a la Medicina, Universidad Militar Nueva Granada - Centro de Investigaciones de la Clínica del Country. Cra 79B No. 51-16sur. Int 5, Apt 102. Bogotá, Colombia. grupoinsight2025@yahoo.es

² Investigadora Grupo Insight. Universidad Militar Nueva Granada - Centro de Investigaciones de la Clínica del Country. Cra 79B No. 51-16sur. Int 5, Apt 102. Bogotá, Colombia. grupoinsight2025@yahoo.es

³ Ingeniero Electrónico. Especialización en telecomunicaciones. Docente Investigador Grupo TIGUM. Universidad Militar Nueva Granada Calle 109 No 5-64, Bogotá, Colombia. luis.tabares@unimilitar.edu.co

⁴ Ingeniera Mecatrónica. Magister Sistemas Automáticos De Producción. Docente de Investigación Grupo TIGUM. Universidad Militar Nueva Granada. Cr. 60 N 79 b- 46 Apto 109, Bogotá-Colombia. astrid.rubiano@unimilitar.edu.co

⁵ Licenciada en Biología. Investigadora Grupo Insight. Universidad Militar Nueva Granada. Cra 79B No. 51-16 sur. Int 5, Apt 102. Bogotá, Colombia. grupoinsight2025@yahoo.es

⁶ Matemático. Magister en Ciencias Económicas. Director Grupo de Investigación FRACUMNG. Universidad Militar Nueva Granada. Cra 53 A No 127-70, Apt 1219. dario.dominguez@unimilitar.edu.co

⁷ Ingeniera Electrónica. Ph.D. Magister en telecomunicaciones. Doctora en Ingeniería y Doctora en Telemática. Investigadora Grupo TIGUM. Universidad Militar Nueva Granada. Calle 120 No 51-91.Bogotá, Colombia. angela.mejia@unimilitar.edu.co

⁸ Ingeniero Electrónico. Ph.D. Magister en Ingeniería de sistemas y Doctorado en Ingeniería en Biomédica. Director Grupo TIGUM. Universidad Militar Nueva Granada. Crr 50 A No 174B-67 Apt 202 Torre 3. leonardo.ramirez@unimilitar.edu.co

Rev. U.D.C.A Act. & Div. Cient. 16(2): 303-311, Julio-Diciembre, 2013

RESUMEN

Los sistemas convencionales de evaluación de la citología cervicouterina presentan problemas de reproducibilidad al basarse en observaciones cualitativas, por ello, se desarrolló una metodología diagnóstica de células cervicales desde geometría fractal. A partir de las dimensiones fractales de objetos definidos en la célula, se han encontrado diferencias entre normalidad y enfermedad; además, se ha mostrado que la clasificación ASCUS (Atipias Escamosas de Significado Indeterminado) podría ser aclarada, al evidenciar su comportamiento matemático similar o bien a normalidad o a enfermedad. También, se desarrolló una generalización de dicha metodología que mostró todos los posibles prototipos, desde normalidad hasta carcinoma. A partir de la generalización desarrollada y partiendo de tres células normales, en este trabajo se realiza una simulación de posibles alteraciones celulares, desde normalidad hasta el estado de ASCUS, cuyos valores matemáticos pueden ser de normalidad o de LEIBG (Lesión Intraepitelial de Bajo Grado). Se simularon tres posibles variaciones geométricas para cada célula en el espacio de Box Counting, se calculó la dimensión fractal para núcleo, citoplasma y totalidad, manteniendo los valores de variabilidad y AMI (Armonía Matemática Intrínseca) celular. Se obtuvieron simulaciones de posibles trayectorias de normalidad a ASCUS, tanto con características de normalidad como con características de LEIBG, con medidas cuantitativas, objetivas y reproducibles. Se evidenció una organización fractal en la arquitectura de las células denominadas ASCUS, que permite el desarrollo de trayectorias acausales de alteración celular, de utilidad en la práctica clínica diaria.

Palabras clave: Dimensión fractal, Cáncer de cuello uterino, Citología, simulación, ASCUS.

SUMMARY

Conventional systems for evaluation of cervical cytology have reproducibility problems in relying on qualitative observations. Thus a methodology was developed to diagnose cervical cells from fractal geometry. From the fractal dimensions of objects defined in the cell, it was found differences between normality and disease. Also has been shown that the classification ASCUS (Atypical Squamous Cells of Undetermined Significance) could be clarified by demonstrating its mathematical behavior similar to normal or disease. Besides, it was developed a generalization of such methodology showing all possible prototypes from normal cells to carcinoma. From the generalization developed and starting with three normal cells, in this work is made a simulation of possible cellular alterations from normality to ASCUS state whose mathematical values can be normal or LSIL (Low-grade Squamous Intraepithelial Lesion). For this, three possible geometric variations for each cell in the space of box counting was simulated, fractal dimension was calculated for nucleus, cytoplasm and whole, maintaining the values of variability and cellular AMI (Intrinsic Mathematical Harmony). Simulations of possible trajectories from normal to ASCUS were obtained, both with normal characteristics or L-SIL characteristics, with quantitative, objective and reproducible measures. It showed a fractal organization of the cell architecture called ASCUS, which allows the development of non-causal trajectories of cellular alteration useful in daily clinical practice.

Key words: Fractal dimension, Cervical Cancer, Cytology, simulation, ASCUS.

INTRODUCCIÓN

Desde la aparición de la geometría fractal con el cuestionamiento de la capacidad de medida de objetos irregulares de la geometría euclidiana (Mandelbrot, 1967), se han planteado diferentes aplicaciones a diversas áreas, como el caso de la medicina. Se ha mostrado, la irregularidad de las estructuras anatómicas y cómo la geometría fractal ha sido de utilidad en la medida de dichas estructuras, que permite desarrollar metodologías apropiadas para caracterizar estados de normalidad o de enfermedad (Goldberger et al. 1990; Goldberger et al. 2002; Kiselev & Hahn, 2003; Cheng & Huang, 2003; Mauroy et al. 2004; Garte, 2004; Bassingthwaighte et al. 1994).

Específicamente, en el área de oncología, la geometría fractal ha mostrado ser de gran utilidad en la descripción de estructuras cancerígenas (Baish & Jain, 2000; Luzi et al. 1999; Sankar & Thomas, 2010), se ha empleado en la medición de mamografías (Stepień & Stepień, 2010), así como en el estudio de la identificación de cáncer primario, en casos de metástasis en huesos (Vasiljevic et al. 2012); sin embargo, se sigue investigando en la aplicabilidad clínica de algunas de estas metodologías (Stehlík et al. 2012; Welter & Rieger, 2010) y, también, se ha mostrado que la medida de dimensiones fractales aisladas puede ser insuficiente en la caracterización matemática para una aplicación clínica efectiva (Goldberger et al. 2002; Rodríguez et al. 2002, 2006,2007, 2012).

En contraposición, el uso de geometría fractal junto con conceptos adecuados para su evaluación, ha permitido el desarrollo de metodologías de evaluación de arterias coronarias en modelos experimentales de restenosis en porcinos (Rodríguez et al. 2002), determinando la totalidad de posibles arterias normales y restenosadas (Rodríguez et al. 2010); también en morfología celular, permitió la determinación objetiva del estado eritrocítico (Correa et al. 2012), mediante la realización de medidas fractales y euclidianas simultáneas.

Por otro lado, estudios realizados muestran que el cáncer de cuello uterino ocupa el segundo puesto en incidencia en el mundo entre los tumores malignos de la mujer, después del cáncer de mama. En el continente americano, el cáncer cervical es el cuarto más frecuente en mujeres, siendo el segundo cáncer más frecuente en las mujeres entre 15 y 44 años (WHO/ICO, 2010). De acuerdo con reportes de la Organización Mundial de la Salud del 2008, esta patología es responsable de 275.000 muertes anuales a nivel mundial y más del 80% de los casos se presentan en países en desarrollo (WHO, 2008a), presentándose 2.000, de éstas, en Colombia, cifra que ubica al país como el cuarto lugar con mayor mortalidad por esta causa en las Américas (WHO, 2008b).

Dado que es una enfermedad con una larga historia natural y que el cérvix es fácilmente accesible, el cáncer de cuello uterino puede ser prevenido mediante el uso sistemático de la citología cérvico vaginal, que permite detectar anomalías previas a la instauración del carcinoma, logrando una tasa de sobrevida de las pacientes a 5 años por encima del 90%, lo que hace de este examen una herramienta fundamental, para la reducción de la mortalidad (Weiderpass & Labrèche, 2012). En la actualidad, la evaluación citológica se basa en parámetros de carácter principalmente cualitativo, lo que dificulta el establecimiento de un único sistema de clasificación de los grados de lesión de la enfermedad.

Actualmente, existen dos sistemas utilizados para reportar las CCV: uno, es de la Sociedad Británica para la Citología Clínica y, el otro, de Estados Unidos (Sistema de Bethesda). La clasificación de Bethesda tiene un uso más amplio, debido a que facilita la comunicación entre el médico y el técnico de laboratorio al proporcionar una terminología uniforme y definida para el establecimiento de los diagnósticos (Dim, 2012). Análisis de la capacidad diagnóstica de estas clasificaciones evidencian que, por lo general, se cuenta con una especificidad entre el 86 y el 100%; sin embargo, la sensibilidad obtenida es altamente variable, oscilando entre el 30 y el 80%. Se ha demostrado, además, que se tiene una menor especificidad para lesiones intraepiteliales de alto grado que para lesiones de bajo grado (Stoler & Schiffman, 2001). Nanda et al. (2000) realizaron una revisión sistemática de este fenómeno encontrando una especificidad promedio del 98% y una sensibilidad promedio de solamente 51%. Además, estudios de las tasas de falsos negativos obtenidos en la citología indican que se presenta un promedio de 35,5% (Spence et al. 2007).

Dentro del estudio de la progresión tumoral existe gran interés por las lesiones pre-malignas del cérvix; se conoce que las lesiones precursoras que aparecen en el cérvix pueden, con el tiempo, transformarse en cáncer invasivo. Así, también es de gran interés la aparición de ASCUS, pues se pueden deber a un proceso benigno o a una lesión de riesgo, ya que el término ASCUS (Lacruz, 2003; Editorial Commite of Acta Cytol, 1993) fue introducido, con el fin de señalar cambios que no pueden ser clasificados de manera inequívoca y que por sus características morfológicas, se pueden relacionar con procesos celulares benignos aunque intensos, o bien a lesiones de potencial gravedad.

Se ha mostrado que la clasificación cualitativa de ASCUS puede ser aclarada mediante medidas matemáticas objetivas y reproducibles, que permitan un diagnóstico objetivo, superando la dificultad originada por la observación cualitativa, en la distinción morfológica entre alteraciones benignas y lesiones potencialmente graves, como se mostró en el desarrollo de la metodología diagnóstica, que permitió diferenciar, matemáticamente, ASCUS asociadas a una reacción normal de las que están involucradas con lesión intraepitelial, evidenciando que este estadio no presenta características matemáticas diferenciales, sino que puede mostrar características ya sea de normalidad o de LEIBG (Rodríguez, 2011). En dicho trabajo, se establecieron medidas fractales del núcleo, del citoplasma y de la totalidad celular, evaluadas mediante el concepto de variabilidad y de Armonía Matemática Intrínseca (AMI) celular de dimensiones fractales (Rodríguez et al. 2010; Rodríguez, 2011), pues se evidenció que solamente con las dimensiones fractales de las células no se lograba una caracterización aplicable a la clínica (Rodríguez et al. 2006). Este concepto permitió diferenciar, matemáticamente, normalidad de LEIBG de manera objetiva y reproducible, proporcionando un diagnóstico específico para cada caso particular, independientemente de consideraciones estadísticas, al estar basado en una forma de pensamiento universalista, que busca características matemáticas presentes en cualquier célula posible del epitelio escamoso cervical. Gracias a este concepto físico-matemático fue posible desarrollar, posteriormente, una generalización, mostrando todos los prototipos celulares posibles, desde normalidad hasta cáncer (Rodríguez et al. 2010), los cuales, fueron contrastados con células reales, evidenciando que sus medidas estaban incluidas dentro de la generalización y que habían sido correctamente diagnosticadas.

En este contexto, el objetivo de este trabajo fue desarrollar trayectorias de posible alteración celular, desde normalidad hasta ASCUS, tanto con medidas análogas a normalidad como a LEIBG, con base en el concepto de Armonía Matemática Intrínseca (AMI) celular de dimensiones fractales (Rodríguez et al. 2010; Rodríguez, 2011), de tal forma que constituyan una herramienta de ayuda en el seguimiento temporal de pacientes que presenten ASCUS.

MATERIALES Y MÉTODOS

Se tomaron imágenes de tres células escamosas de cuello uterino diagnosticadas como normales por un patólogo experto, provenientes de un archivo personal del grupo Insight. Las células, se fotografiaron con cámara digital (Nikon), a través de microscopio (Nikon Eclipse ε200), con aumento de 100X, obteniendo imágenes con dimensiones de 1200 x 1600 píxeles. Las fotografías, se importaron a un editor de imágenes, para su posterior análisis.

Se calculó la dimensión fractal del borde de la membrana celular, denominada C, de la membrana nuclear N y de la totalidad T de la célula, mediante la aplicación del método de box Counting (Rodríguez, 2011; Rodríguez et al. 2010). Para la aplicación de este método, superpusieron dos rejillas a las imágenes medidas, donde el lado de una es exactamente el doble del lado de la otra y se realizó un conteo del número de cuadros que son tocados por los bordes de cada uno de los objetos medidos. Estos valores son utilizados para el cálculo de la dimensión fractal, de acuerdo con la siguiente ecuación:

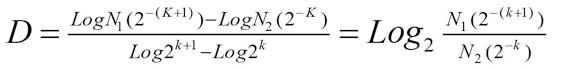
donde:

D: Dimensión fractal.

N: Número de cuadros que contiene el contorno del objeto.

K: Grado de partición de la cuadrícula.

Con base en estas medidas, se calculó la AMI celular y variabilidad, definida como la resta en la primera cifra posterior a la coma en la dimensión fractal de dos de los tres objetos evaluados; mediante esta medida es posible comparar cuantitativamente la relación entre las partes y la totalidad de la célula, diferenciando normalidad de anormalidad (Tabla 1).

Teniendo en cuenta que la metodología previamente desarrollada (Rodríguez, 2011) evidencia que las células ASCUS no presentan características matemáticas que las diferencien de normalidad o de LEIBG, sino que pueden presentar valores matemáticos de AMI celular y variabilidad de la dimensión fractal correspondientes a uno u otro de estos estados, con base en las medidas fractales obtenidas de Núcleo, de Citoplasma y de la Totalidad para las células normales, se realizaron tres simulaciones de trayectorias de la posible alteración geométrica de cada una hacia células ASCUS, las cuales, pueden presentar medidas matemáticas de AMI celular y variabilidad, correspondientes a una célula de normalidad o bien a una LEIBG.

Para ello, se observaron cada una de las células normales en el espacio de Box Counting y se realizaron variaciones geométricas del borde de cada uno de los objetos medidos, de tal modo que, simultáneamente, se producía una variación en el número de espacios ocupados en cada una de las rejillas. Estas variaciones, se realizaron de tal modo que mantuvieran dimensiones fractales, cuyas medidas de AMI celular y variabilidad correspondieran con cada una de las condiciones buscadas, es decir, que tuvieran medidas matemáticas como las que se encontraron previamente en ASCUS, que podían ser análogas a normalidad o a LEIBG. De este modo, se obtuvieron nuevas células, que mantenían las relaciones estructurales de AMI celular y variabilidad y que, al estar basadas en las células normales, medidas experimentalmente, constituyen posibles formas que puede tomar la célula en un proceso de alteración celular que desemboque en la aparición de células ASCUS, independientemente de repeticiones del experimento o de análisis estadísticos.

RESULTADOS Y DISCUSIÓN

Este es el primer trabajo, en el que se establecen simulaciones de posibles trayectorias de alteración de una célula normal hacia una célula ASCUS, con base en el concepto de AMI celular y Variabilidad, se realizaron variaciones geométricas en el espacio de Box Counting de tres objetos: el núcleo, el citoplasma sin núcleo y la totalidad de las células normales, manteniendo las relaciones matemáticas de AMI celular y Variabilidad entre los objetos medidos, simulando trayectorias hacia ASCUS con medidas matemáticas análogas, tanto a normalidad como a L-SIL. Esta metodología evidencia la posibilidad de establecer rutas geométricas de alteración celular con implicaciones clínicas, permitiendo establecer la cercanía matemática de una ASCUS con una célula normal o con una L-SIL y, de este modo, hacer seguimientos en el tiempo, que sirvan como indicadores tempranos del progreso de pacientes que presenten ASCUS.

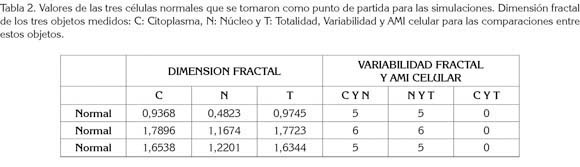
Las dimensiones fractales del contorno celular de las tres células normales medidas estuvieron entre 0,9368 y 1,7896; para el contorno nuclear, se encontró que las dimensiones fractales estuvieron entre 0,4823 y 1,2201 y para la totalidad, se obtuvieron valores entre 0,9745 y 1,7723. Los valores de variabilidad y AMI de la comparación entre Citoplasma y Núcleo, se hallaron entre 4 y 6, al igual que entre Núcleo y Totalidad, mientras que para la comparación entre Citoplasma y Totalidad, se obtuvieron valores de 0 en los tres casos (Tabla 2).

Las simulaciones presentaron valores de dimensión fractal entre 0,4123 y 1,9524, para el citoplasma; entre 0,1678 y 1,5616, para el núcleo y entre 0,4392 y 1,8234, para la totalidad. Los valores de variabilidad y AMI de la comparación entre Citoplasma y Núcleo oscilaron entre 1 y 5, mientras que presentaron valores entre 1 y 4, entre Núcleo y Totalidad y entre Citoplasma y Totalidad, se obtuvieron valores entre 0 y 2 (Tabla 3).

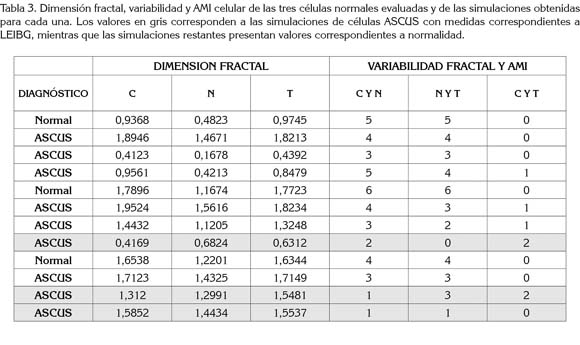
En el caso de la primera célula, las simulaciones obtenidas de ASCUS presentaron valores análogos a una célula normal en todos los casos. En la segunda, la tercera de las simulaciones obtenidas de ASCUS presentó valores análogos a una célula L-SIL, mientras que las dos primeras mostraron valores similares a normalidad. En la tercera célula, la primera simulación reveló valores similares a normalidad, mientras que las dos restantes indicaron valores relacionados con L- SIL (Tabla 3). Cabe anotar que en este trabajo no se ejecutaron simulaciones respecto a ASC-H.

Si bien los resultados obtenidos evidencian que existe una relación entre la disminución de los valores de variabilidad y AMI celular y el aumento de la gravedad de las alteraciones preneoplásicas, confirmando los hallazgos previos (Rodríguez et al. 2010; Rodríguez, 2011), no se puede establecer una única trayectoria posible de la alteración geométrica de cada una de las células medidas, pues desde la perspectiva física y matemática, en este fenómeno, no se tienen relaciones de causa consecuencia secuenciales temporalmente, sino que el fenómeno puede ser descrito desde ''ventanas temporales'' que, en este caso, son cada una de las simulaciones realizadas para cada célula normal.

La idea de ventana temporal, acuñada por Prigogine (Fernández, 1990), implica que no se puede tener medidas continuas de este fenómeno; sin embargo, su estudio desde esta perspectiva acausal permite evidenciar armonías subyacentes a las alteraciones celulares independientemente de la edad, de los factores de riesgo o de cualquier análisis poblacional, siendo aplicables a cada caso particular. En la práctica clínica diaria esto sería muy útil, pues aunque se pueden presentar diferentes posibilidades de alteración celular hacia enfermedad o normalidad de pacientes que presenten ASCUS, el establecimiento de parámetros matemáticos que den cuenta de estas alteraciones, indicando cuantitativamente su cercanía a uno u otro estado, ayudaría a tener un criterio más preciso acerca de la pertinencia y la necesidad de la realización de seguimientos en el tiempo de pacientes que presenten ASCUS, en especial, si manifiestan valores cercanos a L-SIL.

Algunas medidas, como la toma seriada de CCV, han logrado mejorar la sensibilidad y disminuir el impacto de falsos negativos (Guilbert et al. 2007), pero también se han desarrollado nuevas técnicas automatizadas, para complementar el tamizaje manual; dos de ellas son el sistema de Pap-net y la citología en medio líquido (Thin Prep Pap Test). El primero es un lector de placas sistematizado, que utiliza redes neurales para realizar un segundo tamizaje a los frotis diagnosticados como negativos (Dybowski & Gant, 1995; Prismatic Project Management Team, 1999). El segundo es una alternativa de preparación en medio líquido, donde el dispositivo de recolección se enjuaga en un tubo con una solución conservante, antes de ser enviado al laboratorio; luego, la muestra se centrifuga, se extrae la sangre y el moco, se retira el sedimento celular y se suspende en un diluyente y, finalmente, se hace un frotis en la lámina (Alameda et al. 2007); no obstante, aunque estas nuevas técnicas muestran una mejor especificidad (Dybowski & Gant 1995; Prismatic Project Management Team, 1999; Alameda et al. 2007), también aumentan el costo del cribado.

Estos problemas son especialmente significativos en el caso de las células denominadas ASCUS, definidas como alteraciones celulares potencialmente graves, pero de las cuales no se puede realizar una afirmación concluyente (Lacruz, 2003). Esta categoría es la que constituye un mayor reto a nivel diagnóstico, pues es la que presenta menor reproducibilidad inter-observador (Smith et al. 2000; Stoler & Schiffman, 2001; Lachman & Cavallo-Calvanese, 1998). En estos casos, es necesario invertir mayores recursos para la determinación de un diagnóstico, utilizando exámenes adicionales, como colposcopia y biopsia, sin que garantice un diagnóstico certero, dado que los resultados pueden no correlacionarse adecuadamente, lo que dificulta, en gran medida, la posibilidad de hacer pronósticos útiles.

En este contexto, el estudio de las trayectorias posibles de normalidad hacia ASCUS constituye un tema de gran importancia y puede tener gran utilidad a nivel clínico a futuro, especialmente, teniendo en cuenta el bajo costo y la amplia cobertura de la citología en la actualidad. Es necesario realizar estudios posteriores con base en los resultados obtenidos en el presente trabajo, con el fin de desarrollar trayectorias de aplicación clínica, mediante una metodología objetiva, reproducible y de fácil aplicación, que pueda disminuir los costos, no solamente en la detección de lesiones cervicales sino en el seguimiento de casos de potencial gravedad y en la evaluación de medicamentos o terapias instauradas.

Este trabajo está basado en una perspectiva innovadora de investigación en medicina, donde se trabaja a partir de los principios y las formas de pensamiento de las teorías físicas y matemáticas para llegar a afirmaciones de validez universal y de aplicación clínica, a cada caso particular. La forma de razonamiento inductivo utilizado en la física y la matemática permite, a partir de unos pocos casos, establecer relaciones matemáticas de universales de utilidad para casos particulares. En medicina ha sido posible establecer leyes, a partir de las cuales es posible establecer la totalidad de posibilidades que se pueden dar en la práctica de fenómenos tan complejos, como la dinámica cardiaca (Rodríguez et al. 2013), células de cuello uterino (Rodríguez et al. 2010; Rodríguez, 2011) o la totalidad de posibles arterias en el proceso de restenosis, evidenciando cómo a partir de pocos casos y con relaciones matemáticas se puede mostrar cómo cambian las relaciones estructurales fractales finitas, acotadas en el intervalo numérico entre 0-2 en el espacio finito Box Counting, determinando objetiva y cuantitativamente cualquier estado posible (Rodríguez et al. 2010). Este tipo de investigaciones en las que se hace uso de teorías físicas y matemáticas para la dilucidación y solución de problemas en medicina ha proporcionado soluciones a diferentes problemas de la práctica médica actual, en áreas tan diversas, como la cardiología (Rodríguez et al. 2007; Rodríguez, 2010a; Rodríguez, 2012), la biología molecular (Rodríguez et al. 2010), la inmunología (Rodríguez, 2008), la predicción de epidemias (Rodríguez, 2010b) y la infectología (Rodríguez et al. 2012), evidenciando la importancia de esta perspectiva, tanto a nivel experimental o predictivo como a nivel clínico, como es el caso del presente trabajo, donde se abre una nueva perspectiva para el seguimiento clínico de alteraciones preneoplásicas de potencial gravedad.

Agradecimientos: Al Doctor Héctor Posso, docente de la Universidad Militar Nueva Granada y a la Liga Contra el Cáncer, por su apoyo a nuestras investigaciones. A la Vicerrectoría de Investigaciones y al Fondo de Investigaciones, por el apoyo y financiación de este trabajo, especialmente, a las Doctoras Jacqueline Blanco, Vicerrectora de Investigaciones, Martha Bahamón, Vicerrectora Académica, Esperanza Fajardo, Directora del Centro de Investigaciones de la Facultad de Medicina y a los Doctores Juan Miguel Estrada, Decano de la Facultad de Medicina, Mario Alejandro Castro, Jefe de la División de Investigación Científica y a Henry Acuña, por su apoyo a nuestras investigaciones. Al Centro de investigaciones de la Clínica del Country, especialmente, al Doctor Tito Tulio Roa, Director de Educación Médica; al Doctor Alfonso Correa, Director del Centro de Investigaciones, al Doctor Jorge Ospina, Director Médico; a la Doctora Adriana Lizbeth Ortiz, Epidemióloga y a Silvia Ortiz, por su apoyo constante. Conflicto de Intereses: El manuscrito fue preparado y revisado con la participación de todos los autores, quienes declaramos que no existe ningún conflicto de intereses que ponga en riesgo la validez de los resultados presentados. Financiación: Este trabajo hace parte de los resultados del proyecto ING - 1070 financiado por el Fondo de Investigaciones de la Universidad Militar Nueva Granada.

BIBLIOGRAFÍA

1. ALAMEDA, F.; FUSTÉ, P.; ALBERT, S.; ROMERO, E.; GIMFERER, E.; SOLER, I.; CONANGLA, M.; CARRERAS, R.; SERRANO, S. 2007. Citología en medio líquido (Thin Prep Pap Test). Un año de experiencia. Prog. Obstet. Ginecol. (España). 50:197-202.

2. BAISH, J.; JAIN, R. 2000. Fractals and Cancer. Cancer Res. (EstadosUnidos). 60:3683- 3688.

3. BASSINGTHWAIGHTE, J.; LIEBOVITCH, L.; WEST, B. 1994. Fractal Physiology . Ed. American Physiological Society by Oxford University Press. (New York). p.210-228.

4. CHENG, S.C.; HUANG, Y.M. 2003. A novel approach to diagnose diabetes based on the fractal characteristics of retinal images. IEEE Trans Inf. Technol. Biomed. (EstadosUnidos). 7(3):163-70.

5. CORREA, C.; RODRÍGUEZ, J.; PRIETO, S.; BERNAL, P.; OSPINO, B.; MUNÉVAR, A.; ÁLVAREZ, L.; MORA, J.; VITERY, S. 2012. Geometric diagnosis of erythrocyte morphophysiology. JMMS. (Nigeria). 3(11):715-720.

6. DIM, C.C. 2012. Towards improving cervical cancer screening in Nigeria: A review of the basics of cervical neoplasm and cytology. Niger J. Clin. Pract. (India). 15:247-252.

7. DYBOWSKI, R.; GANT, V. 1995. Artificial neural networks in pathology and medical laboratories. Lancet. (Estados Unidos). 346:1203-1207.

8. EDITORIAL COMMITE OF ACTA CYTOL. 1993. The Bethesda System for Reporting Cervical/Vaginal Cytologyc Diagnoses. Acta Cytol. 37: 115.

9. FERNÁNDEZ, A. 1990. Introducción. En: FERNÁNDEZ, A. Orden y Caos. Ed. Prensa Científica S.A. (España). p.4-8.

10. GARTE, S. 2004. Fractal properties of the human genome. J. Theor. Biol. (Inglaterra). 230(2):251-60.

11. GOLDBERGER, A.L.; RIGNEY, D.R.; WEST, B.J. 1990. Chaos and fractals in human physiology. Sci. Am. 262:42-49.

12. GOLDBERGER, A.; AMARAL, L.; HAUSDORFF, J.; IVANOV, P.; PENG, CH.; STANLEY, H.E. 2002. Fractal dynamics in physiology: alterations with disease and aging. PNAS. (Estados Unidos). 99:2466-2472.

13. GUILBERT, E.; BORODITSKY, R.; BLACK, A.; KIVES, S.; LEBOEUF, M.; MIROSH, M.; SENIKAS, V.; WAGNER, M.S.; WEIR, E.; YORK-LOWRY, J.; REID, R.; TRUSSELL, J.; SOCIETY OF OBSTETRICIANS AND GYNAECOLOGISTS OF CANADA. 2007. Canadian Consensus Guideline on Continuous and Extended Hormonal Contraception, 2007. J. Obstet. Gynaecol. Can. (Canada). 29:S1-32.

14. KISELEV, V.G.; HAHN, K.R. 2003. Is the brain cortex a fractal? Neuroimage. (United States). 20(3):1765-1774.

15. LACHMAN, M.F.; CAVALLO-CALVANESE, C. 1998. Qualification of atypical squamous cells of undetermined significance in an independent laboratory: is it useful or significant? Am. J. Obstet. Gynecol. 179:421-429.

16. LACRUZ, C. 2003. Nomenclatura de las lesiones cervicales (de Papanicolau a Bethesda 2001). Rev. Esp. Patol: 36(1):5-10.

17. LUZI, P.; BIANCIARDI, G.; MIRACCO, C.; DESANTI, M.M.; DEL VECCHIO, M.T.; ALIA, L.; TOSI, P. 1999. Fractal analysis in human pathology. Ann. NY Acad. Sci. (Estados Unidos). 879:255-257.

18. MANDELBROT, B. 1967. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science, New Series. (Estados Unidos).156 (3775):636-638.

19. MAUROY, B.; FILOCHE, M.; WEIBEL, E.R.; SAPOVAL, B. 2004. An optimal bronchial tree may be dangerous. Nature. 427:633-636.

20. NANDA, K.; MCCRORY, D.C.; MYERS, E.R.; BASTIAN, L.A.; HASSELBLAD, V.; HICKCY, J.D.; MALCHAR, D.B. 2000. Accuracy of the Papanicolaou test in screening for and follow-up of cervical cytologic abnormalities: a systematic review. Ann. Intern. Med. (Estados Unidos). 132:810-819.

21. PRISMATIC PROJECT MANAGEMENT TEAM. 1999. Assessment of automated primary screening on PAPNET of cervical smears in the PRISMATIC trial. Lancet. 353(9162):1381-1385.

22. RODRÍGUEZ, J.; MARIÑO, M.; AVILÁN, N.; ECHEVERRI, D. 2002. Medidas fractales de arterias coronarias en un modelo experimental de reestenosis: Armonía matemática intrínseca de la estructura arterial. Rev. Col. Cardiol. 10 (2):65-72.

23. RODRÍGUEZ, J.; PRIETO, S.; ORTIZ, L.; WIESNER, C.; DÍAZ, M.; CORREA, C. 2006. Descripción matemática con dimensiones fractales de células normales y con anormalidades citológicas de cuello uterino. Rev. Cienc. Salud. (Colombia). 4 (2):58-63.

24. RODRÍGUEZ, J.; PRIETO, S.; ORTIZ, L.; CORREA, C.; ÁLVAREZ, L.; BERNAL, P.; CASADIEGO, E. 2007. Variabilidad de la dimensión fractal de la ramificación coronaria izquierda en ausencia y presencia de enfermedad arterial oclusiva moderada y severa. Rev. Col. Cardiol. 14(3):173-179.

25. RODRÍGUEZ, J. 2008. Teoría de unión al HLA clase II: teoría de probabilidad, combinatoria y entropía aplicadas a secuencias peptídicas. Inmunología. (España). 27(4):151-166.

26. RODRÍGUEZ, J. 2010a. Entropía Proporcional de los Sistemas Dinámicos Cardiacos: Predicciones físicas y matemáticas de la dinámica cardiaca de aplicación clínica. Rev Col. Cardiol. 17:115-129.

27. RODRÍGUEZ, J. 2010b. Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev. Panam Salud Pública. (Colombia). 27(3):211-218.

28. RODRÍGUEZ, J.; BERNAL, P.; PRIETO, S.; CORREA, C. 2010. Teoría de péptidos de alta unión de malaria al glóbulo rojo. Predicciones teóricas de nuevos péptidos de unión y mutaciones teóricas predictivas de aminoácidos críticos. Inmunología (España). 29(1):7-19.

29. RODRIGUEZ, J.; PRIETO, S.; CORREA, C.; BERNAL, P.; PUERTA, G.; VITERY, S.; SORACIPA, Y.; MUÑOZ, D. 2010. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Med. Phys. (Inglaterra).10:1-6.

30. RODRÍGUEZ, J.; PRIETO, S.; CORREA, C.; POSSO, H.; BERNAL, P.; PUERTA, G.; VITERY, S.; ROJAS, I. 2010. Generalización fractal de células preneoplásicas y cancerígenas del epitelio escamoso cervical. Una nueva metodología de aplicación clínica. Rev. Fac. Med. (Colombia). 18 (2):173-181.

31. RODRÍGUEZ, J. 2011. Nuevo método fractal de ayuda diagnóstica para células preneoplásicas del epitelio escamoso cervical. Rev. U.D.C.A Act. & Div. Cient. (Colombia). 14(1):15-22.

32. RODRÍGUEZ, J.; PRIETO, S.; BERNAL, P.; PÉREZ, C.; CORREA, C.; ÁLVAREZ, L.; BRAVO, J.; PERDOMO, N.; FACCINI, A. 2012. Predicción de Linfocitos T CD4 con base en la teoría de probabilidad. Aplicación clínica a poblaciones de leucocitos, linfocitos y CD4 de pacientes con VIH. Infectio. (Colombia). 16(1):15-22.

33. RODRÍGUEZ, J.; PRIETO, S.; CORREA, C.; BERNAL, P.; ÁLVAREZ, L.; FORERO, G.; VITERY, S.; PUERTA, G.; ROJAS, I. 2012. Diagnóstico fractal del ventriculograma cardiaco izquierdo. Geometría fractal del ventriculograma durante la dinámica cardiaca. Rev. Col. Cardiol. 19(1):18-24.

34. RODRÍGUEZ, J.; CORREA, C.; MELO, M.; DOMÍNGUEZ, D.; PRIETO, S.; CARDONA, D.M.; SORACIPA, Y.; MORA, J. 2013. Chaotic cardiac law: Developing predictions of clinical application. J. Med. Sci. 4(2):79-84.

35. SANKAR, D.; THOMAS, T. 2010. A New Fast Fractal Modeling Approach for the Detection of Microcalcifications in Mammograms. J. Digit. Imaging. (United States). 23(5):538-546.

36. SMITH, A.E.; SHERMAN, M.E.; SCOTT, D.R.; TABBARA, S.O.; DWORKIN, L.; OLSON, J.; THOMPSON, J.; FASER, C.; SNELL, J.; SCHIFFMAN, M. 2000. Review of the Bethesda System atlas does not improve reproducibility or accuracy in the classification of atypical squamous cells of undetermined significance smears. Cancer. (Estados Unidos). 90:201-206.

37. SPENCE, A.R.; GOGGIN, P.; FRANCO, E.L. 2007. Process of care failures in invasive cervical cancer: systematic review and metaanalysis. Prev. Med. 45:93- 106.

38. STEHLÍK, M.; MRKVIČKA, T.; FILUS, J.; FILUS, L. 2012. Recent developments on testing in cancer risk: a fractal and stochastic geometry. J. Reliab. Statist. Stud. (India). 5(Issue Special):83-95.

39. STEPIEN, R.; STEPIEN, P. 2010. Analysis of Contours of Tumor Masses in Mammograms by Higuchi's Fractal Dimension. Biocybern. Biomed. Eng. (Polonia). 30(4):49-56.

40. STOLER, M.H.; SCHIFFMAN, M. 2001. Atypical Squamous Cells of Undetermined Significance-Low- grade Squamous Intraepithelial Lesion Triage Study (ALTS) Group. Interobserver reproducibility of cervical cytologic and histologic interpretations: realistic estimates for the ASCUS-LSIL Triage Study. JAMA. 285:1500-1505.

41. VASILJEVIC, J.; RELJIN, B.; SOPTA, J.; MIJUCIC, V.; TULIC, G.; RELJIN, I. 2012. Application of multifractal analysis on microscopic images in the classification of metastatic bone disease. Biomed Microdevices. (EstadosUnidos). 14:541-548.

42. WELTER, M.; RIEGER, H. 2010. Physical determinants of vascular network remodeling during tumor growth. Eur. Phys. J. E. (Francia). 33:149-163.

43. WORLD HEALTH ORGANIZATION. International Agency for Research Center. Globocan. 2008a. Fact Sheets: Cervix uteri, Worldwide. Disponible desde internet http://globocan.iarc.fr/factsheet.asp (con acceso 14/01/2013).

44. WORLD HEALTH ORGANIZATION. International Agency for Research Center. Globocan. 2008b. Online Analysis, Incidence/Mortality, Chart by populations, Cervix uteri, all ages, 20 highest in Americas. Disponible desde internet http://globocan.iarc.fr/ (con acceso 10/01/2013).

45. WEIDERPASS, E.; LABRÈCHE, F. 2012. Malignant Tumors of the Female Reproductive System. Saf. Health Work. (Corea del Sur). 3:166-180.

46. WHO/ICO. Information Centre on HPV and Cervical Cancer (HPV Information Centre). 2010. Human Papilloma virus and Related Cancers in Americas. Summary Report 2010. Disponible desde internet http://www.who.int/hpvcentre (con acceso el 01/11/2012).

Recibido: Diciembre 13 de 2012 Aceptado: Julio 9 de 2013