CIENCIAS EXACTAS Y NATURALES-Artículo Científico

RESTAURACIÓN DIGITAL DE IMÁGENES MEDIANTE ECUACIONES DIFERENCIALES PARCIALES

DIGITAL IMAGE RESTORATION BY PARTIAL DIFFERENTIAL EQUATIONS

Juan Gabriel Triana¹, Liliana Constanza Romero², Diego Gerardo Roldán³

¹ Matemático, Magister en Ciencias - Matemática Aplicada. Docente Universidad Manuela Beltrán. Departamento de Ciencias Básicas. Coordinador de Matemáticas. Av. Circunvalar No 60-00, Bogotá, D.C., Colombia, jtrianal@unal.edu.co

² Matemática, Magister en Ciencias - Matemática Aplicada (C). Universidad Nacional de Colombia, sede Bogotá, lcromerom@unal.edu.co

³ Matemático, Magister en Ciencias - Matemática Aplicada. Docente Universidad de Ciencias Aplicadas y Ambientales U.D.C.A. Facultad de Ciencias y Tecnología, Campus Universitario Calle 222 No 55-37, Bogotá, D.C., Colombia, dgroldanj@unal.edu.co

Rev. U.D.C.A Act. & Div. Cient. 16(2): 511-518, Julio-Diciembre, 2013

RESUMEN

La restauración digital de imágenes, definida como el arte de mejorar la calidad de las imágenes, ha logrado un amplio desarrollo en los últimos años, alcanzando un alto nivel de popularidad, desde que se utilizaron métodos matemáticos y computacionales para restaurar las imágenes distorsionadas, enviadas por el telescopio Hubble; sin embargo, las imágenes no siempre son afectadas de manera total, algunas sufren pérdida de información en algunas regiones, otras simplemente son afectadas por el paso del tiempo, por tanto, es necesario establecer técnicas que permitan restaurar imágenes, en las cuales, el daño no es reversible, mediante un filtro aplicado sobre toda la imagen. En este trabajo, se establece un método que permite detectar las regiones dañadas en la imagen, realizar un proceso de restauración, basado en ecuaciones diferenciales parciales, sobre las regiones dañadas, logrando, de este modo, construir la imagen recuperada. El método propuesto en este escrito podrá ser aplicado para la restauración de imágenes en blanco y negro, a color e, incluso, imágenes de obras de arte.

Palabras clave: Análisis numérico, procesamiento de imágenes, ecuación del calor.

SUMMARY

Inpainting, art of improving the image quality, has achieved great development in recent years, reaching a high level of popularity after the restoration of images sent by the Hubble telescope, through mathematical methods and computational tools. However, the images are not always totally affected, suffering some loss of information in some areas, others simply are affected by the passage of time, so it is necessary to establish techniques to restore images in which the damage is not reversible using a filter applied to the entire image. This study established a method which allows to detect the damaged regions of the image and to perform a restoration process on the damaged regions, based on partial differential equations, thus achieving the construction of a recovered image. The method proposed in this paper could be applied to the restoration of grayscale and color images and even of artwork.

Key words: Numerical analysis, image processing, heat equation.

INTRODUCCIÓN

La restauración de imágenes, conocida como ''inpainting'', es el arte de mejorar la calidad de una imagen, compensando o eliminando las distorsiones y el deterioro de la imagen. Una restauración ideal solamente puede ser llevada a cabo si el proceso de deterioro se puede describir matemáticamente (Klette & Zamperoni, 1996).

Durante el proceso de captura de una imagen suele haber efectos indeseados, conocidos como ruido; en dichos casos, se suele modelar el tipo de daño ocasionado, como una transformación que afecta la imagen, que se denomina filtro y de este modo, se puede construir una transformación inversa, para corregir el daño generado (Klette & Zamperoni, 1996); no obstante, cuando el daño no afecta a toda la imagen, sino parte de ella, como es el caso de imágenes en las que algunas partes han sido recortadas, imágenes sobre las cuales el paso del tiempo ha hecho estragos, imágenes con la fecha de registro, en casos como estos, aplicar un filtro sobre la imagen completa no es conveniente, ya que las regiones donde no se presenta daño también serían modificadas (Bertozzi & Schönlieb, 2011), por esta razón, es necesario diseñar una estrategia que permita detectar las regiones dañadas en la imagen y llevar a cabo el proceso de restauración, solamente sobre dichas regiones.

Una imagen, matemáticamente, puede ser descrita mediante una función que toma un punto de la imagen, , y le asigna un valor numérico ; de este modo, la terna se denominará pixel (Klette & Zamperoni, 1996). El pixel se define, usualmente, como la menor unidad homogénea de color; sin embargo, si una imagen se amplía lo suficiente se podrán visualizar los pixeles y, cuando esto ocurre, se dice que la imagen presenta pixelamiento.

Considerando una imagen, es posible tomar una cuadrícula uniforme, de tal manera que cada cuadro representa un pixel y al unir todos los pixeles, se obtendrá la imagen completa, de este modo, una imagen podrá ser descrita mediante una matriz de pixeles (Esakkirajan et al. 2011); normalmente, un pixel es de tamaño pequeño, en comparación con toda la imagen, por esta razón, es de esperarse que la representación matricial de una imagen sea de un tamaño considerablemente grande.

En el caso en que la imagen es representada en blanco y negro o en escala de grises, cada pixel guarda la información de la intensidad de brillo que corresponde a la ubicación en la matriz que este ocupa (Jähne, 2005) (Imagen 1).

En la imagen anterior, el valor es la intensidad almacenada en el pixel que se encuentra en la posición . El tamaño de la imagen es dado por , que corresponden al número de pixeles de alto y de ancho de la imagen.

Cuando la imagen se encuentra a color, la representación descrita no es suficiente, ya que una matriz no basta para mostrar todos los colores, por lo tanto, es necesario interpretar la imagen mediante tres matrices (conocidas como máscaras), las cuales, representan la intensidad de tres colores específicos. Esta representación, a través de las máscaras mencionadas, puede ser realizada mediante diversos formatos; en particular, para imágenes digitales, se suele utilizar RGB, constituida por los colores rojo(R), verde(G) y azul(B) (Pratt, 2001) (Imagen 2).

Cabe destacar que las matrices R,G,B, correspondientes a cada una de las máscaras, son de filas y columnas, pues la imagen asociada a ellas contiene pixeles.

El manejo, a través de las tres máscaras, es coherente, ya que a partir de estas es posible generar los colores primarios (amarillo, azul, rojo); el blanco, al tomar la máxima intensidad de los tonos y, el negro, al considerar la ausencia en la intensidad de cada tono. La información de cada pixel, se encuentra restringida al formato en que se halle la imagen; por ejemplo, en el caso de una imagen en formato JPG, cada pixel puede almacenar 8 bits de información numérica, por lo tanto, está en capacidad de tomar 2⁸ posibles valores, de donde se obtiene que la información de los pixeles varía entre 0, para la mínima intensidad y 255, para la máxima intensidad (Petrou & Petrou, 2010).

En este escrito, se muestra cómo se realiza la construcción de la estrategia de restauración, además, se observa el funcionamiento del método al aplicarse sobre imágenes en escala de grises (blanco y negro) y a color, las cuales, presentan pérdida de información en algunas regiones, que no siempre son definidas mediante formas regulares; también se muestra cómo el método logra determinar y clasificar las regiones deterioradas de la imagen.

MATERIALES Y MÉTODOS

La descripción matemática de una imagen, se lleva a cabo mediante el uso de matrices; la detección de las regiones dañadas de la imagen, se realiza por la aplicación de un filtro de detección de bordes, que permite diferenciar regiones dañadas de regiones en buen estado.

Los bordes en una imagen son percibidos por el ojo humano, como un cambio en la intensidad o el color, en ciertas regiones de la imagen. El conocimiento de los bordes de la imagen es necesario, para poder aplicar la técnica de restauración, por esta razón, se requiere diferenciarlos del resto de la imagen; para ello, se representan los bordes, mediante el color blanco, mientras el resto de la imagen, con color negro; esta técnica es conocida como binarización (Burger & Burge, 2009), que permite localizar fácilmente los bordes. En particular, si el borde representa una región cerrada, se podrá concluir si corresponde a una región, en la cual, existe un daño de algún tipo o se presenta una pérdida total de información.

El rastreo de los bordes de una imagen no es una técnica simple, existen diversos algoritmos y técnicas de filtros de detección de bordes, entre ellos, están los siguientes: Prewitt, Roberts, Laplaciano, Sobel, Canny (Pratt, 2001). En este documento, se aplicará el filtro Canny, ya que permite detectar bordes fuertes y bordes débiles, además, de minimizar la probabilidad de detección de bordes falsos, ocasionados por ruido en la imagen (Canny, 1986).

El método de restauración que se aplica está basado en la ecuación del calor, descrita en 1822, por Joseph Fourier, quién concluyó que, dada la información de la tasa de cambio de la temperatura en el tiempo y ciertas condiciones iniciales, es posible obtener una ecuación que describa el comportamiento de la temperatura en un cuerpo (Weinberger, 2005), que es dada por:

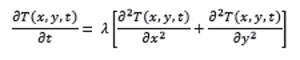
Donde λ, se denomina constante de conductividad térmica del material, x, y son las variables espaciales, t es la variable temporal, T representa la temperatura que se obtiene en el punto x, y en el instante.

La ecuación del calor, se aplica para realizar procesos de difusión en la imagen (Sangeetha et al. 2011), por ello, permite transmitir información de pixeles de regiones, en buen estado, hacia las regiones de daño.

La ecuación del calor considera el tiempo como parámetro, en este caso particular, el tiempo será utilizado, de manera discreta, como el número de iteraciones que se aplica del método propuesto. El proceso de aplicación de la ecuación del calor sobre la imagen, se lleva a cabo mediante la implementación de métodos numéricos (Burden & Faires, 2002); para tal fin, se podrían escoger diferentes métodos: los implícitos, como el método de Crank-Nicolson (Crank & Nicolson, 1947), que es un método implícito de orden 2, incondicionalmente estable para la ecuación de calor (Thomas, 1995); sin embargo, considerar métodos implícitos implicaría aumentar el costo computacional, además de requerir un planteamiento más complejo de la implementación del algoritmo, en este caso, mediante el software Matlab, en comparación con el método explícito, que es obtenido al aplicar esquemas de diferencias finitas (Canale & Chapra, 2007).

El método explícito, se obtiene al considerar la siguiente discretización en diferencias finitas de la ecuación del calor:

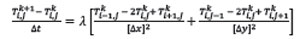
Donde T es la matriz asociada a la imagen a restaurar. Cabe destacar=que este método se considera estable si 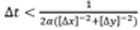(Sewell, 2005).

Debido a que el tiempo es dado por el número de iteraciones a aplicar y que cada componente de la matriz representa un pixel, se puede considerar los valores Δt=Δx=Δy=1 obteniendo así la fórmula explícita:

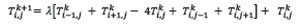
Este esquema de diferencias es estable si α<¼, por tal razón, basta considerar 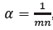, donde m y n corresponde al número de filas y columnas de la matriz T, respectivamente.

RESULTADOS Y DISCUSIÓN

El criterio de restauración, se basa en la idea de que los pixeles deteriorados o partes de la imagen donde se presentó pérdida de información, pueden estar rodeados de pixeles en perfecto estado, de los cuales, se podrá tomar información para predecir la intensidad que tenía cada pixel deteriorado (Klette & Zamperoni, 1996), de este modo, se conseguirá describir el proceso de restauración de imágenes, mediante el siguiente algoritmo: representar la imagen matemáticamente, procesar la imagen para detectar los bordes que la componen, binarizar la imagen, con el fin de identificar los bordes, identificar los bordes que corresponden a regiones en las que se presenta pérdida de información, rellenar las regiones de daño y aplicar la ecuación del calor, para realizar el proceso de difusión de información de los pixeles que rodean las regiones de daño.

La restauración de la imagen, se realiza mediante la ecuación del calor, los demás pasos, se llevan a cabo para detectar las regiones de la imagen que deben ser restauradas. El proceso de restauración, se efectúa únicamente sobre las regiones de daño, en dos etapas: en la primera, cada pixel de la región de daño se restaura con la información de los pixeles contiguos que no se encuentran en dicha región; en la segunda etapa, los pixeles toman información de los pixeles vecinos, incluso,aquellos dentro de la región de daño, esto con el fin de dar mayor solidez y uniformidad al color que toman las regiones de daño.

Se debe mencionar que la ecuación del calor es una ecuación diferencial parabólica (Fritz, 1981) y, por tal motivo, presenta estado estacionario (Gockenbach, 2002); esto se traduce, en que después de cierto número de iteraciones, el nuevo resultado no va a diferir considerablemente del resultado anterior.

El estado estacionario también advierte que no es buena idea aplicar la ecuación del calor sobre toda la imagen, ya que la imagen se ira degradando, hasta que al final, todos los pixeles, alcanzan el color promedio de la imagen (Kimia & Siddqi, 1996).

Para llevar a cabo el proceso de validación del método de restauración, se considera una imagen en blanco y negro, en perfecto estado, sobre la que se realizan algunos cortes, generando, de este modo, algunas regiones de daño con pérdida total de información. La imagen con las regiones recortadas será restaurada, de tal manera que, al final, se de generar las regiones de daño (Imagen 3).

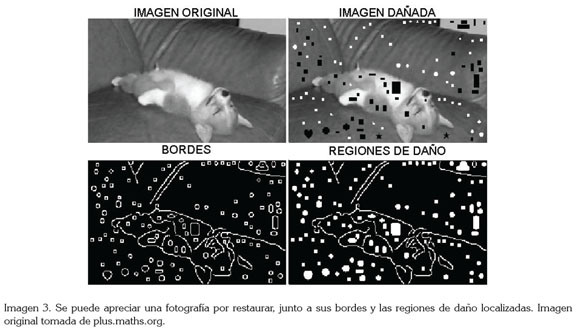
De la imagen 3, se observa el original junto con la imagen después de aplicar daños sobre algunas regiones; en la parte inferior, se observan los resultados al aplicar el filtro de detección de bordes Canny (1986). En la parte inferior derecha, se percibe cómo los bordes permiten rastrear las regiones de daño, las cuales, una vez ubicadas, se rellenan para distinguirlas del resto de la imagen, permitiendo identificar sobre qué lugares se va a aplicar la restauración.

Al aplicar la ecuación del calor, se está migrando la información de los pixeles; durante la primera iteración, los puntos del interior de la región de daño tomarán la información de los pixeles más cercanos, que no presentan daño; sin embargo, en las demás iteraciones, tomarán la información de los pixeles contiguos (Imagen 4).

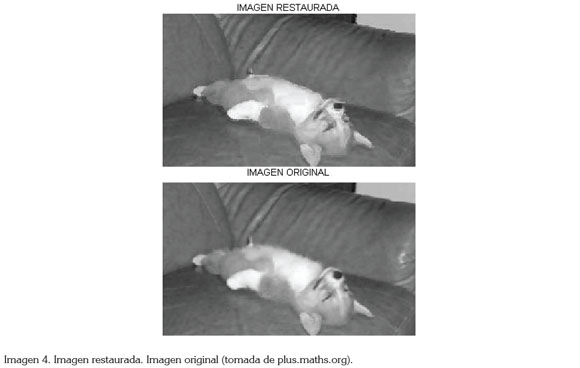
En la imagen 4, se puede comparar la imagen original con la imagen obtenida mediante la técnica de restauración; cabe destacar la leve difusión de los bordes de la imagen restaurada, lo cual, es consecuencia de la aplicación de la ecuación del calor (Weickert, 2001).

Para cuantificar el daño ocasionado, se calcula el error relativo, como la distancia Frobenius (Gerald & Wheatley, 2004), de la matriz asociada a la imagen original con la matriz asociada a la imagen dañada, sobre la norma Frobenius de la matriz original, obteniendo, de este modo, los resultados indicados en la tabla 1.

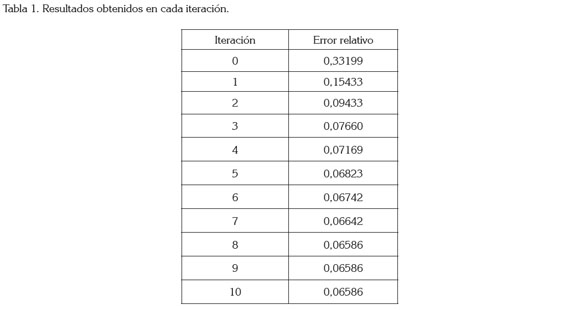
En la tabla anterior, se observa el error relativo en la restauración de la imagen en cada iteración; se puede apreciar que, a medida que aumenta el número de iteraciones, el error relativo disminuye; no obstante, a partir de la iteración 8, el error relativo no cambia, debido a que la ecuación del calor presenta estado estacionario y a la estabilidad del método aplicado, por tal razón, se puede concluir que la imagen ha quedado restaurada; el hecho de que el error relativo sea diferente de 0 es debido a que la ecuación del calor ha ocasionado un efecto leve de difusión en los bordes de la imagen; sin embargo, la validación del método de restauración se ha llevado a cabo con un problema bastante simplificado, una imagen en blanco y negro con regiones de daño generadas por formas geométricas; inmediatamente, surgen interrogantes acerca de la validez del método y si se obtendrán resultados satisfactorios, al considerar una imagen a color, cuyas regiones de daño sean generadas a partir de figuras irregulares.

Es necesario aplicar el método sobre una imagen que no haya sido deteriorada intencionalmente, por ejemplo, una imagen tomada de una obra que debe ser restaurada.

Se considera uno de los murales correspondiente a los frescos de Neidhart, que fueron pintados a finales del siglo XIV, en el salón de banquetes del comerciante Michel Menschein; sin embargo, dueños posteriores decidieron cubrir las obras con capas de yeso y pintura, dejándolas totalmente cubiertas. En 1979, durante una remodelación fueron descubiertas las obras, lastimosamente, no se encontraban en muy buen estado, debido a que pasaron alrededor de tres siglos ocultas, siendo necesaria la intervención de restauradores de arte.

La restauración de los frescos de Neidhart fue de gran importancia cultural, ya que representan el ejemplo más antiguo de pintura mural, no religiosa, en Viena (Höhle & Ottersböck, 1996); además de ser una ventana al pasado, que permite conocer parte de la sociedad medieval del siglo XIV; estas obras forman parte de la colección del Wien Museum.

A continuación, se realiza el proceso de restauración sobre un fragmento de uno de los frescos, del mismo modo en que se procedió con la imagen en blanco y negro. El procesamiento de la imagen, se efectúa mediante la construcción de las matrices RGB y para la detección de los bordes de la imagen, se aplicará nuevamente el filtro Canny, puesto que se ha comprobado que funciona de manera eficiente sobre imágenes a color (Canny, 1986). El proceso de restauración de la imagen en blanco y negro será también utilizado para la restauración de la imagen a color, de este modo, se llevará a cabo el procesamiento, máscara por máscara, de manera automática (Imagen 5).

Los resultados obtenidos sobre la imagen 5 muestran que, incluso con las geometrías intrincadas que presentan las regiones de daño en esta imagen, se lleva a cabo la restauración; sin embargo, algunas zonas no lograron ser identificadas como regiones de daño; en esos casos, en los que la restauración no es automática, se puede considerar la región afectada y realizar el proceso de difusión directamente, lo cual, queda descrito como un problema de Dirichlet (Larsson & Thomée, 2009).

Se debe mencionar que la calidad de la imagen es baja, además, que los colores no son muy intensos, debido al tiempo en que los frescos estuvieron bajo yeso, por tal razón, es de esperar un poco de sensibilidad en el rastreo de las regiones de daño ocasionada, principalmente, por el filtro de detección de bordes (Canny, 1986).

La técnica descrita no es la única manera de llevar a cabo una restauración, como también es preciso aclarar que el método numérico, utilizado para resolver la ecuación diferencial parcial propuesta, no es el único que permite llevar a cabo este trabajo (Burger et al. 2009).

En trabajos futuros, es necesario contar con un filtro de detección de bordes más poderoso, como también se puede considerar la aplicación de una técnica que permita realizar la restauración, sin generar efectos de pérdida de calidad en los bordes (Weickert, 2001).

Conflicto de intereses: El manuscrito fue preparado y revisado con la participación de todos los autores, quienes declaramos que no existe ningún conflicto de intereses, que ponga en riesgo la validez de los resultados presentados.

BIBLIOGRAFÍA

1. BERTOZZI, A.; SCHÖNLIEB, C. 2011. Unconditionally stable schemes for higher order inpainting. Comm. Math. Sci. (Estados Unidos). 9(2):413-457.

2. BURDEN, R.; FAIRES, J. 2002. Análisis Numérico 7ª ed. Ed. International Thompson Editores S.A. Méjico. 838p.

3. BURGER, M.; HE, L.; SCHÖNLIEB, C. 2009. Inpainting and a generalization for grayvalue images. SIAM J. Im. Sci. (Estados Unidos). 2(4):1129-1167.

4. BURGER, W.; BURGE, N. 2009. Principles of digital image processing. Ed. Springer-Verlag. Inglaterra. 260p.

5. CANALE, R.; CHAPRA, S. 2007. Métodos Numéricos para ingenieros. Ed. Mc Graw Hill. Méjico. 977p.

6. CANNY, J. 1986. A Computational Approach to Edge Detection. P A Mach. Int. Estados Unidos. 8(6):679- 698.

7. CRANK, J.; NICOLSON, P. 1947. A practical method for numerical evaluation of partial differential equations of the heat-conduction type. Math. Proc. Camb. Phil. Soc. (Inglaterra). 43(1):50-67.

8. ESAKKIRAJAN, T.; JAYARAMAN, S.; VEERAKUMAR, T. 2011. Digital image processing. Tata Mc Graw Hill. India. 723p.

9. FOURIER, J.B.J. 1822. Théorie analytique de la chaleur. Firmin Didot, Paris. 639p.

10. FRITZ, J. 1981. Partial differential equations. Ed. Springer. Estados Unidos. 249p.

11. GERALD, C.; WHEATLEY, P. 2004. Applied numerical analysis. Addison-Wesley. Estados Unidos. 609p

12. GOCKENBACH, M. 2002. Partial differential equations analytical and numerical methods. SIAM. Estados Unidos. 674p.

13. HÖHLE, E.; OTTERSBÖCK, B. 1996. The Neidhart Frescoes, Ca. 1400: The oldest secular mural painting in Vienna. Museums of the City of Vienna. Austria. 36p.

14. JÄHNE, B. 2005. Digital image processing. Springer. Alemania. 607p.

15. KIMIA, B.; SIDDQI, K. 1996. Geometric heat equation and nonlinear diffusion of shapes and images. Comp. vision and image understanding. (Canada). 43(1):50-67.

16. KLETTE, R.; ZAMPERONI, P. 1996. Handbook of image processing operator. Ed. John Wiley & Sons. Inglaterra. 397p.

17. LARSSON, S.; THOMÉE, V. 2009. Partial differential equations with numerical methods. Springer Verlag (Alemania). 87p.

18. PETROU, M.; PETROU, C. 2010. Image processing: The fundamental. John Wiley & Sons. Estados Unidos. 818p.

19. PRATT, W. 2001. Digital image processing. John Wiley & Sons. Estados Unidos. 738p.

20. SANGEETHA, K.; SENGOTTUVELAN, P.; BALAMURUGAN, E. 2011. Comparative analysis and evaluation of image imprinting algorithms. J. Inf. Eng. Appl. (Estados Unidos). 1(5):13-23.

21. SEWELL, G. 2005. The numerical solution of ordinary and partial differential equations. John Wiley & Sons. Estados Unidos. 352p.

22. THOMAS, J. 1995. Numerical partial differential equations, finite difference methods. Springer-Verlag. Alemania. 460p.

23. WEICKERT, J. 2001. Anisotropic diffusion in image processing. European consortium for mathematics in industry. Alemania. 170p.

24. WEINBERGER, H. 2005. Ecuaciones diferenciales en derivadas parciales. Editorial Reverté (España). 481p.

Recibido: Noviembre 6 de 2012 Aceptado: Octubre 3 de 2013