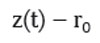
CIENCIAS EXACTAS Y NATURALES-Artículo Científico

UNA TÉCNICA DE PERSECUCIÓN UTILIZANDO MIMETISMO NO CONVENCIONAL

A PERSECUTION TECHNIQUE USING UNCONVENTIONAL MIMICRY

Juan Gabriel Triana¹, Diego Gerardo Roldán²

¹Matemático, Magister en Ciencias Matemática Aplicada. Profesor Universidad Manuela Beltrán. Departamento de Ciencias Básicas. Coordinador de Matemáticas. Av. Circunvalar No 60-00 Bogotá D.C. Colombia, e-mail: jtrianal@unal.edu.co

Rev. U.D.C.A Act. & Div. Cient. 16(2): 519-523, Julio-Diciembre, 2013

RESUMEN

En la naturaleza es muy frecuente encontrar situaciones donde existen dos o más bandos que interactúan entre sí, de forma tal que uno hace el papel de cazador y el otro hace el de presa. A esta interacción entre especies se le denomina cacería. Existen múltiples modelos matemáticos que describen el comportamiento entre estas especies e, inclusive, considerando otras especies en la dinámica. Usualmente, la dirección del vector velocidad del cazador es igual a la dirección del vector velocidad de la presa, a velocidades que pueden ser constantes o no. Esta es la técnica usual de persecución, pero la principal desventaja es que la presa puede percibir cuando el cazador se aproxima a ella y, de esta forma, brindarle valiosos segundos de ventaja para huir, lo cual, es un problema, sobre todo, para aquellos cazadores que carecen de velocidad suficiente para atrapar una posible presa. En este documento, se describe una técnica especial de persecución que utiliza un elemento adicional, que se puede considerar como mimetismo, ya que la idea es engañar a la presa haciéndole creer, de alguna forma, que nunca existe acercamiento. En esta técnica, se desprecian efectos, como el cambio de tamaño del cazador, sombras, entre otros. Se deducen las ecuaciones de movimiento del camuflaje y se realizan simulaciones, en algunos momentos especiales, de estas ecuaciones. Estas ecuaciones son fáciles de simular y los resultados sugieren que, en algunos casos, esta estrategia es mejor que las técnicas clásicas de persecución.

Palabras clave: Ecuaciones diferenciales, persecución, mimetismo.

SUMMARY

In nature it is very common to find situations where two or more species interact in a specific way, being one the hunter and the other one the prey. This interaction between species is designated as hunting. There are many mathematical models that describe this behavior between species, considering even other species in the dynamics. Usually the direction of the hunters velocity vector equals the direction of the preys velocity vector, at speeds that may be or not constant. This is the usual technique of persecution. But the main disadvantage of this technique is that the prey can sense when the hunter approaches, which provides an advantage of valuable seconds to escape, which means a problem, especially for those hunters which do not develop adequate speed to catch the possible victim. This paper describes a special technique that uses an additional element, which can be considered as mimicry, since the idea is to fool the prey, to believe in some way that approach never occurs. In this technique effects such as change in the hunters size and shadows, between others are despised. Camouflage movement equations are deduced and in some special cases simulations of these equations are performed. These equations are easy to simulate and the results suggest that in some cases this strategy is better than the classical persecution techniques.

Key words: Differential equations, chase, mimicry.

INTRODUCCIÓN

La primera vez que fue descrito este tipo especial de movimiento fue en 1995, por Srinivasan & Davey. Este movimiento consiste en aproximarse, de manera sigilosa, a un objetivo predeterminado, sin que éste se percate del desplazamiento por parte del agresor. En esta persecución, el agresor se mueve, de forma tal, que su trayectoria depende de un punto fijo de referencia y la trayectoria del objetivo (Anderson & McOwan, 2003a). Los puntos de la trayectoria del agresor estarán ubicados en las líneas que unen el punto de referencia mencionado y los puntos de la trayectoria del objetivo, en un instante dado.

Para este movimiento, se deben despreciar efectos, como el tamaño, a medida que exista el desplazamiento, para que, de esta forma, el objetivo sea incapaz de percibir que el agresor se dirige hacia él y crea, de alguna forma, que éste siempre ha estado inmóvil en un punto inicial o que en una variante se mantenga camuflado, por un fondo de referencia determinado (Hartcup, 1979). En la investigación realizada por Mizutani et al. (2003), se muestran indicios que las libélulas utilizan esta técnica para combatir en disputas territoriales y, además en Anderson & McOwan (2003b), mediante algunos experimentos, se comprueba que los humanos también son susceptibles a este movimiento.

Se pretende realizar la simulación numérica de las ecuaciones de movimiento para estas persecuciones y, de esta forma, reproducir soluciones para una familia especial de ecuaciones. Srinivasan & Davey (1995) describen varios algoritmos que permiten simular persecuciones, utilizando mimetismo. En este documento, se realizará una breve descripción de esta técnica y la deducción de las ecuaciones de movimiento; también, se harán simulaciones comparando las trayectorias de movimiento en casos de persecución mimetizada y persecución clásica; esto se llevará a cabo para escenarios donde el agresor y el objetivo se mueven a velocidad constante y a velocidad variable. Se concluirá que a velocidad constante la persecución mimetizada es mejor para el agresor y se debe optar por este tipo de movimiento, caso opuesto para el movimiento, donde la velocidad no es constante, donde esta técnica no siempre es la más eficiente y como tal, se debe omitir para una posible persecución.

MATERIALES Y MÉTODOS

Para describir las ecuaciones de movimiento de persecución mimetizada, se considerará el caso de dos dimensiones. La descripción tridimensional, se obtiene de manera semejante. Así la posición del objetivo se puede describir como un punto en el plano . Este punto también se puede considerar de manera vectorial, como un vector posición (Bender, 1978).

La posición del objetivo cambia cuando el objetivo se mueve (Curio, 1976) y, de esta forma, se puede relacionar la posición del objetivo con el tiempo; así que se notará z(t) a la trayectoria del objetivo en un tiempo t, mientras que la trayectoria del agresor es notada por r(t). Otro elemento adicional a considerar, inicialmente, es el punto de referencia, para el cual, la persecución mimetizada va a realizarse; este punto de referencia siempre permanecerá fijo en este movimiento, por lo tanto, el vector posición no depende del tiempo y se notará como r₀. Se define como línea de restricción a la línea recta que une los puntos de la trayectoria del objetivo con el punto de referencia. Como se observa en la figura 1, la línea que une al objetivo y el punto estacionario es la línea de restricción que está dada por:

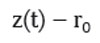
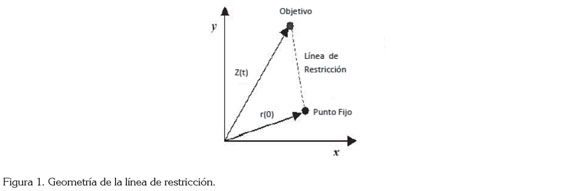
La condición de punto fijo puede ser elegida de diferentes formas, en particular si el agresor escoge en t = 0 el punto fijo como r₀, entonces r0= r₀. Una persecución mimetizada bajo estas condiciones, se puede observar en la figura 2.

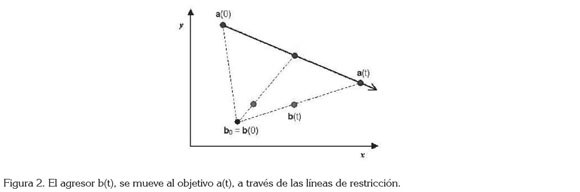
De esta forma, la ecuación de movimiento para el cazador en un tiempo t, debe satisfacer la ecuación:

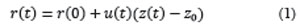
RESULTADOS Y DISCUSIÓN

Una condición adicional de consistencia es la siguiente:

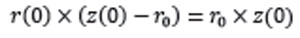
la cual, asegura que el agresor inicia en la línea de restricción. Para simplificar algunos cálculos, se va a suponer que r0= r₀. Esta suposición implicará que el agresor y el objetivo están en el mismo lugar en un tiempo T si u(T) =1. Tal tiempo, si existe, se denomina Tiempo de Captura. Algunos ejemplos de este tipo de persecución, se ilustran en la figura 3. En este ejemplo, se considera la función:

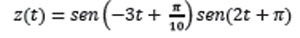
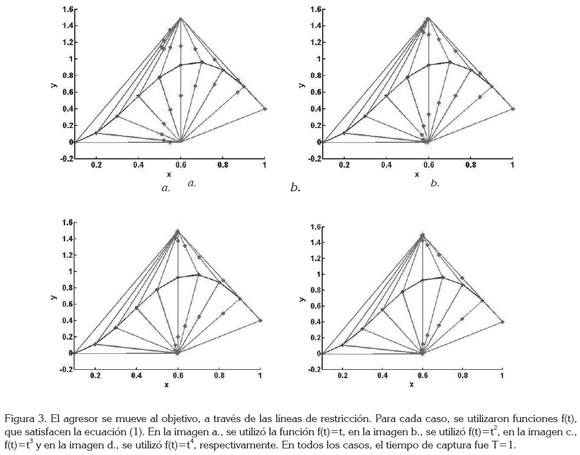
y dos puntos de referencia distintos: r0=(0,6;0) y r0=(0,6;1,5):.

Si u(t) puede ser encontrada, entonces la ecuación (1) tiene solución. Si el agresor y el objetivo se mueven con velocidad constante, entonces una única trayectoria óptima de ataque está determinada. Aunque también existe una solución que muestra un escape óptimo. Consideremos las magnitudes de la velocidad del agresor y el objetivo como y IzI=v y IrI=c.Derivando la ecuación (1) se obtiene:

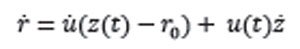
y, de esta forma, la velocidad desconocida se puede hallar tomando el cuadrado de la anterior expresión y calculando la norma; luego:

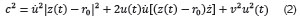
Esta es una ecuación cuadrática para u y usando la solución estándar para ecuaciones cuadráticas, concluimos para u:

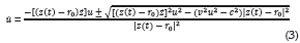
Con condición inicial u(0) =0. Como se observa para la ecuación (2) existen dos posibles soluciones de u: una positiva y una negativa. La solución negativa corresponde a una trayectoria de escape utilizando persecución mimetizada; aún no se ha encontrado en la naturaleza algún ser vivo que adopte está posición de escape para su beneficio (Glendinning, 2004).

La ecuación (3) muestra la proporción de avance ideal para un agresor que utilice la técnica de persecución mimetizada. Se puede mostrar que la ecuación (3) no tiene solución analítica (Murphy, 1960), por lo tanto, se utilizan métodos computacionales para visualizar soluciones de la misma.

En las técnicas clásicas de persecución, los agresores se mueven directamente hacia su presa, en cada instante (Alexander, 2003) y las ecuaciones que rigen este comportamiento ya han sido bien descritas por diferentes autores. Un modelo de persecución clásica, se discute en Davis (1962), en donde se atribuye el primer modelo matemático a Bouguer, en 1732.

En este caso, si el objetivo tiene una posición z(t) , entonces el agresor se mueve sobre la curva r(t) a cada instante, con dirección de la velocidad dada por la línea que une a r(t) y z(t). Si el agresor tiene velocidad constante c>0, entonces la ecuación diferencial del movimiento está dada por:

En general, las simulaciones numéricas sugieren que si el agresor se mueve más rápido que el objetivo y ambos (el objetivo y el agresor) tienen velocidad constante, entonces la técnica de persecución, utilizando mimetismo, es más efectiva que las técnicas clásicas de persecución (Glendinning, 2004). Por otra parte, si se realiza otra restricción a las velocidades, suponiendo que la velocidad del objetivo no es constante, las simulaciones numéricas sugieren que la persecución, utilizando mimetismo, no es la más efectiva en todos los casos como se ilustra en el ejemplo de la figura 4.

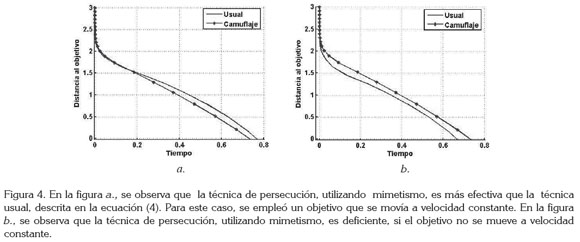
Mediante algunos juegos de computadora, se ha mostrado que los seres humanos también son susceptibles a este tipo de movimiento (Anderson & McOwan, 2003b); para ello, se utilizaron diferentes experimentos que involucran persecución usual y persecución utilizando mimetismo. En particular, este movimiento ha tenido especial interés por los científicos durante los últimos años, debido a las aplicaciones que han surgido de la misma técnica (Reddy et al. 2006). Además, si el objetivo se mueve a velocidad constante, las ecuaciones de persecución, utilizando mimetismo, no tienen soluciones cerradas, en términos de funciones conocidas (Murphy, 1960); asimismo, en estas situaciones, la persecución suele ser más eficiente que las técnicas clásicas de persecución (Glendinning, 2004). Para el trabajo posterior, se pueden formular una serie de preguntas como: ¿Es posible determinar una técnica mixta, de tal forma que se tomen los elementos a destacar entre la persecución utilizando mimetismo y las persecuciones tradicionales?, ¿existe en la naturaleza un servivo que utilice la técnica de persecución para escapar de un cazador? Es claro que esta técnica ofrece mucho por discutir y se ha convertido en una línea de investigación atractiva para las matemáticas aplicadas contemporáneas.

Conflicto de intereses: El manuscrito fue preparado y revisado con la participación de todos los autores, quienes declaramos que no existe ningún conflicto de intereses que ponga en riesgo la validez de los resultados presentados.

BIBLIOGRAFÍA

1. ALEXANDER, R.M. 2003. Principles of animal locomotion. Princeton University Press. 384p.

2. ANDERSON, A.J.; McOWAN, P.W. 2003a. Model of a predatory stealth behavior camouflaging motion. Proc. R. Soc. Lond. B 270:489-495.

3. ANDERSON, A.J.; McOWAN, P.W. 2003b. Humans deceived by predatory stealth strategy camouflaging motion. Proc. R. Soc. Lond. B. 270:S18-S20.

4. BENDER E. 1978. An introduction to mathematical modeling, A Willey Interscience Publication John Willey y Sons. 256p.

5. CURIO, E. 1976. The etiology of predation, Berlin: Springer- Verlag. 250p.

6. DAVIS, H. 1962. Introduction to Nonlinear Differential and Integral Equations. New York: Dover Publications. 559p.

7. GLENDINNING, P. 2004. The mathematics of motion camouflage, Proc. R. Soc. Lond. B 271:477-481.

8. HARTCUP, G. 1979. Camouflage: A history of concealment and deception in war. North Pomfrett, Vermont: David y Charles. 156p.

9. MIZUTANI, A.; CHAHL, J.; SRINIVASAN, M. 2003. Motion camouflage in dragonflies. Nature. 423:604.

10. MURPHY, G.M. 1960. Ordinary differential equations and their solutions. Princeton, NJ: Van Nostrand. 451p.

11. REDDY, P.V.; JUSTH, E.W; KRISHBAPRASAD, P. 2006. Motion camouflage in three dimensions. IEEE Conference on decision and control p.3327-3332.

12. SRINIVASAN, V.; DAVEY, M. 1995. Strategies for active camouflage of motion. Proc. R. Soc. Lond. B 259: 19-25.

Recibido: Noviembre 6 de 2012 Aceptado: Julio 11 de 2013