CIENCIAS SOCIALES Y ECONÓMICAS-Artículo de Reflexión

LA TRANSFERENCIA DEL APRENDIZAJE EN MATEMÁTICA: EL CASO DE LAS FUNCIONES LINEAL, CUADRÁTICA Y EXPONENCIAL

TRANSFER OF LEARNING IN MATHEMATICS: THE CASE OF LINEAR, CUADRATIC AND EXPONENTIAL FUNCTIONS

Alfonso Gómez¹, Yasmín Guzmán²

¹ Licenciado en Matemáticas, Doctor en Educación, Profesor Programa de Matemáticas Universidad de Cartagena, Cartagena, Colombia, agomezm1@unicartagena.edu.co

Rev. U.D.C.A Act. & Div. Cient. 16(2): 543-551, Julio-Diciembre, 2013

RESUMEN

La transferencia del aprendizaje es para algunos autores el propósito final de dicho proceso, ya que el individuo se educa para la vida y los conocimientos recibidos deben servirle para su desempeño. Siguiendo esta dirección, el presente trabajo muestra los resultados de la investigación realizada sobre la transferencia del aprendizaje, en tres temas de la enseñanza de la matemática, del programa de noveno grado, del nivel de media básica, a partir de los contenidos sobre definiciones y ejercicios presentados en los textos, utilizando el análisis de contenido de los libros, clasificándolos de acuerdo con las definiciones indicadas y con los ejercicios resueltos y propuestos y teniendo en cuenta el concepto clásico de transferencia de Perkins y Salomon, la transferencia en el aprendizaje de la matemática desarrollado por Santos y la transposición didáctica en los contenidos analizados, fenómeno inherente en la exposición de la temática expuesta en los textos escolares. En términos generales, los resultados mostraron que en los libros de textos, se presenta una transferencia cercana, quedando relegado el propósito de un aprendizaje útil para otras instancias.

Palabras clave: Enseñanza media, textos escolares, álgebra, problemas.

SUMMARY

Transfer of learning is for some authors the ultimate goal of this process, since individuals are being educated for life and the knowledge received must serve in their performance. Following this direction, this paper presents the results of a research conducted on the transfer of learning in three items of teaching mathematics in the ninth level of the basic teaching curriculum, based on definitions and proposed problems in the textbooks, applying content analysis of texts, taking into account the classical concept of transfer of Perkins and Solomon, the transfer of learning developed by Santos and the didactic transposition of contents, a phenomenon inherent in the statement of the issues presented in textbooks. Overall results showed that the transfer in textbooks is lowroad, relegating the purpose of a useful learning in other instances.

Key words: Secondary education, textbooks, algebra, problems.

INTRODUCCIÓN

El problema de la transferencia: En el programa de matemática de noveno grado del bachillerato colombiano, se estudia una parte del álgebra clásica elemental y en la temática, se tratan las funciones lineales, cuadráticas y exponenciales. Una primera mirada del contenido de los textos escolares muestra que la exposición hace énfasis en la matemática instrumental o, lo que es lo mismo, en la parte operativa, situación que conlleva a analizar con más detalle de qué manera se da el proceso de transferencia, cuando se desarrollan los ejemplos, ya sea para el aprendizaje de conceptos, para su aplicación o para su uso en la vida diaria.

Para llevar a cabo los procesos de enseñanza y aprendizaje, de manera completa, es indispensable que el estudiante sea capaz de utilizar lo aprendido en ciertas situaciones específicas fuera del ambiente escolar, por lo que es necesario empezar con la apropiación de conceptos, para así lograr aplicarlo a situaciones múltiples. En este punto, el docente debe valorar la importancia de la aplicación de conceptos dentro de la matemática, a partir de los textos de estudio, como medio estratégico, para el logro de la transferencia del aprendizaje, lo cual, implica que es importante hacer una revisión de éstos, para determinar qué tipo de transferencia de aprendizaje se promueve con ellos y hasta qué punto estos textos constituyen un factor propiciador de la transferencia.

La noción de transferencia del aprendizaje fue introducida en la primera década del siglo XX, por Edward Thorndike y Roberto S. Woodworth, en 1901, como transferencia de la práctica (Gómez, 2005), al explorar en los individuos cómo transferían el aprendizaje de un contexto a otro. Su teoría implica que la transferencia del aprendizaje dependa de la proporción de similaridad entre la tarea de aprendizaje y la tarea de transferencia de ese aprendizaje, es decir, la transferencia del aprendizaje depende de la presencia de elementos muy demarcados en las situaciones nuevas y originales de aprendizaje, lo cual, lleva a suponer que la transferencia es siempre específica y no general.

En términos generales, la transferencia del aprendizaje es el proceso, mediante, el cual, el individuo es capaz de trasladar o traspasar los conocimientos adquiridos, previamente, en conceptos, en operaciones, en estrategias, en actitudes, en habilidades, en principios y en destrezas, para enfrentarlos a nuevas situaciones, ya sean del mismo contexto escolar o de la vida diaria (Ruiz, 2002).

Wenzelburger (1987) afirma que la transferencia del aprendizaje ocurre cuando lo que se aprende en una situación facilita o inhibe el aprendizaje o desempeño en otras situaciones; además, manifiesta que si se descarta la transferencia no se justificaría la enseñanza ni la existencia de las instituciones educativas, por eso el término transferencia es tan importante en educación; de allí es significativo resaltar que es transferible todo lo que se aprende, como habilidades psicomotrices, habilidades cognoscitivas y actitudes afectivas (Gómez, 2005).

Perkins & Salomon (1992) consideran que la transferencia del aprendizaje ocurre cuando lo aprendido en un contexto o conjunto de materiales impactan en el desempeño en otro contexto o con otros materiales relacionados, es decir, la conexión o relación que existe entre lo que se aprende o lo que se sabe con otras experiencias y contextos. También piensan que uno de los objetivos de la educación es lograr aplicar o transferir las habilidades y los conceptos que se han aprendido en clase con otras áreas, temáticas o sucesos de la vida diaria, que, por lo general, no siempre ocurre, pues no tienden a realizar dichas conexiones con otros contextos de aprendizaje; por consiguiente, la instrucción debe estar dirigida para realizar la transferencia, de ahí que se debe mirar como un proceso flexible que ayuda al estudiante a asegurar el conocimiento, en diferentes situaciones.

Bransford et al. (2000) proponen que la transferencia del aprendizaje depende de varios factores, entre los cuales, se destacan:

a. La necesidad del aprendizaje previo. El sujeto debe lograr un aprendizaje inicial, de apertura, que sea suficiente como para brindar soporte a la transferencia, pero toma tiempo aprender una disciplina compleja. Por ello, en la verificación de la transferencia, se debe tomar en cuenta el grado en que el aprendizaje original fue comprendido.

b. La inversión de tiempo en la tarea. El tiempo que se dedica a la tarea, por sí mismo, no es garantía de un aprendizaje sólido y con un alto potencial de transferencia; lo más importante es cómo la gente usa su tiempo mientras aprende. Conceptos tales como el de ''práctica deliberada'', enfatizan la importancia de ayudar a los estudiantes a monitorear su aprendizaje, buscar la realimentación sobre su desempeño, supervisar la eficiencia de las estrategias empleadas y evaluar el proceso y nivel de comprensión obtenido.

c. La necesidad de la comprensión en el aprendizaje. El aprendizaje con alto grado de comprensión tiene mayor probabilidad de facilitar la transferencia que el aprendizaje, mediado por la memorización de información textual.

d. La variación del contexto de aprendizaje. El aprendizaje, que es promovido en una variedad de contextos, tiene mayor probabilidad de ser transferido a nuevas situaciones que aquel obtenido en un único contexto. Cuando el material aprendido es multicontextualizado, el sujeto tiene mayor oportunidad de extraer rasgos relevantes de los conceptos y desarrollar una representación más flexible del conocimiento, lo cual, favorece un mayor grado de generalización.

e. La comprensión flexible del estudiante. El sujeto desarrolla una mayor flexibilidad en la comprensión acerca del cuándo, dónde, por qué y cómo usar el conocimiento para resolver nuevos problemas, si aprende cómo extraer las ideas y los principios subyacentes de sus ejercicios de práctica en el aprendizaje.

f. La evaluación de la transferencia. La transferencia del aprendizaje es un proceso activo y continuo, por tanto, no debería ser evaluado puntualmente con un test de transferencia; para tal fin, se debería considerar cómo el aprendizaje previo afecta los aprendizajes posteriores bajo condiciones reales de las tareas, tal como el aumento de la velocidad o medida del progreso en el aprendizaje, en un nuevo dominio.

g. La importancia de la experiencia previa. Todo aprendizaje supone la transferencia de experiencias previas, inclusive, en los casos de aprendizaje inicial; no obstante, ella no ocurre de manera espontánea ni es siempre evidente. De allí, que un docente efectivo intente inducir la transferencia positiva mediante la identificación activa de las fortalezas que el estudiante trae a la situación de aprendizaje, extendiendo puentes entre el conocimiento del alumno y el aprendizaje de los objetivos instruccionales previstos.

h. La necesidad de evitar la transferencia negativa. Algunas veces el conocimiento que la gente trae a una nueva situación le impide obtener subsecuentes aprendizajes, porque guía el pensamiento en una dirección equivocada (Brandsford et al. 2000). En tales casos, el docente debe ayudar al estudiante a cambiar su concepción original antes de utilizar las concepciones erradas, como base para comprensiones adicionales futuras.

De lo anterior, se puede resaltar lo importante que es utilizar la transferencia en las diferentes áreas del conocimiento, como medio de interacción en el aprendizaje ocurrido en una situación, ya sea dentro de la misma área o diferentes. De allí, que el docente debe utilizar la transferencia como herramienta, para que el estudiante mejore su desempeño académico.

Al hablar de transferencia, se distinguen varios tipos de ella, siendo los más comunes la transferencia positiva, la transferencia negativa, la transferencia cercana y la transferencia lejana (Perkins & Salomon, 1992). La transferencia positiva, se define como un proceso, en el que el aprendizaje en un contexto mejora el desempeño en otro contexto; por ejemplo, quien habla un idioma encuentra más fácil aprender el idioma relacionado con el primero. La transferencia negativa, se refiere al proceso por medio, del cual, el aprendizaje en un contexto impacta negativamente en otro contexto, es decir, cuando el aprendizaje de una tarea interfiere en el aprendizaje de una segunda. Por otra parte, cuando se transfieren contenidos a situaciones o contextos muy similares, se trata de una transferencia cercana, pero si se trasladan aprendizajes a contextos remotos y aparentemente ajenos, se trata de una transferencia lejana.

Otra clasificación de los tipos de transferencia, se debe a Gagné (1970), quien identifica dos tipos de transferencia: lateral y vertical. La transferencia lateral, se refiere al aprendizaje adquirido previamente y su utilización en la nueva tarea, sobre el cual, se realizará la transferencia, en otras palabras, el aprendizaje anterior es fundamental para el aprendizaje posterior; por ejemplo, el conocimiento previo que debe tener un estudiante de secundaria para graficar funciones lineales, cuadráticas o exponenciales.

Por otra parte, la transferencia vertical tiene lugar cuando el conocimiento previamente adquirido permite comprender una nueva tarea de la misma naturaleza o nivel de complejidad más alto; por ejemplo, la aplicación de las operaciones realizadas con funciones, de allí que es en este espacio donde empieza a tener importancia la transferencia al volverse significativo el aprendizaje, pues el estudiante es capaz de reinventar o ampliar su horizonte cognitivo.

MATERIALES Y MÉTODOS

El trabajo, se desarrolló en torno al concepto clásico de transferencia de Perkins & Salomon (1992). La información recolectada, se obtuvo de los textos Matemática en Acción 4, de Losada et al. (1978), Espiral 9, de Moreno (2005) y Glifos Procesos Matemáticos 9, de Arévalo et al. (2008). La escogencia de los textos obedeció a dos hechos importantes. En primer lugar, se tuvo en cuenta la fecha de publicación, de acuerdo con la aparición de los lineamientos curriculares: antes de los lineamientos, durante los lineamientos y después de los lineamientos. En segundo lugar, los textos fueron los más utilizados en el medio donde se desarrolló el trabajo investigativo, debido al prestigio de los autores y las editoriales.

Los libros examinados, se clasificaron en tres clases o categorías, según la forma como se presenta el contenido, de acuerdo con González & Sierra (2004): expositivo, tecnológico y comprensivo. Expositivo, cuando los temas matemáticos se presentan como enunciados, reglas y procedimientos aparentemente aislados y sin conexión a la realidad, pero obedece en cierta forma a alguna presentación de la matemática; tecnológicos, cuando la presentación de los conceptos inducen la mecanización, siguiendo un estilo conductista, con la intensión de adquirir destrezas sobre ciertos procesos, mediante la ejercitación y, comprensivo, cuando la exposición de los conceptos obedece a una construcción formal o axiomática, con cierto grado de rigor de la matemática, por la forma concatenada como aparecen los conceptos (Gómez-Granell, 1989), estableciendo una relación adecuada de los conceptos estudiados con otros conceptos previos.

Para el examen de las definiciones y de los ejercicios, se hizo un análisis exhaustivo, teniendo en cuenta la idea de Monterrubio & Ortega (2011), que consiste en detallar los contenidos analizados en lo relacionado con las definiciones, según su presentación como teoría axiomática, la secuenciación y la organización en el contexto, las conexiones con los conceptos que le preceden y los conceptos siguientes y las actividades o problemas, que tienen por objeto la obtención de la transferencia.

En términos generales, al examinar definiciones y ejercicios, según Gómez (1997), se considera como sinónimos las expresiones textos escolares, textos guías, textos de estudio y manuales escolares, los cuales, se caracterizan por ser libros impresos, producidos por las editoriales con más alto nivel de ventas y que se utilizan en la escuela, para la comunicación de los conocimientos. Estos textos tienen en común que ellos obedecen a las políticas de Estado, con base a las políticas curriculares y que han sido impresos con ánimo educativo y a nivel comercial.

Para la realización del trabajo, se estudiaron los tipos de transferencias cercana y lejana en el aprendizaje; luego, mediante el examen de tres textos de matemática de noveno grado, se analizó cómo se suscita la transferencia, a través de los ejercicios resueltos y planteados, en el sentido de ayudar a resolver situaciones del diario vivir; para ello, se utilizó una metodología descriptiva-comparativa y cualitativa, ubicando los textos de matemática de 9° de educación básica secundaria en dos épocas: antes y después de los lineamientos curriculares, según las técnicas propuestas por González & Sierra (2004). El análisis de los contenidos, se realizó según la dimensión pragmática aplicada a manuales escolares, presentada por Monterrubio & Ortega (2011); luego, se llevó a cabo una comparación de los temas bajo estudio, confeccionando cuadros comparativos con los datos fundamentales teoría y ejercicios de los textos. Los contenidos de los ejercicios de los textos, se analizaron, ajustados al concepto clásico de transferencia, dado por Perkins & Salomon (1992), mediante el análisis conceptual en la presentación de los contenidos, el análisis didáctico cognitivo, desde el efecto producido por la transposición didáctica y el análisis fenomenológico, aplicado a la organización de los conceptos, apoyados en el estudio documental.

RESULTADOS Y DISCUSIÓN

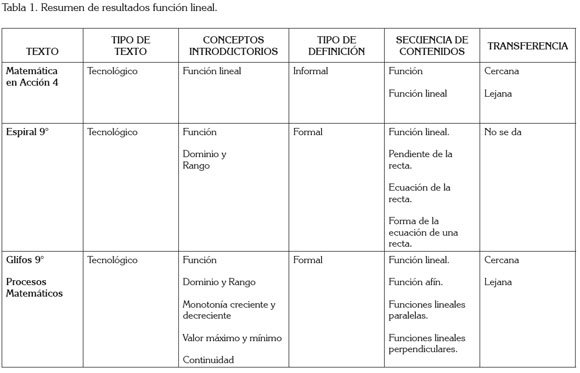
Al hacer un análisis de las definiciones, los ejemplos y los ejercicios propuestos, se encontró que los textos, bajo estudio, se ciñen a los programas curriculares, propuestos por el Ministerio de Educación Nacional, atendiendo a los lineamientos curriculares, de acuerdo con la fecha de publicación del texto. Al realizar el análisis de contenidos, la parte conceptual correspondiente a todos los temas y en todos los textos analizados, se desarrolla en un ambiente tecnológico y expositivo, pero no comprensivo, porque el tratamiento no es estrictamente axiomático; todas las definiciones son formales, aunque no exactamente rigurosas, excepto en el texto Matemáticas en Acción, para la función lineal. La secuencia de contenidos sigue el orden de complejidad función lineal, función cuadrática y función exponencial, en todos los textos; el concepto de función es un concepto introductorio, ya sea en el mismo texto o en el texto precedente de la colección; el tipo de transferencia para la función lineal es cercana, excepto en texto Espiral 9°, donde no se da; finalmente, para la función exponencial, la transferencia se aproxima a la cercana lateral y algo de transferencia vertical (Gómez, 2005), en el texto Espiral 9° (Moreno, 2005). De acuerdo con Chevallard (2000) y Solarte (2006), el texto Matemáticas en Acción hace la transposición didáctica del concepto de función, de cierto modo fundada en el concepto de ecuación, produciéndose lo que se llama la desincretización del saber, tratando de conseguir un efecto de simplificación (D'Amore, 2006), es decir, un puente de comunicación entre el docente y el estudiante, respecto al saber a enseñar. Este hecho es recurrente en los ejercicios propuestos, donde se debería decir que la ecuación representa una función, dándose la desincretización del saber en el sentido de no avanzar al no poderse asimilar la diferencia entre ecuación y función. La presentación del concepto en el texto comienza formal, pero se vuelve informal, mediante los ejemplos; pues el objetivo es conectar los conceptos de función lineal y ecuación lineal.

En términos generales, se puede establecer que la introducción del concepto es formal; algunos conceptos en el texto no corresponde al programa curricular del grado, como lo es la continuidad de una función definida en Glifos 9 (Arévalo et al. 2008); tanto los ejercicios propuestos como los ejemplos conducen a un aprendizaje mecánico, lo cual, permite clasificarlo como un texto tecnológico; además, los problemas propuestos, en cierta manera, llevan a una transferencia cercana y lateral, pero inmediata, vislumbrándose cierto tipo de transferencia lejana en algunos problemas propuestos. La tabla 1 resume los resultados encontrados.

Para la función cuadrática, la transferencia es cercana lateral, porque los ejercicios se reducen a hallar la función bajo condiciones inherentes, excepto en el texto Matemáticas en Acción 4 (Losada et al. 1978), donde está ausente. En lo relacionado con la exposición de algunos ejercicios, no se presenta total claridad en los enunciados, se confunden las expresiones función, polinomio, ecuación y fórmula; se muestran ejercicios de funciones con dos variables al tratar de expresar el área A y el perímetro P de un campo rectangular en función de su largo x y su ancho z (Moreno, 2005); la recta y la parábola, se presentan algunas veces como lugares geométricos y, otras, como funciones en Moreno (2005).

En el texto Matemática en Acción 4 (Losada et al. 1978), es poca la información que se encuentra sobre las funciones cuadráticas, su definición es formal, los ejercicios propuestos y resueltos no llevan a establecer ningún tipo de transferencia, al igual que en las funciones lineales; el texto se remite al volumen anterior, como base, Matemática en Acción 3, de los mismos autores.

Espiral 9° (Moreno, 2005) introduce el concepto de función cuadrática de manera formal, aunque se tiene que x es la variable independiente y en su definición no aparece; el dominio está implícito, al decir que x puede tomar cualquier valor real, pero su rango no está definido; se debe aclarar que su gráfica es una parábola, pero no toda parábola representa una función cuadrática.

Al analizar Espiral 9° (Moreno, 2005) es importante destacar, según Bransford et al. (2000), la importancia del aprendizaje previo y la necesidad de evitar la transferencia negativa; en este sentido, el texto propone unas actividades de preparación o iniciales, en que el docente debe verificar la comprensión del aprendizaje anterior y, si es necesario, modificar conceptos que trae el estudiante, que más adelante conduciría a una transferencia negativa.

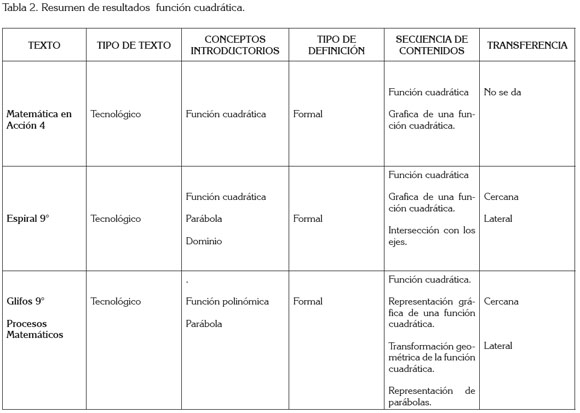
Adicionalmente, Aréchiga (1998) propone que el aprendizaje de las matemáticas se debe dar en tres etapas. La primera, abarca los conceptos matemáticos y la forma como están organizados, para luego comunicarlos; el texto bajo análisis, ubica el concepto de función cuadrática en el programa correspondiente del curso, ilustrándolo con algunos gráficos y ejemplos, que conducen a generalizaciones y así se presenta la segunda etapa, los que más tarde son utilizadas por los estudiantes en la solución de situaciones problema dentro de la misma matemática o en otras disciplinas, asumiéndose finalmente, la tercera etapa. Según esto, el texto propicia la transferencia cercana y lateral, a través de sus problemas dentro de la misma matemática y su relación con otras áreas, como la física. La transferencia lejana está ausente en los textos analizados, muy a pesar que la función cuadrática es fuente de un gran número de aplicaciones. Se resume el análisis de resultados en la tabla 2.

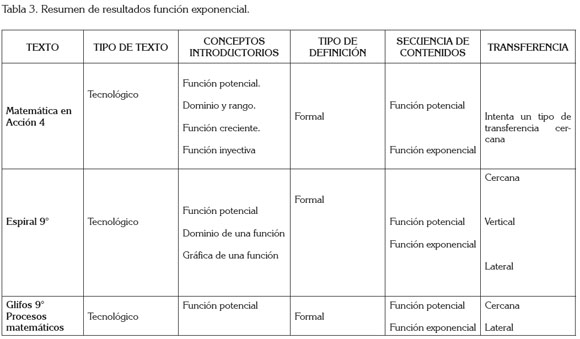
Respecto a la función exponencial, los textos toman como punto de partida el concepto de función potencial con exponente racional; presentan el concepto de función exponencial formal, pero incompleto; se puede apreciar algunas propiedades de las potencias que son de mucha ayuda para graficar; el dominio de la función es implícito al escribir que x es un número real; no se especifica su recorrido al inicio, pero cuando toman sus propiedades al expresar que la función exponencial es siempre de valor positivo, queda implícito el rango; consideran la propiedad de que la función es creciente y biyectiva, pero no consideran el caso cuando la función es decreciente, es decir, no se considera el caso de que y = a^-x también es una función exponencial, excepto en Espiral 9° (Moreno, 2005), donde se exponen algunos ejemplos. La secuencia, el contenido y la ubicación de los temas desarrollados están acordes con los programas curriculares. De las situaciones problemas que se analizan, se encuentra una pequeña discontinuidad en la secuencia de los contenidos, pues la solución requiere de funciones exponenciales de base natural, hecho que no está claro en ninguno de los textos. La transferencia presente en los textos es de tipo lateral y vertical, con una aproximación a la transferencia lejana, mediante el tratamiento de algunos ejemplos relacionados con el problema de interés compuesto, crecimiento de bacterias. La tabla 3 muestra una síntesis del análisis.

A manera de cierre, se pueden derivar algunas conclusiones, las cuales, se agrupan teniendo en cuenta el papel que juegan los contenidos en el aprendizaje de las matemáticas, la presentación de los mismos y el logro de la transferencia.

El contenido de los libros de textos y la organización de los temas, en algunos casos, no están acorde al programa, según el grado; estos siguen la estructura de los lineamientos curriculares propuestos por el gobierno, pero no obedecen a las necesidades del estudiante y al contexto donde se desenvuelve, al transponer los conceptos en los textos, para facilitar el aprendizaje de los mismos; lo que se hace es restarle su verdadera esencia para su utilización, convirtiéndose en un obstáculo para su formación, pues un verdadero aprendizaje debe estar basado en un buen manejo conceptual, que, en ocasiones, aparecen definiciones auxiliares, que terminan desorientando al estudiante.

Ante las falencias descubiertas es obligatorio que el docente analice cada texto de trabajo y verifique su contenido de enseñanza, valiéndose de sus conocimientos y experiencia, a fin de enriquecer su quehacer e implementar, en la planeación curricular, actividades o tareas de aprendizaje, que articulen ejercicios y prácticas, para que el estudiante logre realizar conexiones y aplicar nuevos aprendizajes o habilidades.

El aspecto instrumental de las matemáticas que incita a la ejercitación de un concepto desde la metodología conductista, pero con muy pocas excepciones, llevan al estudiante a hacer un análisis del concepto, sus propiedades, la relación con otros conceptos y con otras áreas del saber. En síntesis, los ejemplos resueltos y los ejercicios propuestos pretenden ilustrar el concepto, dejando al estudiante, por lo general, sin acceso a identificar la estructura profunda de los problemas en la etapa final del análisis de resultados (Santos, 1997).

A lo largo del trabajo, se ha entendido la transferencia no como aplicación de concepto sino como el traspaso de los conocimientos a otras esferas; se observa que si hay algo de transferencia es de tipo lateral y cercana, pero hay ausencia de transferencia lejana. De otra parte, según la metodología propuesta en el trabajo, se observó que los textos se desarrollan en un ambiente tecnológico y expositivo, pero no comprensivo, hecho que deja un aprendizaje incompleto, pues el proceso de aprendizaje, en este caso, culmina con la transferencia lejana.

También es pertinente manifestar que los conocimientos adquiridos en la escuela deben ser útiles dentro y fuera de las instituciones educativas; una de las áreas más importantes y propiciadora para esto es la matemática; sin embargo y, por lo general, no ocurre, pues su enseñanza, en ocasiones, está limitada a la mecanización y a la memorización de ejercicios; es por ello, que la instrucción debe estar dirigida a realizar la transferencia, es decir, a que el estudiante sea capaz de traspasar las habilidades y los conceptos que han aprendido en clase a otras áreas o tópicos y a los acontecimientos de su diario vivir. En este proceso, el docente debe favorecer una serie de actividades, ejercicios y prácticas, para que los estudiantes realicen este tipo de conexiones, tener claridad sobre las metas y los propósitos de transferencia y el impacto que tiene en la comprensión de los contenidos de enseñanza, con el fin que el estudiante comprenda el propósito de hacer conexiones y comience a encontrar los diversos contextos, para realizar la transferencia.

Finalmente, se debe señalar que este trabajo es apenas una aproximación al problema de la transferencia del aprendizaje, en tres temas específicos. Sería provechoso extender esta investigación, analizando cómo se dará la transferencia a la luz de los lineamientos curriculares y los estándares sobre matemática en la enseñanza en el nivel de básica, comparando lo que aquí se presenta con lo que ocurre en otros países, como Venezuela, Perú, Costa Rica y México (Santos, 1997).

De acuerdo con lo expresado inicialmente, se reafirma la presentación de los contenidos en forma instrumental, estimulando a la ejercitación de un concepto de tipo conductista, sin llevar al estudiante a hacer un análisis del concepto, sus propiedades, la relación con otros conceptos y con otras áreas del saber, excepto en los casos donde se intenta, con algunos ejercicios, la transferencia de tipo vertical. Los ejemplos resueltos y los ejercicios propuestos pretenden ilustrar el concepto, resaltando sus características, entendiéndose la transferencia, en este caso, como ampliación del concepto, en términos de una transferencia lateral.

En términos generales, la presentación de ejercicios resueltos y problemas propuestos deja al proceso de aprendizaje incompleto, pues no se vislumbra la utilidad de los conocimientos en ausencia de la transferencia lejana, entendiendo ésta como el traspaso de los conocimientos a otras esferas, donde el conocimiento se hace explícito y como lo afirma Pozo (2006), cuando un conocimiento se hace explícito surge un tipo de conocimiento declarativo, que produce la adquisición de hechos y sucesos, que tienen definición en el contexto cultural del estudiante y lo posibilita para generar aprendizajes significativos, que se pueden transferir, de manera adecuada, en otros contextos. Sobre este particular, Sanjosé et al. (2007), investigando sobre la transferencia en solución de problemas, conceptúa que para conseguir la transferencia es necesario la comprensión y la aplicación de los contenidos y así, de esta manera, los estudiantes saben lo que hacen. Las ideas expresadas acentúan la importancia de los ejercicios del texto escolar.

Conflicto de intereses: El manuscrito fue preparado y revisado con la participación de los autores, quienes declaramos que no existe ningún conflicto de intereses, que ponga en riesgo la validez de los resultados presentados.

BIBLIOGRAFÍA

1. ARÉCHIGA, J. 1998. Problemas de la transferencia de las matemáticas. Revista Academia. (México), 4(1): 30-32. Disponible desde internet en: http://www. scribd.com/doc/32358041/Academia-4 (con acceso 08/08/2006).

2. ARÉVALO, S.; GARZÓN, L.; PERAFÁN, B.; RANGEL, J.; CHÁVEZ, S.; SILVA, O.; RODRÍGUEZ, J.; DÍAZ, R.; JIMÉNEZ, J.; LÓPEZ, M. 2008. Glifos, Procesos matemáticos 9°. Ed. Libros & Libros S.A. (Bogotá). 336p.

3. BRANSFORD, J.; BROWN, A.; COCKING, R. 2000. How people learn: Brain, mind, experience and school. Ed. National Academy Press. (Washington). 384p.

4. CHEVALLARD, Y. 2000. La Transposición Didáctica, del saber sabio al saber enseñado (3ª ed.). Ed. Aiqué. (Buenos Aires). 196p.

5. D'AMORE, B. 2006. Didáctica de la matemática. Ed. Magisterio (Bogotá). 470p.

6. GAGNÉ, R. 1970. The conditions of learning. Ed. Holt Rinehart and Winston (New York). 407p.

7. GÓMEZ, B. 1997. Los libros de textos de matemáticas. En: Sierra, M; Rico, L; Gómez, B. (eds). Las matemáticas del siglo XX Vol. 2. Ed. Fundación G. S. Ruipérez. (España). p.77-80.

8. GÓMEZ, M. 2005. La Transposición didáctica: historia de un concepto. Rev. Latinoam. Est. Educ. (México). 1(1):83-115.

9. GÓMEZ-GRANELL, C. 1989. La adquisición del lenguaje matemático: un difícil equilibrio entre el rigor y el significado. Rev. Com., Lenguaje y Educ. (España). 3(4):5-15.

10. GONZÁLEZ, M.; SIERRA, M. 2004. Metodología de análisis de libros de textos de matemáticas. Puntos críticos en la enseñanza secundaria en España durante el siglo XX. Enseñanza Cienc. (España). 22(3):389-408.

11. LOSADA, R.; DE LOSADA, M.; MATEUS, H. 1978. Matemática en Acción 4. Ed. McGraw-Hill Latinoamericana S.A. (Bogotá). 156p.

12. MONTERRUBIO, M.; ORTEGA, T. 2011. Diseño y aplicación de instrumentos de análisis y valoración de textos escolares de matemáticas. Rev. PNA. (España). 5(3):105-127.

13. MORENO, V. 2005. Espiral 9°. Ed. Norma S.A. (Bogotá). 356p.

14. PERKINS, D.; SALOMON, G. 1992. Transfer of learning. En: International Encyclopedia of Education. Ed. Pergamon Press. (Oxford). Disponible desde Internet en: http://learnweb.harvard.edu/alps/thinking/docs/traencyn.htm (con acceso 31/03/2011).

15. POZO, J. 2006. Adquisición de conocimiento. Ed. Morata. (España). 269p.

16. RUIZ, C. 2002. Mediación de estrategias metacognitivas en tareas divergentes y transferencia reciproca. Rev. Invest. Postgrado. (Venezuela). 17(2):1-10.

17. SANJOSÉ, V.; VALENZUELA, T.; FORTES, M.; SOLAZ- PORTOLÉS, J. 2007. Dificultades algebraicas en la resolución de problemas por transferencia. Rev. Electr. Enseñ. Ciencias. (España). 6(1):538-561.

18. SANTOS, L. 1997. La transferencia del conocimiento y la formulación o rediseño de problemas en el aprendizaje de las matemáticas. Rev. Méx. Invest. Educ. 2(3):11-30.

19. SOLARTE, M. 2006. Los conceptos científicos presentados en los textos escolares: son consecuencias de la transposición didáctica. Rev. Electr. Red Invest. Educ. (México). 1(4):1-12.

20. WENZELBURGER, E. 1987. La transferencia en el aprendizaje. Publicaciones de la asociación nacional e instituciones de educación superior. Versión electrónica 61. Disponible desde Internet en: http://201.161.2.34/servicios/p_anuies/publicacio - nes/revsup/res061/txt4.htm (con acceso 5/05/2007).

Recibido: Noviembre 22 de 2012 Aceptado: Octubre 2 de 2013