CIENCIAS DE LA SALUD-Artículo Científico

SIMULACIÓN DE RUTAS DE ALTERACIÓN DE CÉLULAS DE CUELLO UTERINO DESDE EL ESTADO NORMAL HASTA LESIÓN INTRAEPITELIAL DE BAJO GRADO

SIMULATION OF DISTURBANCE PATHS OF CERVIX UTERI CELLS FROM NORMAL STATE TO LOW GRADE SQUAMOUS INTRAEPITHELIAL LESION

Javier Rodríguez¹,Signed Prieto², Martha Melo³, Darío Domínguez⁴, Diana Cardona⁵, Catalina Correa⁶, Fredy López⁷, Ligia Victoria Rodríguez ⁸

¹ MD. Director del Grupo Insight. Director de la Línea de Profundización e Internado Especial: Física y Matemáticas Aplicadas a la Medicina, Universidad Militar Nueva Granada Centro de Investigaciones de la Clínica del Country, Carrera 79B No. 51-16sur Int. 5, Apto. 102, Bogotá, Colombia, e-mail: grupoinsight2025@yahoo.es

² Investigadora Grupo Insight. Universidad Militar Nueva Granada Centro de Investigaciones de la Clínica del Country, Carrera 79B No. 51-16sur Int. 5, Apto. 102, Bogotá, Colombia, e-mail: grupoinsight2025@yahoo.es

³ Matemática. Investigadora Grupo FRACUMNG. Facultad de Ciencias Básicas y Aplicadas. Universidad Militar Nueva Granada. Vereda Canelón, Condominio Palo E Teka, casa 23, Municipio de Cajicá, Cundinamarca, e-mail: martha.melo@unimilitar.edu.co

⁴ Matemático. Magister en Ciencias Económicas. Director Grupo de Investigación FRACUMNG. Facultad de Ciencias Básicas y Aplicadas, Universidad Militar Nueva Granada, Carrera 53 A No. 127-70, Apto. 1219, Bogotá, Colombia, e-mail: dario.dominguez@unimilitar.edu.co

⁵Investigadora Grupo Insight. Universidad Militar Nueva Granada Centro de Investigaciones de la Clínica del Country, Calle 54 C sur No. 87-21 Casa 111, Bogotá, Colombia, e-mail: margarita.cardona@annardx.com

⁶ Psicóloga. Investigadora Grupo Insight. Universidad Militar Nueva Granada Centro de Investigaciones de la Clínica del Country, Calle 45 sur No. 78i-25, Bogotá, Colombia, e-mail:scatalinacorreah@hotmail.com

⁷ Ingeniero de Sistemas, investigador Grupo Insight. Universidad Militar Nueva Granada Centro de Investigaciones de la Clínica del Country, Calle 23 No 68-59 Int. 10, Apto. 402, Bogotá, Colombia, e-mail: flogarcdos@gmail.com

⁸ Abogada. Investigadora Grupo Insight, Calle 147 No. 19-51 Torre 4 Apto. 104, Bogotá, Colombia, e-mail: ligiav_05@hotmail.com.

Rev. U.D.C.A Act. & Div. Cient. 17(1): 5-12, Enero-Junio, 2014

RESUMEN

Se desarrolló previamente un diagnóstico matemático de células halladas en la citología cervicovaginal, estableciendo caracterizaciones objetivas y reproducibles para los diferentes estadios de la alteración celular, desde normalidad hasta carcinoma. En este trabajo, se partió de dicha metodología, para establecer posibles rutas de alteración preneoplásica, desde normalidad hasta LEIBG. Se estudiaron diez imágenes digitales de células escamosas de cuello uterino, con diagnóstico normal. Las imágenes fueron analizadas mediante un software, con el que se calculó la dimensión fractal de los objetos matemáticos definidos. Se calcularon los valores de variabilidad fractal y AMI (Armonía Matemática Intrínseca) celular para cada muestra y, a partir de estos valores, se realizaron simulaciones de las rutas de alteración de cada célula normal hacia una célula LEIBG (Lesión Escamosa Intraepitelial de Bajo Grado), realizando tres posibles variacio nes de los espacios de ocupación celular en el espacio de Box-Counting. Cada ruta de alteración celular está definida por tres posibilidades de variación de ocupación espacial de los objetos celulares definidos. Cada una de estas posibilidades puede presentar características matemáticas de estados intermedios de la alteración. Los valores de la dimensiones fractales de los tres objetos definidos en las células normales: citoplasma, núcleo y totalidad, se hallaron entre 1,0512 y 1,9944 y los valores de variabilidad y AMI, entre 0 y 6. Se evidenció una organización fractal de la estructura celular cervical, que permite establecer simulaciones de su alteración, lo que representa una herramienta de utilidad en la práctica clínica.

Palabras clave: Dimensión fractal, Cáncer de cuello uterino, Citología, simulación, LEIBG.

SUMMARY

A mathematical diagnosis of cells from cervicovaginal cytology was previously developed establishing objective and reproducible characterizations for different stages of cellular disturbance from normality to carcinoma. In this paper we start from this methodology to establish possible routes of preneoplastic alteration from normal to L-SIL. Ten digital images of squamous cells of cervix uterine with normal diagnosis were studied. The images were analyzed through a software with which fractal dimension of defined mathematical objects was calculated. Fractal variability and Cellular Intrinsic Mathematical Harmony (IMH) values were calculated for each sample. From these values, simulations of disturbances paths of each normal cell towards to L-SIL cell were realized, doing three possible variations of spaces of cellular occupation in Box-counting space. A possible disturbance path towards to L-SIL state for each normal cell was established. Each path is defined by three variation possibilities of spaces of occupation of defined objects. Each possibility can exhibit mathematical characteristics of intermediate states of disturbance. Fractal dimension values of the three defined objects in normal cells: cytoplasm, nucleus and totality were between 1.0512 y 1.9944. Variability and IMH values were between 0 and 6. A fractal organization of cervix cellular structure was evidenced allowing to establish simulation of disturbance. This finding can represent a useful tool in clinical practice.

Key words: Fractal dimension, Cervical Cancer, Cytology, simulation, L-SIL.

INTRODUCCIÓN

El cáncer de cuello uterino es una patología que, mundialmente, causa la muerte a 275.000 mujeres al año. Para 2008, se reporta una incidencia anual en el globo de 530.000 casos nuevos. Más del 85% de esta casuística, se presenta en países en vías de desarrollo (WHO, 2008), siendo en el continente americano el cuarto tipo de cáncer más frecuente en mujeres, registrando, para 2008, en la zona de América Latina y el Caribe, 31.712 muertes, por esta causa (WHO/ ICO, 2010).

La citología cervico-vaginal ha sido considerada como el Gold-estándar para el tamizaje de cáncer de cuello uterino, por más de 50 años. Actualmente, el test citológico se encuentra fundamentado en parámetros cualitativos, motivo por el cual, se dificulta el establecimiento de un único sistema de clasificación de los estadios de alteración celular. El sistema de clasificación más ampliamente reconocido en el mundo es el Bethesda, que permite la identificación de lesiones precursoras, que pueden evolucionar hacia estadios de malignidad y ha establecido, con métodos cualitativos, la diferenciación de células normales, lesiones intraepiteliales de bajo o alto grado y células escamosas atípicas de significado indeterminado (ASCUS) (Lacruz, 2003).

Esta última clasificación es de gran relevancia, dado que pueden representar ambiguamente un proceso benigno o una lesión de riesgo y fue un término introducido, con el fin de obtener una mayor precisión de esa zona de gris de transición, entre la normalidad y la malignidad (Lacruz, 2003; Solomon et al. 2002).

La geometría fractal hizo su aparición gracias al cuestionamiento de la capacidad de la geometría euclidiana de poder establecer medidas objetivas y reproducibles de objetos irregulares de la naturaleza (Mandelbrot, 1967). Desde entonces, se han desarrollado aplicaciones a partir de la geometría fractal para el estudio de diversos objetos irregulares, tal como las estructuras anatómicas de sistemas vivos, como el humano, llegando a caracterizar estados de normalidad y enfermedad (Raguso et al. 2010; Rashidnasab et al. 2013; Xu et al. 2008). En el campo de la oncología, la geometría fractal ha sido utilizada en diversos estudios para caracterizar diversas formas cancerígenas (de Arruda et al. 2013; Klatt et al. 2013; Metze, 2013), como por ejemplo, para el estudio de diversas lesiones en imágenes mamográficas (Sankar & Thomas, 2010; Stępień & Stępień, 2010). Así como también ha sido de utilidad para la identificación del riesgo de diferentes tipos de cáncer (Stehlík et al. 2012) y para caracterizar los determinantes físicos del proceso de crecimiento tumoral, en general (Welter & Rieger, 2010); sin embargo, en algunos estudios, se ha venido demostrando que la medición de dimensiones fractales aisladas es insuficiente para establecer una caracterización matemática que pueda ser de aplicación clínica.

Con respecto a este problema, Rodríguez (2011a) desarrolló una metodología diagnóstica, que se basa en medidas de variabilidad y de la armonía matemática intrínseca celular para el estudio de lesiones pre-malignas, para superar la dificultad de la insuficiencia de aplicabilidad clínica de las dimensiones fractales aisladas, donde se demostró que la clasificación ASCUS (Atypical Squamous Cells of Undetermined Significance) puede ser aclarada. En un estudio llevado a cabo por el mismo grupo de investigación, se desarrolló una generalización de todos los posibles tipos celulares que incluyen desde estadios normales hasta lesiones malignas, a partir de la geometría fractal (Rodríguez et al. 2010a), logrando un diagnóstico objetivo y reproducible para cada caso específico independiente de variables estadísticas, fundamentado en formas de razonamiento universalistas. Trabajos similares se han desarrollado en arterias por medio de variaciones de la ocupación espacial de los objetos medidos en el espacio de Box-counting, encontrando en total 69,249 prototipos arteriales, entre anormales y normales (Rodríguez et al. 2010b).

Siguiendo esta misma metodología, se ha realizado una aplicación similar basada en geometría fractal (Rodríguez et al. 2013a), en la que se simulan las rutas de alteración de las células escamosas de cuello uterino, desde estados de normalidad hasta el estado denominado ASCUS, que en trabajos previos se había demostrado que podría corresponder según valores matemáticos a los estados de normalidad o Lesión Intraepitelial de Bajo Grado. Esto se realizó simulando variaciones geométricas para cada célula en el espacio de Box-counting para construir unas posibles trayectorias, desde la normalidad hasta ASCUS, a partir de una perspectiva acausal, obteniéndose resultados de utilidad para la práctica clínica cotidiana.

Siguiendo esta perspectiva de investigación, el propósito del presente estudio, fue analizar posibles rutas de alteración de las células escamosas de cuello uterino, también desde el estadio de la normalidad, pero esta vez hasta el estadio de LEIBG. Esto se realizó mediante simulaciones geométricas de la alteración celular en el espacio de Box Counting, evaluadas con el concepto de variabilidad fractal y AMI celular. Las simulaciones logradas constituyen una herramienta de apoyo en el seguimiento de pacientes con factores de riesgo para cáncer de cuello uterino, aclarando de nuevo el diag nóstico de ASCUS, aceptado convencionalmente en patología.

MATERIALES Y MÉTODOS

Se analizaron diez imágenes de células escamosas de cuello uterino obtenidas del archivo particular del grupo Insight, clasificadas como normales por un patólogo experto, de acuerdo con los parámetros de evaluación actual establecidos en el Sistema Bethesda. Las células fueron inicialmente fotografiadas con cámara digital Nikon, adaptada a un microscopio Nikon Eclipse ε200, utilizando un aumento de 100X. Luego, fueron importadas a una aplicación que edita imágenes, para facilitar su análisis ulterior.

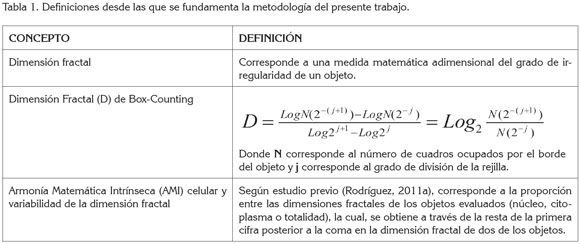
El análisis de las imágenes, se basó en el cálculo de la dimensión fractal del borde de la membrana celular (C), nuclear (N) y de la totalidad celular, utilizando una simplificación del método de Box-Counting, en el que se usan sólo dos rejillas (Tabla 1).

Para el cálculo de la dimensión fractal, se superponen dos rejillas sobre las imágenes celulares, donde el lado de una corresponde exactamente al doble del lado de la segunda. Luego, se contabilizan los cuadros que son tocados por los bordes de cada uno de los objetos, valores que se reemplazan en la ecuación de Box-counting (Tabla 1).

Posteriormente, las dimensiones fractales de estos tres objetos fueron comparadas en pares, mediante las medidas de AMI celular y la variabilidad fractal (Rodríguez, 2011a). De este modo, se obtuvieron comparaciones entre Nucleo y Citoplasma, Nucleo y Totalidad y Citoplasma y Totalidad.

Seguidamente, se desarrollaron tres simulaciones de las posibles variaciones de la ocupación espacial de los objetos celulares, definidos para cada célula estudiada (Nucleo, Citoplasma y Totalidad), estableciendo así una ruta de alteración entre normalidad y LEIBG, para cada célula. Así, por ejemplo, si en la célula original el núcleo ocupa 10 espacios en una de las rejillas es posible hacer simulaciones en las que ocupe 11, 12 o más pixeles, lo que implica variaciones en la ocupación espacial de la otra rejilla.

De acuerdo con la metodología diagnóstica en la que se basa el presente trabajo, la clasificación ASCUS no presenta características matemáticas que la diferencien de normalidad o de L-SIL, sino que puede tomar valores análogos a uno u otro estado (Rodríguez, 2011a). Con el fin de confirmar si las simulaciones incluyen células que puedan ser consideradas ASCUS, las células simuladas fueron observadas por un experto en patología, quien de acuerdo con la observación de sus características morfológicas desde los parámetros convencionales, estableció su diagnóstico.

RESULTADOS Y DISCUSIÓN

Este es el primer trabajo en el que se desarrollan las posibles rutas de alteración de 10 células normales hacia una célula clasificada como LEIBG, fundamentadas en el concepto de AMI celular y variabilidad de la dimensión fractal, obteniendo un resultado que puede ser útil como herramienta de tamizaje para la detección temprana de alteraciones, que pueden conducir hacia lesión maligna en el cuello uterino, al permitir determinar cuándo, por ejemplo, una célula clasificada como ASCUS, se encuentra más cerca de un estado de normalidad o un estado de LEIBG. La metodología presentada en este trabajo puede ser de utilidad para poder determinar cuándo una célula clasificada como ASCUS se encuentra más cerca de un estado de normalidad o un estado de LEIBG.

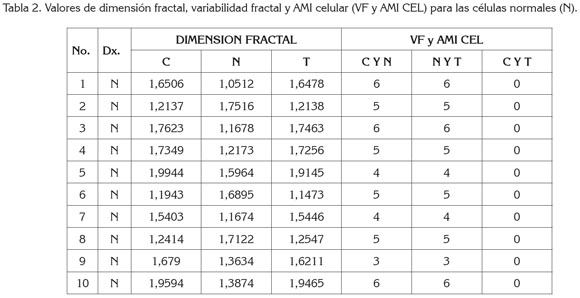
Los valores de la dimensión fractal del borde celular de las células normales variaron entre 1,9944 y 1,1943; para el borde nuclear varió entre 1,7516 y 1,0512 y para la totalidad celular, se halló entre 1,9465 y 1,1473. Al calcular los valores correspondientes de AMI celular y variabilidad fractal, se halló que al comparar las medidas de citoplasma y núcleo se registraron valores entre tres y seis, rango que comparte con los valores de la comparación entre núcleo y totalidad, mientras que la comparación entre citoplasma y totalidad fue de cero para todas las células normales (Tabla 2).

Respecto a los valores de las simulaciones realizadas, se encontraron valores de dimensión fractal entre 1,9594 y 0,3725, para el citoplasma; para el núcleo, entre 1,9216 y 0,3461, mientras que para la totalidad se registraron entre 1,8168 y 0,3863 (Tablas 3, 4y 5). Con respecto a las medidas de AMI y variabilidad, los valores hallados entre Citoplasma y Núcleo variaron entre 0 y 6; los valores entre Núcleo y Totalidad, entre 0 y cinco y entre el citoplasma y la totalidad, entre 0 y 2.

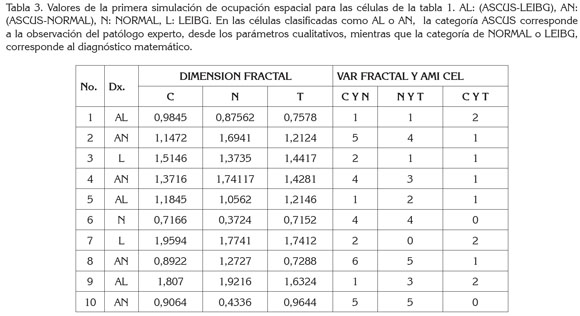
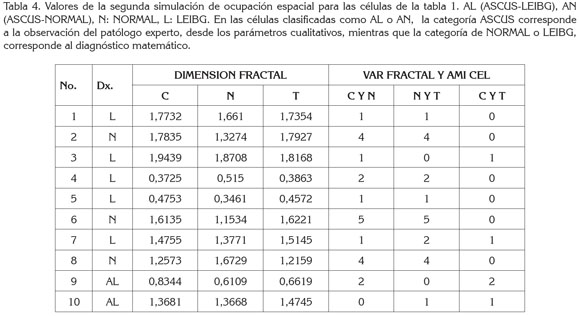
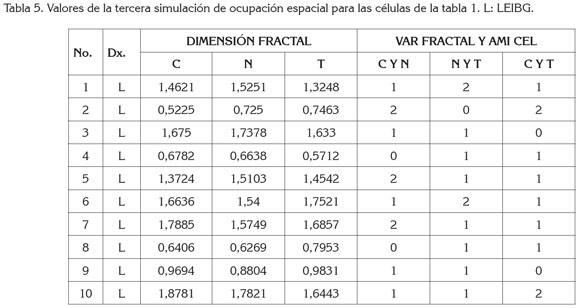
Con la primera simulación teórica, se obtuvieron cinco células, cuyos valores matemáticos de AMI y de variabilidad corresponden a normalidad, de las cuales, cuatro fueron catalogadas por un experto patólogo, como ASCUS. Las demás células tuvieron valores matemáticos de LEIBG, donde tres fueron catalogadas como ASCUS. En la segunda simulación, se obtuvieron tres células con valores matemáticos de normalidad, las siete restantes con valores correspondientes a LEIBG, haciendo notar que, de estas últimas, dos fueron catalogadas como ASCUS, por el patólogo. Finalmente, en la tercera simulación, se obtuvieron células con valores matemáticos de AMI y de variabilidad, que son característicos del estado LEIBG (Tablas 3, 4y 5).

La evaluación realizada por el patólogo de las células simuladas evidencia que la metodología permite simular y establecer un diagnóstico objetivo de células que, desde los parámetros convencionales, son clasificadas como ASCUS y confirma que el estadio correspondiente a la clasificación patológica de ASCUS no tiene un sustento matemático, ya que no tiene valores característicos que se asocien a esta categoría, tal como sí sucede con el estadio de normalidad y LEIBG.

Tal como se viene manejando el tamizaje, a través la citología cervicovaginal para detección precoz de lesiones malignas en cuello uterino, el sistema Bethesda, aparte de las clasificaciones de normalidad y lesión intraepitelial, ofrece una clasificación que constituye una "zona gris" indeterminada, que representa un problema para la toma de decisiones clínicas, al no poder extraerse de dicha clasificación un diagnóstico concluyente ni una conducta específica. El estudio de las rutas posibles que puede tomar una célula normal hacia una clasificada como LEIBG es de gran relevancia para el desarrollo de herramientas más precisas de tamizaje y que permitan predecir el posible desenlace, a partir de una forma celular específica. Por otro lado, dado que se trata de una metodología basada en la geometría, la aplicación futura de esta herramienta, para predicción de posibles desenlaces relacionados con procesos neoplásicos, superaría la dificultad inherente a las clasificaciones cualitativas de la alta variabilidad interobservador, ya que las medidas cuantitativas ofrecen la ventaja de ser objetivas y reproducibles.

Esta metodología evidencia que el fenómeno puede ser estudiado de manera más efectiva haciendo abstracción de factores individuales y poblacionales y hallando órdenes matemáticos acausales subyacentes, que permitan realizar aplicaciones en el ámbito clínico, útiles para identificar, de manera precisa, aquellos casos que presentan mayor probabilidad de tener valores cercanos a Lesiones Intraepiteliales. Desde esta postura acausal, diversas metodologías diagnósticas y predictivas se han desarrollado aplicando diferentes teorías físicas y matemáticas en áreas de la medicina, tales como la salud pública (Rodríguez, 2010), la biología molecular (Rodríguez et al. 2009, 2010c), la cardiología (Rodríguez, 2011b, Rodríguez et al. 2013c), la hematología (Correa et al. 2012) y la infectología (Rodríguez et al. 2013b).

Agradecimientos:

BIBLIOGRAFÍA

1. CORREA, C.; RODRÍGUEZ, J.; PRIETO, S.; BERNAL, P.; OSPINO, B.; MUNÉVAR, A.; ÁLVAREZ, L.; MORA, J.; VITERY, S. 2012. Geometric diagnosis of erythrocyte morphophysiology. J. Med. Med. Sci. (Nigeria). 3(11):715-720.

2. DE ARRUDA, P.F.F.; GATTI, M.; FACIO, F.N. JR.; DE ARRUDA, J.G.F.; MOREIRA, R.D.; MURTA, L.O. JR; DE ARRUDA, L.F.; DE GODOY, M.F. 2013. Quantification of fractal dimension and Shannon's entropy in histological diagnosis of prostate cancer. BMC clinical pathology. (Reino Unido) 13(1):6.

3. KLATT, J.; GERICH, C.E.; GRÖBE, A.; OPITZ, J.; SCHREIBER, J.; HANKEN, H.; SALOMON, G.; HEILAND, M.; KLUWE, L.; BLESSMANN, M. 2013. Fractal dimension of time-resolved autofluorescence discriminates tumour from healthy tissues in the oral cavity. J. Cranio-Maxillofacial Surg. (Europa). 13(7):719-735.

4. LACRUZ, C. 2003. Nomenclatura de las lesiones cervicales (de Papanicolau a Bethesda 2001). Rev. Esp. Patol. (España) 36(1):5-10.

5. MANDELBROT, B. 1967. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science, New Series (Estados Unidos) 156(3775):636-638.

6. METZE, K. 2013. Fractal dimension of chromatin: potential molecular diagnostic applications for cancer prognosis. Expert Rev. Mol. Diagn. (Reino Unido) 13(7):719-35.

7. RAGUSO, G.; ANCONA, A.; CHIEPPA, L.; L'ABBATE, S.; PEPE, M.L.; MANGIERI, F.; DE PALO, M.; RANGAYYAN, R.M. 2010. Application of fractal analysis to mammography. In: Engineering in Medicine and Biology Society (EMBC), 2010 Annual International Conference of the IEEE. (Argentina). p.3182-3185.

8. RASHIDNASAB, A.; ELANGOVAN, P.; YIP, M.; DIAZ, O.; DANCE, D.R.; YOUNG, K.C.; WELLS, K. 2013. Simulation and assessment of realistic breast lesions using fractal growth models. Physics in Medicine and Biology. (Canada). 58(16):5613-5627.

9. RODRÍGUEZ, J.; BERNAL, P.; CORREA, C.; PRIETO, S.; BENÍTEZ, L.; VITERY, S.; PUERTA, G.; MUÑOZ, D.; ROJAS, I.; SORACIPA, Y. 2009. Predicción de unión de péptidos de MSA-2 y AMA-1 de Plasmodium falciparum al HLA clase II. Inmunol. (España) 28(3):115 124.

10. RODRÍGUEZ, J. 2010. Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev. Panam. Salud Públ. (Colombia). 27(3):211-218.

11. RODRÍGUEZ, J. 2011a. Nuevo método fractal de ayuda diagnóstica para células preneoplásicas del epitelio escamoso cervical. Rev. U.D.C.A Act. & Div. Cient. (Colombia). 14(1):15-22.

12. RODRÍGUEZ, J. 2011b. Mathematical law of chaotic cardiac dynamics: Predictions for clinical application. J. Med. Med. Sci (Nigeria). 2(8):1050-1059.

13. RODRÍGUEZ, J.; PRIETO, S.; CORREA, C.; POSSO, H.; BERNAL, P.; PUERTA, G.; VITERY, S.; ROJAS, I. 2010a. Generalización fractal de células preneoplásicas y cancerígenas del epitelio escamoso cervical. Una nueva metodología de aplicación clínica. Rev. Fac. Med. (Colombia). 18(2):173-181.

14. RODRÍGUEZ, J.; PRIETO, S.; CORREA, C.; BERNAL, P.; PUERTA, G.; VITERY, S.; SORACIPA, Y.; MUÑOZ D. 2010b. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Med. Phys. (Inglaterra). 10:1-6.

15. RODRÍGUEZ, J.; BERNAL, P.; PRIETO, S.; CORREA, C. 2010c. Teoría de péptidos de alta unión de malaria al glóbulo rojo. Predicciones teóricas de nuevos péptidos de unión y mutaciones teóricas predictivas de aminoácidos críticos. Inmunol. (España) 29(1):7-19.

16. RODRÍGUEZ, J.; PRIETO, S.; TABARES, L.; RUBIANO, A.; PRIETO, I.; DOMÍNGUEZ, D.; PATIÑO, O.; MEJÍA, M.; RAMÍREZ, L. 2013a. Evolución de células de cuello uterino desde normales hasta atipias escamosas de significado indeterminado (ASCUS) con geometría fractal. Rev. U.D.C.A Act. & Div. Cient. (Colombia). 16(2):303-311.

17. RODRÍGUEZ, J.; PRIETO, S.; CORREA, C.; FORERO, M.F.; PÉREZ, C.; SORACIPA, Y.; MORA, J.; ROJAS, N.; PINEDA, D.; LÓPEZ, F. 2013b. Teoría de conjuntos aplicada al recuento de linfocitos y leucocitos: predicción de linfocitos T CD4 de pacientes con virus de la inmunodeficiencia humana/sida. Inmunol. (España) 32(2):50-56.

18. RODRÍGUEZ, J.; PRIETO, S.; DOMÍNGUEZ, D.; MELO, M,; MENDOZA, F.; CORREA, C.; SORACIPA, Y.; PINILLA, L.; PARDO, J.; RAMÍREZ, N. 2013c. Mathematical-physical prediction of cardiac dynamics using the proportional entropy of dynamic systems. J. Med. Med. Sci. (Nigeria) 4(8):370-381.

19. SANKAR, D.; THOMAS, T. 2010. A New Fast Fractal Modeling Approach for the Detection of Microcalcifications in Mammograms. J. Digit. Imaging. (Estados Unidos). 23(5):538-546.

20. SOLOMON, D.; DAVEY, D.; KURMAN, R.; MORIARTY, A.; O'CONNOR, D.; PREY, M.; RAAB, S.; SHERMAN, M.; WILBUR, D.; WRIGHT, T.J.; YOUNG, N. 2002. The 2001 Bethesda System. JAMA (Estados Unidos). 287:2114-2119.

21. STEHLÍK, M.; MRKVICKA, T.; FILUS, J.; FILUS, L. 2012. Recent developments on testing in cancer risk: a fractal and stochastic geometry. J. Reliab. Statist. Studi. (India). 5(Issue Special):83-95.

22. STEPIEŃ, R.; STEPIEŃ, P. 2010. Analysis of Contours of Tumor Masses in Mammograms by Higuchi's Fractal Dimension. Biocybern. Biomed. Eng. (Polonia). 30(4):49-56.

23. WELTER, M.; RIEGER, H. 2010. Physical determinants of vascular network remodeling during tumor growth. Eur. Phys. J. E. (Francia). 33:149-163.

24. WHO/ICO. Information Centre on HPV and Cervical Cancer (HPV Information Centre). 2010. Human Papillomavirus and Related Cancers in Americas. Summary Report 2010. Disponible desde Internet en: http://www.who.int/hpvcentre (Con acceso 01/11/2012).

25. WORLD HEALTH ORGANIZATION. International Agency for Research Center. Globocan. 2008. Fact Sheets: Cervix uteri, Worldwide. Disponible desde Internet en: http://globocan.iarc.fr/factsheet.asp (con acceso 14/01/2013).

26. XU, M.; WU, T.T.; QU, J.Y. 2008. Unified Mie and fractal scattering by cells and experimental study on application in optical characterization of cellular and subcellular structures. J. Biomed. Optics. (Estados Unidos) 13(2):024015.

Recibido: Agosto 9 de 2013 Aceptado: Febrero 10 de 2014